diff --git a/docs/ce1/math117.md b/docs/ce1/math117.md
index 12cb031..3e03e37 100644
--- a/docs/ce1/math117.md
+++ b/docs/ce1/math117.md
@@ -1 +1,72 @@
-# MATH 117: Calculus for Engineering
+# MATH 117: Calculus 1
+
+## Functions
+
+A **function** is a rule where each input has exactly one output, which can be determined by the **vertical line test**.
+
+!!! definition
+ - The **domain** is the set of allowable independent values.
+ - The **range** is the set of allowable dependent values.
+
+Functions can be **composed** to apply the result of one function to another.
+$$
+(f\circ g)(x) = f(g(x))
+$$
+
+!!! warning
+ Composition is not commutative: $f\circ g \neq g\circ f$.
+
+## Inverse functions
+
+The inverse of a function swaps the domain and range of the original function: $f^{-1}(x)$ is the inverse of $f(x)$.. It can be determined by solving for the other variable:
+$$
+\begin{align*}
+y&=mx+b \\
+y-b&=mx \\
+x&=\frac{y-b}{m}
+\end{align*}
+$$
+
+Because the domain and range are simply swapped, the inverse function is just the original function reflected across the line $y=x$.
+
+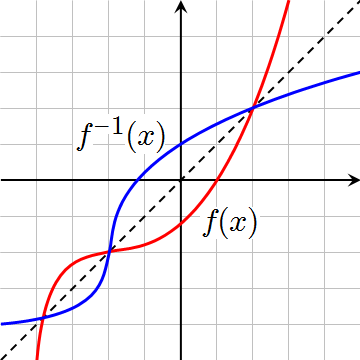 (Source: Wikimedia Commons, public domain)
+
+If the inverse of a function is applied to the original function, the original value is returned.
+$$f^{-1}(f(x)) = x$$
+
+A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
+
+If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
+
+!!! example
+
(Source: Wikimedia Commons, public domain)
+
+If the inverse of a function is applied to the original function, the original value is returned.
+$$f^{-1}(f(x)) = x$$
+
+A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
+
+If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
+
+!!! example
+  (Source: Wikimedia Commons, public domain)
+ By restricting the domain to $[0,\inf]$, the **multivalued inverse function** $y=\pm\sqrt{x}$ is reduced to just the partial inverse $y=\sqrt{x}$.
+
+## Symmetry
+
+An **even function** satisfies the property that $f(x)=f(-x)$, indicating that it is unchanged by a reflection across the y-axis.
+
+An **odd function** satisfies the property that $-f(x)=f(-x)$, indicating that it is unchanged by a 180° rotation about the origin.
+
+The following properties are always true for even and odd functions:
+
+ - even × even = even
+ - odd × odd = even
+ - even × odd = odd
+
+Functions that are symmetric (that is, both $f(x)$ and $f(-x)$ exist) can be split into an even and odd component. Where $g(x)$ is the even component and $h(x)$ is the odd component:
+$$
+\begin{align*}
+f(x) &= g(x) + h(x) \\
+g(x) &= \frac{1}{2}(f(x) + f(-x)) \\
+h(x) &= \frac{1}{2}(f(x) - f(-x))
+\end{align*}
+$$
+
+!!! note
+ The hyperbolic sine and cosine are the even and odd components of $f(x)=e^x$.
+ $$
+ \cosh x = \frac{1}{2}(e^x + e^{-x}) \\
+ \sinh x = \frac{1}{2}(e^x - e^{-x})
+ $$
+
(Source: Wikimedia Commons, public domain)
+ By restricting the domain to $[0,\inf]$, the **multivalued inverse function** $y=\pm\sqrt{x}$ is reduced to just the partial inverse $y=\sqrt{x}$.
+
+## Symmetry
+
+An **even function** satisfies the property that $f(x)=f(-x)$, indicating that it is unchanged by a reflection across the y-axis.
+
+An **odd function** satisfies the property that $-f(x)=f(-x)$, indicating that it is unchanged by a 180° rotation about the origin.
+
+The following properties are always true for even and odd functions:
+
+ - even × even = even
+ - odd × odd = even
+ - even × odd = odd
+
+Functions that are symmetric (that is, both $f(x)$ and $f(-x)$ exist) can be split into an even and odd component. Where $g(x)$ is the even component and $h(x)$ is the odd component:
+$$
+\begin{align*}
+f(x) &= g(x) + h(x) \\
+g(x) &= \frac{1}{2}(f(x) + f(-x)) \\
+h(x) &= \frac{1}{2}(f(x) - f(-x))
+\end{align*}
+$$
+
+!!! note
+ The hyperbolic sine and cosine are the even and odd components of $f(x)=e^x$.
+ $$
+ \cosh x = \frac{1}{2}(e^x + e^{-x}) \\
+ \sinh x = \frac{1}{2}(e^x - e^{-x})
+ $$
+
 (Source: Wikimedia Commons, public domain)
+
+If the inverse of a function is applied to the original function, the original value is returned.
+$$f^{-1}(f(x)) = x$$
+
+A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
+
+If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
+
+!!! example
+
(Source: Wikimedia Commons, public domain)
+
+If the inverse of a function is applied to the original function, the original value is returned.
+$$f^{-1}(f(x)) = x$$
+
+A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
+
+If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
+
+!!! example
+