# ECE 124: Digital Circuits
## Base / radix conversion
Please see [ECE 150: C++#Non-decimal numbers](/1a/ece150/#non-decimal numbers) for more information.
## Binary logic
A **binary logic variable** is a variable that has exactly two states:
- 0, or false (switch open)
- 1, or true (switch closed)
**Binary logic functions** are any function that satisfies the following type signature:
```python
BoolFunc = Callable[[bool | BoolFunc, ...], bool]
```
In other words:
- it must accept a number of booleans and/or other logic functions, and
- it must return exactly one boolean.
These can be expressed via truth table inputs/outputs, algebraically, or via a logical circuit schematic.
### Logical operators
Operator precedence is () > NOT > AND > OR.
The **AND** operator returns true if and only if **all** arguments are true.
$$A\cdot B \text{ or }AB$$
(Source: Wikimedia Commons)
The **OR** operator returns true if and only if **at least one** argument is true.
$$A+B$$
(Source: Wikimedia Commons)
The **NOT** operator returns the opposite of its singular input.
$$\overline A \text{ or } A'$$
(Source: Wikimedia Commons)
### Postulates
In binary algebra, if $x,y,z\in\mathbb B$ such that $\mathbb B=\{0, 1\}$:
The **identity element** for **AND** $1$ is such that any $x\cdot 1 = x$.
The **identity element** for **OR** $0$ is such that any $x + 0 = x$.
In this space, it can be deduced that $x+x'=1$ and $x\cdot x'=0$.
**De Morgan's laws** are much easier to express in boolean algebra, and denote distributing a negation by flipping the operator:
$$
(x\cdot y)'=x'+y' \\
(x+y)=x'\cdot y'
$$
Please see [ECE 108: Discrete Math 1#Operator laws](/1b/ece108/#operator-laws) for more information.
AND and OR are commutative.
- $x\cdot y=y\cdot x$
- $x+y=y+x$
AND and OR are associative.
- $x\cdot(y\cdot z)=(x\cdot y)\cdot z)$
- ...
AND and OR are distributive with each other.
- $x\cdot (y+z)=x\cdot y+z\cdot z$
A term that depends on another term ORed together can be "absorbed".
- $x+x\cdot y=x$
- $x\cdot(x+y)=x$
If a term being true also results in other ORed terms being true, it is redundant and can be eliminated via consensus.
- $x\cdot y+y\cdot z+x'\cdot z=x\cdot y+x'\cdot z$
- if y and z are true, at least one of the other two terms must be true
- $(x+y)\cdot (y+z)\cdot(x'+z)=(x+y)\cdot (x'+z)$
The **synthesis** of an algebraic formula represents its implementation via logic gates. In this course, its total cost is the sum of all inputs to all gates and the number of gates, *excluding* initial inputs of "true" or an initial negation.
In order to deduce an algebraic expression from a truth table, **OR** all of the rows in which the function returns true and simplify.
??? example
Prove that $(x+y)\cdot(x+y')=x$:
\begin{align*}
\tag{distributive property}(x+y)\cdot(x+y')&=xx+xy'+yx+yy' \\
\tag{$yy'$ = 0, $xx=x$}&=x + xy' + yx \\
\tag{distributive, commutative properties}&= x(1+y'+y) \\
\tag{1 + ... = 1}&= x(1) \\
&=x
\end{align*}
Prove that $xy+yz+x'z=xy+x'z$:
\begin{align*}
\tag{$x+x'=1$}xy+yz+x'z&=xy+yz(x+x')+x'z \\
\tag{distributive property}&=xy+xyz+x'yz+x'z \\
\tag{distributive property}&=x(y+yz) + x'(yz+z) \\
\tag{distributive property}&=xy(1+z) + x'z(y+1) \\
\tag{$1+k=1$}&=xy(1) + x'z(1) \\
\tag{$1\cdot k=k$}&= xy+x'z
\end{align*}
### Minterms and maxterms
The **minterm** $m$ is a **product** term where all variables in the function appear once. There are $2^n$ minterms for each function, where $n$ is the number of input variables.
To determine the relevant function, the subscript can be converted to binary and each function variable set such that:
- if the digit is $1$, the complement is used, and
- if the digit is $0$, the original is used.
$$m_j=x_1+x_2+\dots x_n$$
!!! example
For a function that accepts three variables:
- there are eight minterms, from $m_0$ to $m_7$.
- the sixth minterm $m_6=xyz'$ because $6=0b110$.
For a sample function defined by the following minterms:
$$
\begin{align*}
f(x_1,x_2,x_3)&=\sum m(1,2,5) \\
&=m_1+m_2+m_5 \\
&=x_1x_2x_3' + x_1x_2'x_3 + x_1'x_2x_3'
\end{align*}
$$
The **maxterm** $M$ is a **sum** term where all variables in the function appear once. It is more or less the same as a minterm, except the condition for each variable is **reversed** (i.e., $0$ indicates the complement).
$$M_j=x_1+x_2+\dots +x_n$$
!!! example
For a sample function defined by the following maxterms:
\begin{align*}
f(x_1,x_2,x_3,x_4)&=\prod M(1,2,8,12) \\
&=M_1M_2M_8M_{12} \\
\end{align*}
??? example
Prove that $\sum m(1,2,3,4,5,6,7)=x_1+x_2+x_3$: **(some shortcuts taken for visual clarity)**
\begin{align*}
\sum m(1,2,3,4,5,6,7) &=001+011+111+010+110+100+000 \\
\tag{SIMD distribution}&=001+010+100 \\
&=x_1+x_2+x_3
\end{align*}
A **canonical sum of products (SOP)** is a function expressed as a sum of minterms.
$$f(x_1,x_2,\dots)=\sum m(a,b, \dots)$$
A **canonical product of sums (POS)** is a function expressed as a product of maxterms.
$$f(x_1,x_2,\dots)=\prod M(a,b,\dots)$$
## VHDL
VHDL is a hardware schematic language.
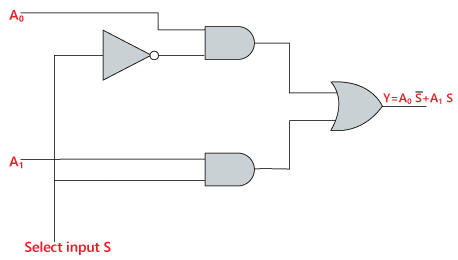For example, the basic 2-to-1 multiplexer expressed above can be programmed as:
```vhdl
entity two_one_mux is
port (a0, s, a1 : in bit;
f : out bit);
end two_one_mux
architecture LogicFunc of two_one_mux is
begin
y <= (a0 AND s) OR (NOT s AND a1);
end LogicFunc;
```
In this case, the inputs are `a0, s, a1` that lead to an output `y`. All input/output is of type `bit` (a boolean).
The **architecture** defines how inputs translate to outputs via functions. These all run **concurrently**.