# ECE 240: Electronic Circuits
## Diodes
A **diode** is a two-terminal device that only allows current to flow in the direction of the arrow.
(Source: Wikimedia Commons)
The current across a diode is, where $I_s$ is a forced saturation current, $V$ is the voltage drop across it, and $V_T$ is the **thermal voltage** such that $V_T=\frac{kT}{q}$, where $T$ is the temperature, $k$ is the Boltzmann constant, and $q$ is the charge of an electron:
$$I=I_s\left(e^{V/V_T}-1\right)$$
!!! tip
- $V_T\approx\pu{25 mV}$ at 20°C
- $V_T\approx\pu{20 mV}$ at 25°C
A diode is open when current is flowing reverse the desired direction, resulting in zero current, until the voltage drop becomes so great that it reaches the **breakdown voltage** $V_B$. Otherwise, the above current formula is followed.
(Source: Wikimedia Commons)
Diodes are commonly used in **rectifier circuits** — circuits that convert AC to DC.
By preventing negative voltage, a relatively constant positive DC voltage is obtained. The slight dip between each hill is known as **ripple** $\Delta V$.
(Source: Wikimedia Commons)
In a simple series RC circuit, across a diode, Where $R_LC>>\frac 1 \omega$, and $f=\frac{\omega}{2\pi}$:
$$\Delta V\approx \frac{I_\text{load}}{2fC}\approx\frac{V_0}{2fR_LC}$$
### Zener diodes
A Zener diode is a calibrated diode with a known breakdown voltage, $V_B$. If the voltage across the diode would be greater than $V_B$, it is **capped at $V_B$.**
(Source: Wikimedia Commons)
## Voltage/current biasing
Solving for current for each element in a series returns a negative linear line and other non-linear lines.
- the linear line is the **load line**, which represents the possible solutions to the circuit when it is loaded
- Depending on the base current $I_s$, the diode or transistor will be **biased** toward one of the curves, and the voltage and current will settle on one of the intersections, or **bias points**.
(Source: Wikimedia Commons)
- To bias current, as $R\to\infty$ (or, in practical terms, $R>>diode$), the slope of the load line $\to 0$, which results in a constant current.
- To bias voltage, as $R\to 0$, the slope of the load line $\to\infty$, which results in a constant voltage.
!!! example
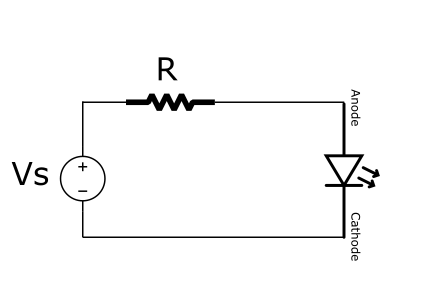The current across the resistor and the diode is the same:
\begin{align*}
i_D&=\frac{V_s}{R} \\
i_D&\approx I_se^{V_D/V_T}
\end{align*}
If a diode is put in series with AC and DC voltage sources $V_d(t)$ and $V_D$:
\begin{align*}
i_D(t)&=I_se^{(V_D+V_d(t))/V_T} \\
&=\underbrace{I_se^{V_D/V_T}}_\text{bias current}\ \underbrace{e^{V_d(t)/V_T}}_\text{$\approx 1+\frac{V_d}{V_T}$} \\
&=I_D\left(1+\frac{V_d}{V_T}\right) \\
&=\underbrace{I_D}_\text{large signal = bias = DC}+\underbrace{I_D\frac{V_d(t)}{V_T}}_\text{small signal = AC}
\end{align*}
Diodes may act as resistors, depending on the bias current. They may exhibit a **differential resistance**:
$$r_d=\left(\frac{\partial i_D}{\partial v_D}\right)^{-1} = \frac{V_T}{I_D}$$
!!! example
Thus from the previous sequence:
$$i_D(t)=I_D+\frac{1}{r_d}V_d(t)$$
### Signal analysis
1. Analyse DC signals
- assume blocking capacitors are open circuits
- turn off AC sources
2. Analyse AC signals
- assume blocking capacitors are shorts
- turn off DC sources
- replace diode with effective resistor (the differential resistor)
!!! tip
Most $R$s in the circuit can be assumed to be significantly greater than $r_d$, so $r_d$ can be removed in series or $R$ can be removed in parallel.
!!! warning
Oftentimes, turning off a DC source to nowhere is actually a short to ground.