# ECE 124: Digital Circuits
## Base / radix conversion
Please see [ECE 150: C++#Non-decimal numbers](/1a/ece150/#non-decimal numbers) for more information.
## Binary logic
A **binary logic variable** is a variable that has exactly two states:
- 0, or false (switch open)
- 1, or true (switch closed)
**Binary logic functions** are any function that satisfies the following type signature:
```python
BoolFunc = Callable[[bool | BoolFunc, ...], bool]
```
In other words:
- it must accept a number of booleans and/or other logic functions, and
- it must return exactly one boolean.
These can be expressed via truth table inputs/outputs, algebraically, or via a logical circuit schematic.
### Logical operators
Operator precedence is () > NOT > AND > OR.
The **AND** operator returns true if and only if **all** arguments are true.
$$A\cdot B \text{ or }AB$$
 (Source: Wikimedia Commons)
The **OR** operator returns true if and only if **at least one** argument is true.
$$A+B$$
(Source: Wikimedia Commons)
The **OR** operator returns true if and only if **at least one** argument is true.
$$A+B$$
 (Source: Wikimedia Commons)
The **NOT** operator returns the opposite of its singular input.
$$\overline A \text{ or } A'$$
(Source: Wikimedia Commons)
The **NOT** operator returns the opposite of its singular input.
$$\overline A \text{ or } A'$$
 (Source: Wikimedia Commons)
The **NAND** operator is equivalent to **NOT AND**.
$$\overline{A\cdot B}$$
(Source: Wikimedia Commons)
The **NAND** operator is equivalent to **NOT AND**.
$$\overline{A\cdot B}$$
 (Source: Wikimedia Commons)
The **NOR** operator is equivalent to **NOT OR**.
$$\overline{A+B}$$
(Source: Wikimedia Commons)
The **NOR** operator is equivalent to **NOT OR**.
$$\overline{A+B}$$
 (Source: Wikimedia Commons)
### NAND/NOR completeness
NAND and NOR are **universal gates** — some combination of them can form any other logic gate. Constructions of other gates using only these gates are called **NAND-NAND realisations** or **NOR-NOR realisations**.
This is useful in SOP as if two ANDs feed into an OR, all can be turned into NANDs to achieve the same result.
!!! example
NOT can be expressed purely with NAND as $A$ NAND $A$:
(Source: Wikimedia Commons)
### NAND/NOR completeness
NAND and NOR are **universal gates** — some combination of them can form any other logic gate. Constructions of other gates using only these gates are called **NAND-NAND realisations** or **NOR-NOR realisations**.
This is useful in SOP as if two ANDs feed into an OR, all can be turned into NANDs to achieve the same result.
!!! example
NOT can be expressed purely with NAND as $A$ NAND $A$:
 (Source: Wikimedia Commons)
### Postulates
In binary algebra, if $x,y,z\in\mathbb B$ such that $\mathbb B=\{0, 1\}$:
The **identity element** for **AND** $1$ is such that any $x\cdot 1 = x$.
The **identity element** for **OR** $0$ is such that any $x + 0 = x$.
In this space, it can be deduced that $x+x'=1$ and $x\cdot x'=0$.
**De Morgan's laws** are much easier to express in boolean algebra, and denote distributing a negation by flipping the operator:
$$
(x\cdot y)'=x'+y' \\
(x+y)=x'\cdot y'
$$
Please see [ECE 108: Discrete Math 1#Operator laws](/1b/ece108/#operator-laws) for more information.
AND and OR are commutative.
- $x\cdot y=y\cdot x$
- $x+y=y+x$
AND and OR are associative.
- $x\cdot(y\cdot z)=(x\cdot y)\cdot z)$
- ...
AND and OR are distributive with each other.
- $x\cdot (y+z)=x\cdot y+z\cdot z$
A term that depends on another term ORed together can be "absorbed".
- $x+x\cdot y=x$
- $x\cdot(x+y)=x$
If a term being true also results in other ORed terms being true, it is redundant and can be eliminated via consensus.
- $x\cdot y+y\cdot z+x'\cdot z=x\cdot y+x'\cdot z$
- if y and z are true, at least one of the other two terms must be true
- $(x+y)\cdot (y+z)\cdot(x'+z)=(x+y)\cdot (x'+z)$
The **synthesis** of an algebraic formula represents its implementation via logic gates. In this course, its total cost is the sum of all inputs to all gates and the number of gates, *excluding* initial inputs of "true" or an initial negation.
In order to deduce an algebraic expression from a truth table, **OR** all of the rows in which the function returns true and simplify.
??? example
Prove that $(x+y)\cdot(x+y')=x$:
\begin{align*}
\tag{distributive property}(x+y)\cdot(x+y')&=xx+xy'+yx+yy' \\
\tag{$yy'$ = 0, $xx=x$}&=x + xy' + yx \\
\tag{distributive, commutative properties}&= x(1+y'+y) \\
\tag{1 + ... = 1}&= x(1) \\
&=x
\end{align*}
Prove that $xy+yz+x'z=xy+x'z$:
\begin{align*}
\tag{$x+x'=1$}xy+yz+x'z&=xy+yz(x+x')+x'z \\
\tag{distributive property}&=xy+xyz+x'yz+x'z \\
\tag{distributive property}&=x(y+yz) + x'(yz+z) \\
\tag{distributive property}&=xy(1+z) + x'z(y+1) \\
\tag{$1+k=1$}&=xy(1) + x'z(1) \\
\tag{$1\cdot k=k$}&= xy+x'z
\end{align*}
### Minterms and maxterms
The **minterm** $m$ is a **product** term where all variables in the function appear once. There are $2^n$ minterms for each function, where $n$ is the number of input variables.
To determine the relevant function, the subscript can be converted to binary and each function variable set such that:
- if the digit is $1$, the complement is used, and
- if the digit is $0$, the original is used.
$$m_j=x_1+x_2+\dots x_n$$
!!! example
For a function that accepts three variables:
- there are eight minterms, from $m_0$ to $m_7$.
- the sixth minterm $m_6=xyz'$ because $6=0b110$.
For a sample function defined by the following minterms:
$$
\begin{align*}
f(x_1,x_2,x_3)&=\sum m(1,2,5) \\
&=m_1+m_2+m_5 \\
&=x_1x_2x_3' + x_1x_2'x_3 + x_1'x_2x_3'
\end{align*}
$$
The **maxterm** $M$ is a **sum** term where all variables in the function appear once. It is more or less the same as a minterm, except the condition for each variable is **reversed** (i.e., $0$ indicates the complement).
$$M_j=x_1+x_2+\dots +x_n$$
!!! example
For a sample function defined by the following maxterms:
\begin{align*}
f(x_1,x_2,x_3,x_4)&=\prod M(1,2,8,12) \\
&=M_1M_2M_8M_{12} \\
\end{align*}
??? example
Prove that $\sum m(1,2,3,4,5,6,7)=x_1+x_2+x_3$: **(some shortcuts taken for visual clarity)**
\begin{align*}
\sum m(1,2,3,4,5,6,7) &=001+011+111+010+110+100+000 \\
\tag{SIMD distribution}&=001+010+100 \\
&=x_1+x_2+x_3
\end{align*}
A **canonical sum of products (SOP)** is a function expressed as a sum of minterms.
$$f(x_1,x_2,\dots)=\sum m(a,b, \dots)$$
A **canonical product of sums (POS)** is a function expressed as a product of maxterms.
$$f(x_1,x_2,\dots)=\prod M(a,b,\dots)$$
## VHDL
VHDL is a hardware schematic language.
(Source: Wikimedia Commons)
### Postulates
In binary algebra, if $x,y,z\in\mathbb B$ such that $\mathbb B=\{0, 1\}$:
The **identity element** for **AND** $1$ is such that any $x\cdot 1 = x$.
The **identity element** for **OR** $0$ is such that any $x + 0 = x$.
In this space, it can be deduced that $x+x'=1$ and $x\cdot x'=0$.
**De Morgan's laws** are much easier to express in boolean algebra, and denote distributing a negation by flipping the operator:
$$
(x\cdot y)'=x'+y' \\
(x+y)=x'\cdot y'
$$
Please see [ECE 108: Discrete Math 1#Operator laws](/1b/ece108/#operator-laws) for more information.
AND and OR are commutative.
- $x\cdot y=y\cdot x$
- $x+y=y+x$
AND and OR are associative.
- $x\cdot(y\cdot z)=(x\cdot y)\cdot z)$
- ...
AND and OR are distributive with each other.
- $x\cdot (y+z)=x\cdot y+z\cdot z$
A term that depends on another term ORed together can be "absorbed".
- $x+x\cdot y=x$
- $x\cdot(x+y)=x$
If a term being true also results in other ORed terms being true, it is redundant and can be eliminated via consensus.
- $x\cdot y+y\cdot z+x'\cdot z=x\cdot y+x'\cdot z$
- if y and z are true, at least one of the other two terms must be true
- $(x+y)\cdot (y+z)\cdot(x'+z)=(x+y)\cdot (x'+z)$
The **synthesis** of an algebraic formula represents its implementation via logic gates. In this course, its total cost is the sum of all inputs to all gates and the number of gates, *excluding* initial inputs of "true" or an initial negation.
In order to deduce an algebraic expression from a truth table, **OR** all of the rows in which the function returns true and simplify.
??? example
Prove that $(x+y)\cdot(x+y')=x$:
\begin{align*}
\tag{distributive property}(x+y)\cdot(x+y')&=xx+xy'+yx+yy' \\
\tag{$yy'$ = 0, $xx=x$}&=x + xy' + yx \\
\tag{distributive, commutative properties}&= x(1+y'+y) \\
\tag{1 + ... = 1}&= x(1) \\
&=x
\end{align*}
Prove that $xy+yz+x'z=xy+x'z$:
\begin{align*}
\tag{$x+x'=1$}xy+yz+x'z&=xy+yz(x+x')+x'z \\
\tag{distributive property}&=xy+xyz+x'yz+x'z \\
\tag{distributive property}&=x(y+yz) + x'(yz+z) \\
\tag{distributive property}&=xy(1+z) + x'z(y+1) \\
\tag{$1+k=1$}&=xy(1) + x'z(1) \\
\tag{$1\cdot k=k$}&= xy+x'z
\end{align*}
### Minterms and maxterms
The **minterm** $m$ is a **product** term where all variables in the function appear once. There are $2^n$ minterms for each function, where $n$ is the number of input variables.
To determine the relevant function, the subscript can be converted to binary and each function variable set such that:
- if the digit is $1$, the complement is used, and
- if the digit is $0$, the original is used.
$$m_j=x_1+x_2+\dots x_n$$
!!! example
For a function that accepts three variables:
- there are eight minterms, from $m_0$ to $m_7$.
- the sixth minterm $m_6=xyz'$ because $6=0b110$.
For a sample function defined by the following minterms:
$$
\begin{align*}
f(x_1,x_2,x_3)&=\sum m(1,2,5) \\
&=m_1+m_2+m_5 \\
&=x_1x_2x_3' + x_1x_2'x_3 + x_1'x_2x_3'
\end{align*}
$$
The **maxterm** $M$ is a **sum** term where all variables in the function appear once. It is more or less the same as a minterm, except the condition for each variable is **reversed** (i.e., $0$ indicates the complement).
$$M_j=x_1+x_2+\dots +x_n$$
!!! example
For a sample function defined by the following maxterms:
\begin{align*}
f(x_1,x_2,x_3,x_4)&=\prod M(1,2,8,12) \\
&=M_1M_2M_8M_{12} \\
\end{align*}
??? example
Prove that $\sum m(1,2,3,4,5,6,7)=x_1+x_2+x_3$: **(some shortcuts taken for visual clarity)**
\begin{align*}
\sum m(1,2,3,4,5,6,7) &=001+011+111+010+110+100+000 \\
\tag{SIMD distribution}&=001+010+100 \\
&=x_1+x_2+x_3
\end{align*}
A **canonical sum of products (SOP)** is a function expressed as a sum of minterms.
$$f(x_1,x_2,\dots)=\sum m(a,b, \dots)$$
A **canonical product of sums (POS)** is a function expressed as a product of maxterms.
$$f(x_1,x_2,\dots)=\prod M(a,b,\dots)$$
## VHDL
VHDL is a hardware schematic language.
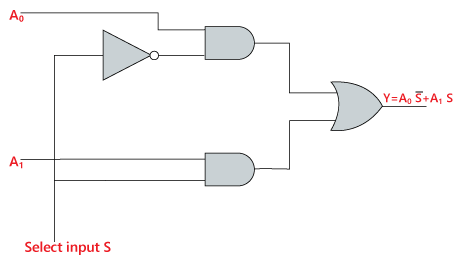 For example, the basic 2-to-1 multiplexer expressed above can be programmed as:
```vhdl
entity two_one_mux is
port (a0, s, a1 : in bit;
f : out bit);
end two_one_mux
architecture LogicFunc of two_one_mux is
begin
y <= (a0 AND s) OR (NOT s AND a1);
end LogicFunc;
```
In this case, the inputs are `a0, s, a1` that lead to an output `y`. All input/output is of type `bit` (a boolean).
The **architecture** defines how inputs translate to outputs via functions. These all run **concurrently**.
For example, the basic 2-to-1 multiplexer expressed above can be programmed as:
```vhdl
entity two_one_mux is
port (a0, s, a1 : in bit;
f : out bit);
end two_one_mux
architecture LogicFunc of two_one_mux is
begin
y <= (a0 AND s) OR (NOT s AND a1);
end LogicFunc;
```
In this case, the inputs are `a0, s, a1` that lead to an output `y`. All input/output is of type `bit` (a boolean).
The **architecture** defines how inputs translate to outputs via functions. These all run **concurrently**.
 For example, the basic 2-to-1 multiplexer expressed above can be programmed as:
```vhdl
entity two_one_mux is
port (a0, s, a1 : in bit;
f : out bit);
end two_one_mux
architecture LogicFunc of two_one_mux is
begin
y <= (a0 AND s) OR (NOT s AND a1);
end LogicFunc;
```
In this case, the inputs are `a0, s, a1` that lead to an output `y`. All input/output is of type `bit` (a boolean).
The **architecture** defines how inputs translate to outputs via functions. These all run **concurrently**.
For example, the basic 2-to-1 multiplexer expressed above can be programmed as:
```vhdl
entity two_one_mux is
port (a0, s, a1 : in bit;
f : out bit);
end two_one_mux
architecture LogicFunc of two_one_mux is
begin
y <= (a0 AND s) OR (NOT s AND a1);
end LogicFunc;
```
In this case, the inputs are `a0, s, a1` that lead to an output `y`. All input/output is of type `bit` (a boolean).
The **architecture** defines how inputs translate to outputs via functions. These all run **concurrently**.