# MATH 117: Calculus 1
## Functions
A **function** is a rule where each input has exactly one output, which can be determined by the **vertical line test**.
!!! definition
- The **domain** is the set of allowable independent values.
- The **range** is the set of allowable dependent values.
Functions can be **composed** to apply the result of one function to another.
$$
(f\circ g)(x) = f(g(x))
$$
!!! warning
Composition is not commutative: $f\circ g \neq g\circ f$.
## Inverse functions
The inverse of a function swaps the domain and range of the original function: $f^{-1}(x)$ is the inverse of $f(x)$.. It can be determined by solving for the other variable:
$$
\begin{align*}
y&=mx+b \\
y-b&=mx \\
x&=\frac{y-b}{m}
\end{align*}
$$
Because the domain and range are simply swapped, the inverse function is just the original function reflected across the line $y=x$.
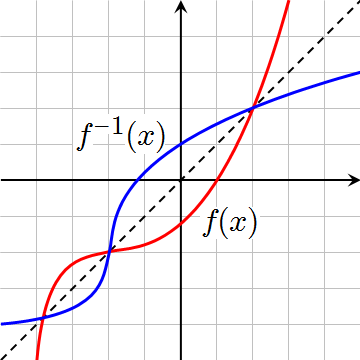 (Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example
(Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example
 (Source: Wikimedia Commons, public domain)
By restricting the domain to $[0,\inf]$, the **multivalued inverse function** $y=\pm\sqrt{x}$ is reduced to just the partial inverse $y=\sqrt{x}$.
## Symmetry
An **even function** satisfies the property that $f(x)=f(-x)$, indicating that it is unchanged by a reflection across the y-axis.
An **odd function** satisfies the property that $-f(x)=f(-x)$, indicating that it is unchanged by a 180° rotation about the origin.
The following properties are always true for even and odd functions:
- even × even = even
- odd × odd = even
- even × odd = odd
Functions that are symmetric (that is, both $f(x)$ and $f(-x)$ exist) can be split into an even and odd component. Where $g(x)$ is the even component and $h(x)$ is the odd component:
$$
\begin{align*}
f(x) &= g(x) + h(x) \\
g(x) &= \frac{1}{2}(f(x) + f(-x)) \\
h(x) &= \frac{1}{2}(f(x) - f(-x))
\end{align*}
$$
!!! note
The hyperbolic sine and cosine are the even and odd components of $f(x)=e^x$.
$$
\cosh x = \frac{1}{2}(e^x + e^{-x}) \\
\sinh x = \frac{1}{2}(e^x - e^{-x})
$$
## Piecewise functions
A piecewise function is one that changes formulae at certain intervals. To solve piecewise functions, each of one's intervals should be considered.
### Absolute value function
$$
\begin{align*}
|x| = \begin{cases}
x &\text{ if } x\geq 0 \\
-x &\text{ if } x < 0
\end{cases}
\end{align*}
$$
### Signum function
The signum function returns the sign of its argument.
$$
\begin{align*}
\text{sgn}(x)=\begin{cases}
-1 &\text{ if } x < 0 \\
0 &\text{ if } x = 0 \\
1 &\text{ if } x > 0
\end{cases}
\end{align*}
$$
### Ramp function
The ramp function makes a ramp through the origin that suddenly flatlines at 0. Where $c$ is a constant:
$$
\begin{align*}
r(t)=\begin{cases}
0 &\text{ if } x \leq 0 \\
ct &\text{ if } x > 0
\end{cases}
\end{align*}
$$
(Source: Wikimedia Commons, public domain)
By restricting the domain to $[0,\inf]$, the **multivalued inverse function** $y=\pm\sqrt{x}$ is reduced to just the partial inverse $y=\sqrt{x}$.
## Symmetry
An **even function** satisfies the property that $f(x)=f(-x)$, indicating that it is unchanged by a reflection across the y-axis.
An **odd function** satisfies the property that $-f(x)=f(-x)$, indicating that it is unchanged by a 180° rotation about the origin.
The following properties are always true for even and odd functions:
- even × even = even
- odd × odd = even
- even × odd = odd
Functions that are symmetric (that is, both $f(x)$ and $f(-x)$ exist) can be split into an even and odd component. Where $g(x)$ is the even component and $h(x)$ is the odd component:
$$
\begin{align*}
f(x) &= g(x) + h(x) \\
g(x) &= \frac{1}{2}(f(x) + f(-x)) \\
h(x) &= \frac{1}{2}(f(x) - f(-x))
\end{align*}
$$
!!! note
The hyperbolic sine and cosine are the even and odd components of $f(x)=e^x$.
$$
\cosh x = \frac{1}{2}(e^x + e^{-x}) \\
\sinh x = \frac{1}{2}(e^x - e^{-x})
$$
## Piecewise functions
A piecewise function is one that changes formulae at certain intervals. To solve piecewise functions, each of one's intervals should be considered.
### Absolute value function
$$
\begin{align*}
|x| = \begin{cases}
x &\text{ if } x\geq 0 \\
-x &\text{ if } x < 0
\end{cases}
\end{align*}
$$
### Signum function
The signum function returns the sign of its argument.
$$
\begin{align*}
\text{sgn}(x)=\begin{cases}
-1 &\text{ if } x < 0 \\
0 &\text{ if } x = 0 \\
1 &\text{ if } x > 0
\end{cases}
\end{align*}
$$
### Ramp function
The ramp function makes a ramp through the origin that suddenly flatlines at 0. Where $c$ is a constant:
$$
\begin{align*}
r(t)=\begin{cases}
0 &\text{ if } x \leq 0 \\
ct &\text{ if } x > 0
\end{cases}
\end{align*}
$$
 (Source: Wikimedia Commons, public domain)
### Floor and ceiling functions
The floor function rounds down.
$$\lfloor x\rfloor$$
The ceiling function rounds up.
$$\lceil x \rceil$$
### Fractional part function
In a nutshell, the fractional part function:
- returns the part **after the decimal point** if the number is positive
- returns 1 - **the part after the decimal point** if the number is negative
$$\text{FRACPT}(x) = x-\lfloor x\rfloor$$
Because this function is periodic, it can be used to limit angles to the $[0, 2\pi)$ range with:
$$f(\theta) = 2\pi\cdot\text{FRACPT}\biggr(\frac{\theta}{2\pi}\biggr)$$
### Heaviside function
The Heaviside function effectively returns a boolean whether the number is greater than 0.
$$
\begin{align*}
H(x) = \begin{cases}
0 &\text{ if } t < 0 \\
1 &\text{ if } t \geq 0
\end{cases}
\end{align*}
$$
This can be used to construct other piecewise functions by enabling them with $H(x-a)$ as a factor, where $a$ is the interval.
In a nutshell:
- $1-H(t-a)$ lets you "turn a function off" at at $t=a$
- $H(t-a)$ lets you "turn a function on at $t=a$
- $H(t-a) - H(t-b)$ leaves a function on in the interval $(a, b)$
!!! example
TODO: example for converting piecewise to heaviside via collecting heavisides
and vice versa
## Periodicity
The function $f(t)$ is periodic only if there is a repeating pattern, i.e. such that for every $x$, there is an $f(x) = f(x + nT)$, where $T$ is the period and $n$ is any integer.
### Circular motion
Please see [SL Physics 1#6.1 - Circular motion](/g11/sph3u7/#61-circular-motion) and its subcategory "Angular thingies" for more information.
## Partial function decomposition (PFD)
In order to PFD:
1. Factor the denominator into *irreducibly* quadratic or linear terms.
2. For each factor, create a term. Where capital letters below are constants:
- A linear factor $Bx+C$ has a term $\frac{A}{Bx+C}$.
- An *irreducibly* quadratic factor $Dx^2+Ex+G$ has a term $\frac{Hx+J}{Dx^2+Ex+G}$.
- Duplicate factors have terms with denominators with that factor to the power of 1 up to the number of times the factor is present in the original.
4. Set the two equal to each other such that the denominators can be factored out.
5. Create systems of equations to solve for each constant.
!!! example
To decompose $\frac{x}{(x+1)(x^2+x+1)}$:
$$
\begin{align*}
\frac{x}{(x+1)(x^2+x+1)} &= \frac{A}{x+1} + \frac{Bx+C}{x^2+x+1} \\
&= \frac{A(x^2+x+1) + (Bx+C)(x+1)}{(x+1)(x^2+x+1)} \\
x &= A(x^2+x+1) + (Bx+C)(x+1) \\
0x^2 + x + 0 &= (Ax^2 + Bx^2) + (Ax + Bx + Cx) + (A + C) \\
\\
&\begin{cases}
0 = A + B \\
1 = A + B + C \\
0 = A + C
\end{cases}
\\
A &= -1 \\
B &= 1 \\
C &= 1 \\
\\
∴ \frac{x}{(x+1)(x^2+x+1)} &= -\frac{1}{x+1} + \frac{x + 1}{x^2 + x + 1}
\end{align*}
$$
## Trigonometry
1 radian represents the angle when the length of the arc of a circle is equal to the radius. Where $s$ is the arc length:
$$\theta=\frac{s}{r}$$
The following table indicates the special angles that should be memorised:
| Angle (rad) | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ |
| --- | --- | --- | --- | --- | --- | --- |
| cos | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | 0 | -1 |
| sin | 0 | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 | 0 |
| tan | 0 | $\frac{\sqrt{3}}{3}$ | 1 | $\sqrt{3}$ | not allowed | 0 |
### Identities
The Pythagorean identity is the one behind right angle triangles:
$$\cos^2\theta+\sin^2\theta = 1$$
Cosine and sine can be converted between by an angle shift:
$$
\cos\biggr(\theta-\frac{\pi}{2}\biggr) = \sin\theta \\
\sin\biggr(\theta-\frac{\pi}{2}\biggr) = \cos\theta
$$
The **angle sum identities** allow expanding out angles:
$$
\cos(a+b)=\cos a\cos b - \sin a\sin b \\
\sin(a+b)=\sin a\cos b + \cos a\sin b
$$
Subtracting angles is equal to the conjugates of the angle sum identities.
The **double angle identities** simplify the angle sum identity for a specific case.
$$
\sin2\theta = 2\sin\theta\cos\theta \\
$$
The **half angle formulas** are just random shit.
$$
1+\tan^2\theta = \sec^2\theta \\
\cos^2\theta = \frac{1}{2}(1+\cos2\theta) \\
\sin^2\theta = \frac{1}{2}(1-\cos2\theta)
$$
(Source: Wikimedia Commons, public domain)
### Floor and ceiling functions
The floor function rounds down.
$$\lfloor x\rfloor$$
The ceiling function rounds up.
$$\lceil x \rceil$$
### Fractional part function
In a nutshell, the fractional part function:
- returns the part **after the decimal point** if the number is positive
- returns 1 - **the part after the decimal point** if the number is negative
$$\text{FRACPT}(x) = x-\lfloor x\rfloor$$
Because this function is periodic, it can be used to limit angles to the $[0, 2\pi)$ range with:
$$f(\theta) = 2\pi\cdot\text{FRACPT}\biggr(\frac{\theta}{2\pi}\biggr)$$
### Heaviside function
The Heaviside function effectively returns a boolean whether the number is greater than 0.
$$
\begin{align*}
H(x) = \begin{cases}
0 &\text{ if } t < 0 \\
1 &\text{ if } t \geq 0
\end{cases}
\end{align*}
$$
This can be used to construct other piecewise functions by enabling them with $H(x-a)$ as a factor, where $a$ is the interval.
In a nutshell:
- $1-H(t-a)$ lets you "turn a function off" at at $t=a$
- $H(t-a)$ lets you "turn a function on at $t=a$
- $H(t-a) - H(t-b)$ leaves a function on in the interval $(a, b)$
!!! example
TODO: example for converting piecewise to heaviside via collecting heavisides
and vice versa
## Periodicity
The function $f(t)$ is periodic only if there is a repeating pattern, i.e. such that for every $x$, there is an $f(x) = f(x + nT)$, where $T$ is the period and $n$ is any integer.
### Circular motion
Please see [SL Physics 1#6.1 - Circular motion](/g11/sph3u7/#61-circular-motion) and its subcategory "Angular thingies" for more information.
## Partial function decomposition (PFD)
In order to PFD:
1. Factor the denominator into *irreducibly* quadratic or linear terms.
2. For each factor, create a term. Where capital letters below are constants:
- A linear factor $Bx+C$ has a term $\frac{A}{Bx+C}$.
- An *irreducibly* quadratic factor $Dx^2+Ex+G$ has a term $\frac{Hx+J}{Dx^2+Ex+G}$.
- Duplicate factors have terms with denominators with that factor to the power of 1 up to the number of times the factor is present in the original.
4. Set the two equal to each other such that the denominators can be factored out.
5. Create systems of equations to solve for each constant.
!!! example
To decompose $\frac{x}{(x+1)(x^2+x+1)}$:
$$
\begin{align*}
\frac{x}{(x+1)(x^2+x+1)} &= \frac{A}{x+1} + \frac{Bx+C}{x^2+x+1} \\
&= \frac{A(x^2+x+1) + (Bx+C)(x+1)}{(x+1)(x^2+x+1)} \\
x &= A(x^2+x+1) + (Bx+C)(x+1) \\
0x^2 + x + 0 &= (Ax^2 + Bx^2) + (Ax + Bx + Cx) + (A + C) \\
\\
&\begin{cases}
0 = A + B \\
1 = A + B + C \\
0 = A + C
\end{cases}
\\
A &= -1 \\
B &= 1 \\
C &= 1 \\
\\
∴ \frac{x}{(x+1)(x^2+x+1)} &= -\frac{1}{x+1} + \frac{x + 1}{x^2 + x + 1}
\end{align*}
$$
## Trigonometry
1 radian represents the angle when the length of the arc of a circle is equal to the radius. Where $s$ is the arc length:
$$\theta=\frac{s}{r}$$
The following table indicates the special angles that should be memorised:
| Angle (rad) | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ | $\pi$ |
| --- | --- | --- | --- | --- | --- | --- |
| cos | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | 0 | -1 |
| sin | 0 | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 | 0 |
| tan | 0 | $\frac{\sqrt{3}}{3}$ | 1 | $\sqrt{3}$ | not allowed | 0 |
### Identities
The Pythagorean identity is the one behind right angle triangles:
$$\cos^2\theta+\sin^2\theta = 1$$
Cosine and sine can be converted between by an angle shift:
$$
\cos\biggr(\theta-\frac{\pi}{2}\biggr) = \sin\theta \\
\sin\biggr(\theta-\frac{\pi}{2}\biggr) = \cos\theta
$$
The **angle sum identities** allow expanding out angles:
$$
\cos(a+b)=\cos a\cos b - \sin a\sin b \\
\sin(a+b)=\sin a\cos b + \cos a\sin b
$$
Subtracting angles is equal to the conjugates of the angle sum identities.
The **double angle identities** simplify the angle sum identity for a specific case.
$$
\sin2\theta = 2\sin\theta\cos\theta \\
$$
The **half angle formulas** are just random shit.
$$
1+\tan^2\theta = \sec^2\theta \\
\cos^2\theta = \frac{1}{2}(1+\cos2\theta) \\
\sin^2\theta = \frac{1}{2}(1-\cos2\theta)
$$
 (Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example
(Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example