diff --git a/Grade 9/Math.md b/Grade 9/Math.md
new file mode 100644
index 0000000..651c255
--- /dev/null
+++ b/Grade 9/Math.md
@@ -0,0 +1,585 @@
+# Math Study Sheet!!!!
+
+# Essential Skills (1)
+> ## Simple Arithmetics
+>> ### Addition / Subtraction
+>>> | Expression | Equivalent|
+>>> |:----------:|:---------:|
+>>> | a + b | a + b |
+>>> | (-a) + b | b - a |
+>>> | a + (-b) | a - b |
+>>> | (-a) + (-b) | -(a + b) |
+>>> | a - b | a - b|
+>>> | a - (-b) | a + b |
+>>> | (-a) -(-b) | (-a) + b|
+
+>> ### Multiplication / Division
+>>> | Signs | Outcome |
+>>> |:-----:|:-------:|
+>>> | a * b | Positive |
+>>> | (-a) * b | Negative |
+>>> | a * (-b) | Negative |
+>>> | (-a) * (-b) | Positive |
+
+>> ### BEDMAS / PEMDAS
+>>> Follow ```BEDMAS``` for order of operations if there are more than one operation
+
+>>> | Letter | Meaning |
+>>> |:------:|:-------:|
+>>> | B / P | Bracket / Parentheses |
+>>> | E | Exponent |
+>>> | D | Divison |
+>>> | M | Multiplication |
+>>> | A | Addition |
+>>> | S | Subtraction |
+
+>>>  +
+> ## Interval Notation
+>> A notation that represents an interval as a pair of numbers.
+>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
+>> ```|``` means ```such that```
+>> ```E``` or ∈ means ```element of```
+>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
+>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
+>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≥ ∞, x ∈ Z})
+>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
+
+>> | Symbol | Meaning |
+>> |:------:|:-------:|
+>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
+>> | [a, b] | Inclusive |
+>> | a ∪ b | Union (or) |
+>> | a ∩ b | Intersection (and) |
+
+> ## Pythgorean Theorem
+>> let a be the adjecant and b be the opposite, and c be the hypotenuse.
+>> a2 + b2 = c2
+
+>>
+
+> ## Interval Notation
+>> A notation that represents an interval as a pair of numbers.
+>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
+>> ```|``` means ```such that```
+>> ```E``` or ∈ means ```element of```
+>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
+>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
+>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≥ ∞, x ∈ Z})
+>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
+
+>> | Symbol | Meaning |
+>> |:------:|:-------:|
+>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
+>> | [a, b] | Inclusive |
+>> | a ∪ b | Union (or) |
+>> | a ∩ b | Intersection (and) |
+
+> ## Pythgorean Theorem
+>> let a be the adjecant and b be the opposite, and c be the hypotenuse.
+>> a2 + b2 = c2
+
+>>  +
+> ## Operations with Rationals
+>> Q = { a⁄b | a, b ∈ Z, b ≠ 0 }
+>> Any operations with rationals, there are 2 sets of rules
+>>> 1. ```Rules for operations with integers```
+>>> 2. ```Rules for operations with fractions```
+
+>> To Add / subtract rationals, find common denominator and then add / subtract numerator
+>> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
+>> To Divide rationals, multiply them by the reciprocal
+>> ### Example Simplify Fully:
+>>> = 3⁄4 ÷ 2⁄12 [Reduce to lowest terms]
+>>> = 3⁄4 ÷ 1⁄7 [Multiply by reciprocal]
+>>> = 3⁄4 × 7
+>>> = 21⁄4 [Leave as an improper fraction]
+
+>> ### Shortcut for multiplying fractions
+>>> cross divide to keep your numbers small
+>>> Example:
+>>> 2⁄4 × 4⁄6
+>>> 1⁄1 × 1⁄3
+>>> = 1⁄3
+
+>> ## Exponent Laws
+
+>>> | Rule | Description| Example |
+>>> |:----:|:----------:|:-------:|
+>>> |Product|am × an = an+m|23 × 22 = 25|
+>>> |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
+>>> |Power of a Power|(am)n = amn|(23)2 = 26|
+>>> |Power of a Quotient|(a⁄b)n = an⁄bn|(2⁄3)4 = 24⁄(34)|
+>>> |Zero as Exponents|a0 = 1|210 = 1|
+>>> |Negative Exponents|a-m = 1⁄am|1-10 = 1⁄(110) or 1⁄1|
+>>> |Rational Exponents|an/m = (m√a)n|165/4 = (4√16)5 = 25|
+
+>>> **Note:**
+>>> Standard --> Expanded Form
+>>> 64 = 6 × 6 × 6 × 6
+
+>> ## Scientific Notation
+>>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
+>>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
+>>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
+>>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
+>>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+
+>>>
+
+> ## Operations with Rationals
+>> Q = { a⁄b | a, b ∈ Z, b ≠ 0 }
+>> Any operations with rationals, there are 2 sets of rules
+>>> 1. ```Rules for operations with integers```
+>>> 2. ```Rules for operations with fractions```
+
+>> To Add / subtract rationals, find common denominator and then add / subtract numerator
+>> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
+>> To Divide rationals, multiply them by the reciprocal
+>> ### Example Simplify Fully:
+>>> = 3⁄4 ÷ 2⁄12 [Reduce to lowest terms]
+>>> = 3⁄4 ÷ 1⁄7 [Multiply by reciprocal]
+>>> = 3⁄4 × 7
+>>> = 21⁄4 [Leave as an improper fraction]
+
+>> ### Shortcut for multiplying fractions
+>>> cross divide to keep your numbers small
+>>> Example:
+>>> 2⁄4 × 4⁄6
+>>> 1⁄1 × 1⁄3
+>>> = 1⁄3
+
+>> ## Exponent Laws
+
+>>> | Rule | Description| Example |
+>>> |:----:|:----------:|:-------:|
+>>> |Product|am × an = an+m|23 × 22 = 25|
+>>> |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
+>>> |Power of a Power|(am)n = amn|(23)2 = 26|
+>>> |Power of a Quotient|(a⁄b)n = an⁄bn|(2⁄3)4 = 24⁄(34)|
+>>> |Zero as Exponents|a0 = 1|210 = 1|
+>>> |Negative Exponents|a-m = 1⁄am|1-10 = 1⁄(110) or 1⁄1|
+>>> |Rational Exponents|an/m = (m√a)n|165/4 = (4√16)5 = 25|
+
+>>> **Note:**
+>>> Standard --> Expanded Form
+>>> 64 = 6 × 6 × 6 × 6
+
+>> ## Scientific Notation
+>>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
+>>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
+>>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
+>>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
+>>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+
+>>>  +
+>> ## Rates, Ratio and Percent
+>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+>>> Examples: ```a:b, a:b:c, a/b, a to b ```
+
+>>> ```Rates```: A comparison of quantities expressed in different units.
+>>> Example: ```10km/hour```
+
+>>> ```Percent```: A fraction or ratio in which the denominator is 100
+>>> Examples: ```50%, 240/100```
+
+> ## Number Lines
+>> a line that goes from a point to another point, a way to visualize set notations and the like
+>>
+
+>> ## Rates, Ratio and Percent
+>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+>>> Examples: ```a:b, a:b:c, a/b, a to b ```
+
+>>> ```Rates```: A comparison of quantities expressed in different units.
+>>> Example: ```10km/hour```
+
+>>> ```Percent```: A fraction or ratio in which the denominator is 100
+>>> Examples: ```50%, 240/100```
+
+> ## Number Lines
+>> a line that goes from a point to another point, a way to visualize set notations and the like
+>>  +>> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+
+
+> ## Tips
+>> Watch out for the ```+/-``` signs
+>> Make sure to review your knowledge of the exponent laws
+>> For scientific notation, watch out for the decimal point
+>> Use shortcut when multiplying fractions
+
+
+# Polyomials (2)
+> ## Introduction to Polynomials
+>> A ```variable``` is a letter that represents one or more numbers
+>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
+>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+> ## Methods to solve a polynomial
+>> 1. ```Combine like terms```
+>> 2. ```Dividing polynomials```
+>> 3. ```Multiplying polynomials```
+
+> ## Simplifying Alegebraic Expressions
+>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+
+> ## Factoring
+>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+>> (e.g 5x + 10 = 5(x + 2) ).
+
+>> |Type of Polynomial|Definition|
+>> |:-----------------|:---------|
+>> |Monomial|Polynomial that only has one term|
+>> |Binomial|Polynomial that only has 2 terms|
+>> |Trinomial|polynomial that only has 3 terms|
+
+>> |Type|Example|
+>> |:--:|:-----:|
+>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
+>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+
+> ## Shortcuts
+
+>>
+>> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+
+
+> ## Tips
+>> Watch out for the ```+/-``` signs
+>> Make sure to review your knowledge of the exponent laws
+>> For scientific notation, watch out for the decimal point
+>> Use shortcut when multiplying fractions
+
+
+# Polyomials (2)
+> ## Introduction to Polynomials
+>> A ```variable``` is a letter that represents one or more numbers
+>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
+>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+> ## Methods to solve a polynomial
+>> 1. ```Combine like terms```
+>> 2. ```Dividing polynomials```
+>> 3. ```Multiplying polynomials```
+
+> ## Simplifying Alegebraic Expressions
+>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+
+> ## Factoring
+>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+>> (e.g 5x + 10 = 5(x + 2) ).
+
+>> |Type of Polynomial|Definition|
+>> |:-----------------|:---------|
+>> |Monomial|Polynomial that only has one term|
+>> |Binomial|Polynomial that only has 2 terms|
+>> |Trinomial|polynomial that only has 3 terms|
+
+>> |Type|Example|
+>> |:--:|:-----:|
+>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
+>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+
+> ## Shortcuts
+
+>>  +
+> ## Foil / Rainbow Method
+>>
+
+> ## Foil / Rainbow Method
+>> 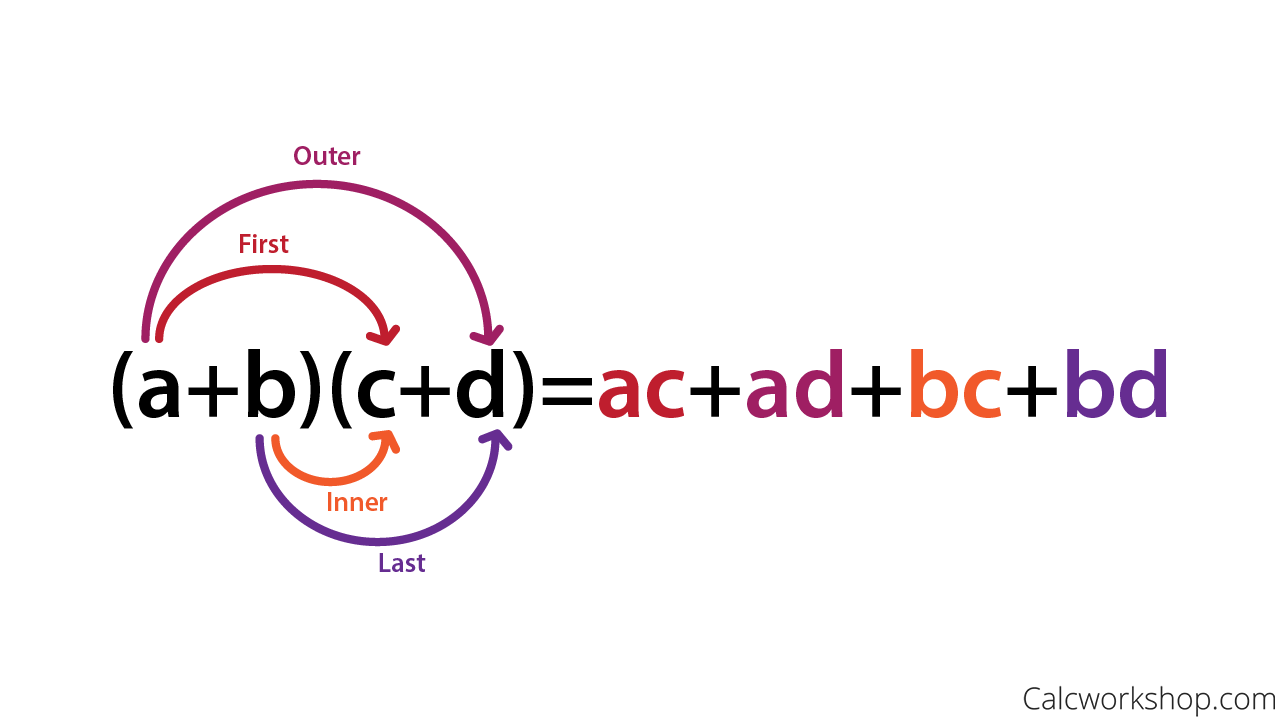 +
+> ## Definitions
+>> ```Term``` a variable that may have coefficient(s) or a constant
+>> ```Alebraic Expressions```: made up of one or more terms
+>> ```Like-terms```: same variables raised to the same exponent
+
+> ## Tips
+>> Be sure to factor fully
+>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+>> Remember your formulas
+>> Simplify first, combine like terms
+
+# Solving Equations and Inequailties (3)
+> ## Equations
+>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+>> To ```solve``` and equation is to find the variable that makes the statement true
+>> ### Methods to solve an equation
+>>> 1. Expand and simplify both sides
+>>> 2. Isolate using reverse order of operations
+>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+> ## Venn Diagrams
+
+>>
+
+> ## Definitions
+>> ```Term``` a variable that may have coefficient(s) or a constant
+>> ```Alebraic Expressions```: made up of one or more terms
+>> ```Like-terms```: same variables raised to the same exponent
+
+> ## Tips
+>> Be sure to factor fully
+>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+>> Remember your formulas
+>> Simplify first, combine like terms
+
+# Solving Equations and Inequailties (3)
+> ## Equations
+>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+>> To ```solve``` and equation is to find the variable that makes the statement true
+>> ### Methods to solve an equation
+>>> 1. Expand and simplify both sides
+>>> 2. Isolate using reverse order of operations
+>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+> ## Venn Diagrams
+
+>> 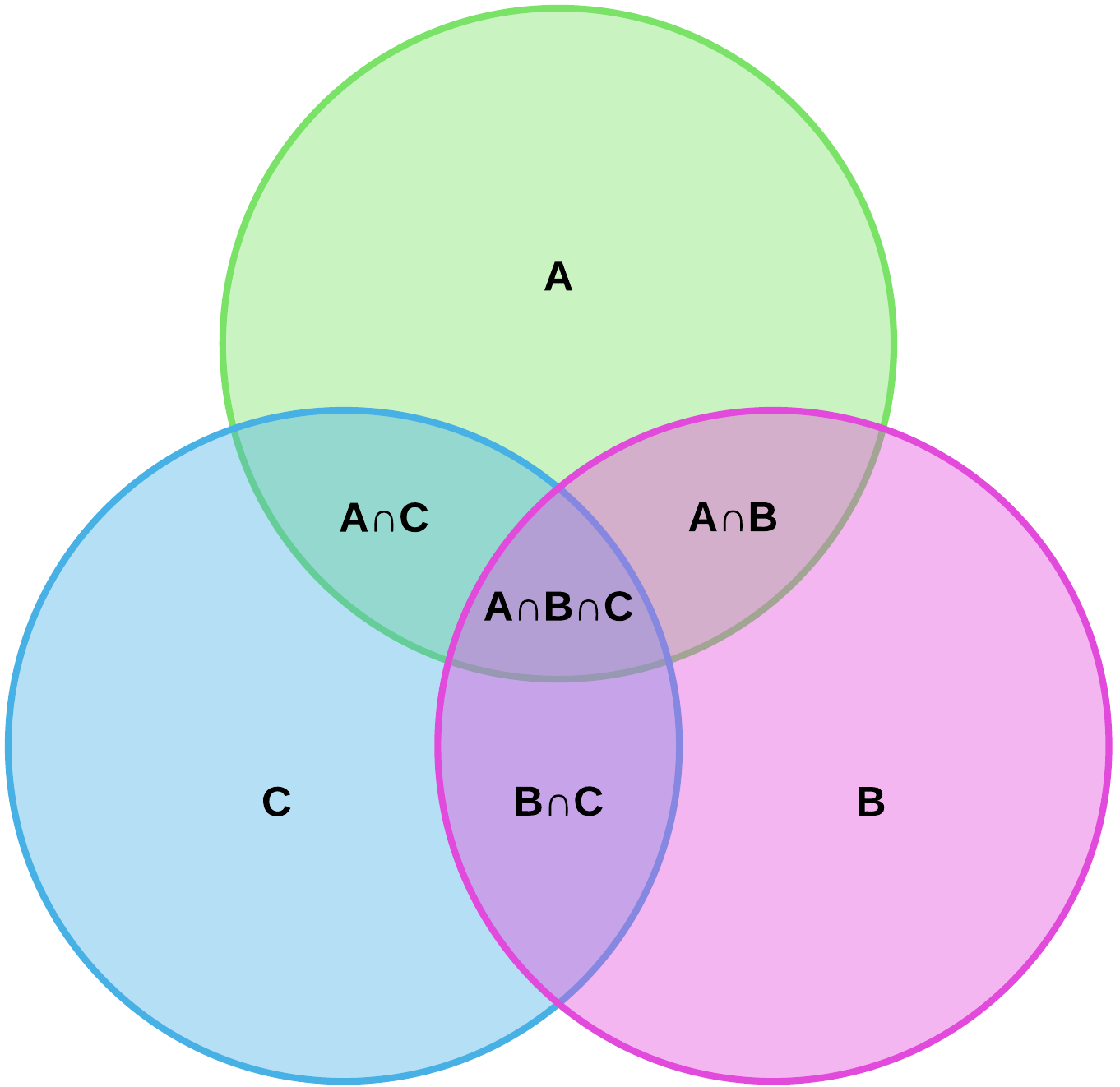 +
+>> ```Set```: a collection of elements, O (the circle)
+>> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
+>> ```Union```: ∪
+>> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
+>> ```Intersection```: ∩
+>> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
+>> ```Set Notation```:
+>> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
+>> ```Absolute Value```
+>>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>>> equations will have the absolute bracket be positive while the other negative.
+>>> Absolute values are written in the form ```| x |```
+>>> where
+>>> if x > 0, | x | = x
+>>> if x == 0, | x | = 0
+>>> if x < 0, | x | = -x
+
+> ## Quadractic Equations
+>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+>> Solve quadratic equation by:
+>> 1. Isolation
+>> a(x+b)2 + k = 0
+>> 2. Factor using zero-product property
+>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+>> (x-a)(x-b)=0
+>> x = a, b
+
+>>
+
+>> ```Set```: a collection of elements, O (the circle)
+>> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
+>> ```Union```: ∪
+>> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
+>> ```Intersection```: ∩
+>> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
+>> ```Set Notation```:
+>> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
+>> ```Absolute Value```
+>>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>>> equations will have the absolute bracket be positive while the other negative.
+>>> Absolute values are written in the form ```| x |```
+>>> where
+>>> if x > 0, | x | = x
+>>> if x == 0, | x | = 0
+>>> if x < 0, | x | = -x
+
+> ## Quadractic Equations
+>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+>> Solve quadratic equation by:
+>> 1. Isolation
+>> a(x+b)2 + k = 0
+>> 2. Factor using zero-product property
+>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+>> (x-a)(x-b)=0
+>> x = a, b
+
+>>  +
+>> Note:
+>> √x2 = ± x (There are 2 possible solutions)
+>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+>> ## Discriminant
+>>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+>>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
+>>> D = b2 - 4ac
+>>> D > 0 ```(2 distinct real solutions)```
+>>> D = 0 ```(1 real solution)```
+>>> D < 0 ```(no real solutions)```
+
+>>>
+
+>> Note:
+>> √x2 = ± x (There are 2 possible solutions)
+>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+>> ## Discriminant
+>>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+>>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
+>>> D = b2 - 4ac
+>>> D > 0 ```(2 distinct real solutions)```
+>>> D = 0 ```(1 real solution)```
+>>> D < 0 ```(no real solutions)```
+
+>>>  +
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>
+
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>  +
+> There are 3 possible cases
+> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
+
+> ## Tips
+>> ```Absolute Values``` can have 2 solutions
+>> ```Quadratics``` can also have 2 solutions
+>> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
+
+
+
+# Measurement and Geometry (4)
+> ## Angle Theorems
+> 1. ```Transversal Parallel Line Theorems``` (TPT)
+> a. Alternate Angles are Equal ```(Z-Pattern)```
+> b. Corresponding Angles Equal ```(F-Pattern)```
+> c. Interior Angles add up to 180 ```(C-Pattern)```
+
+>
+
+> There are 3 possible cases
+> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
+
+> ## Tips
+>> ```Absolute Values``` can have 2 solutions
+>> ```Quadratics``` can also have 2 solutions
+>> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
+
+
+
+# Measurement and Geometry (4)
+> ## Angle Theorems
+> 1. ```Transversal Parallel Line Theorems``` (TPT)
+> a. Alternate Angles are Equal ```(Z-Pattern)```
+> b. Corresponding Angles Equal ```(F-Pattern)```
+> c. Interior Angles add up to 180 ```(C-Pattern)```
+
+> 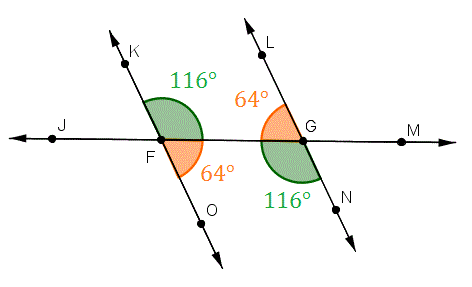 +
+> 2. ```Supplementary Angle Triangle``` (SAT)
+> - When two angles add up to 180 degrees
+
+>
+
+> 2. ```Supplementary Angle Triangle``` (SAT)
+> - When two angles add up to 180 degrees
+
+>  +
+> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
+> - Two lines intersect, two angles form opposite. They have equal measures
+
+>
+
+> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
+> - Two lines intersect, two angles form opposite. They have equal measures
+
+> 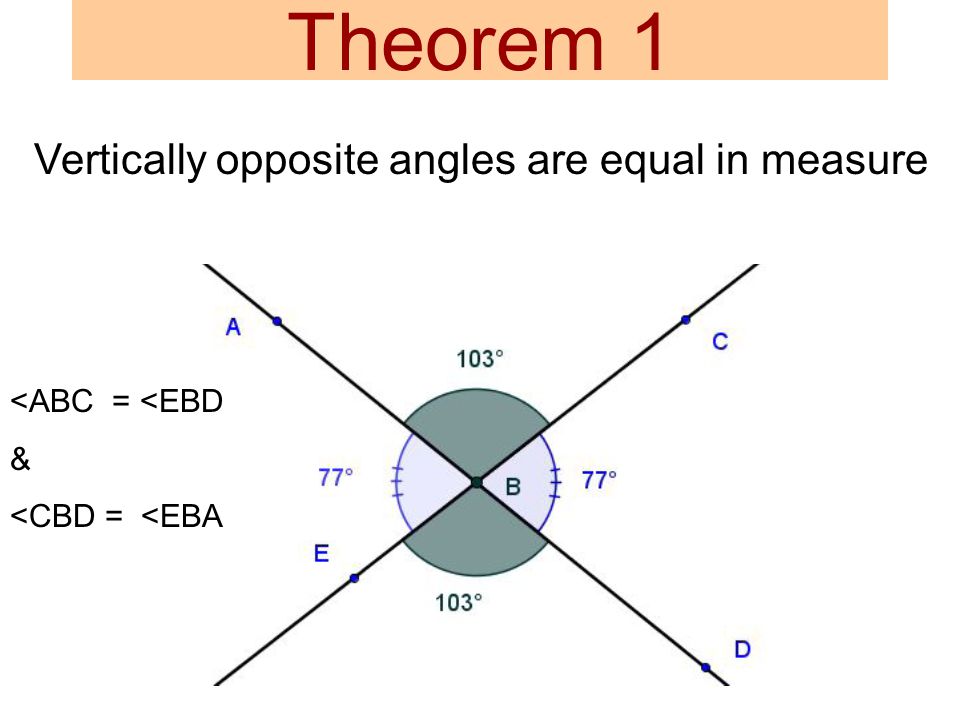 +
+> 4. ```Complementary Angle Theorem``` (CAT)
+> - The sum of two angles that add up to 90 degrees
+
+>
+
+> 4. ```Complementary Angle Theorem``` (CAT)
+> - The sum of two angles that add up to 90 degrees
+
+>  +
+> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+> - The sum of the three interior angles of any triangle is 180 degrees
+
+>
+
+> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+> - The sum of the three interior angles of any triangle is 180 degrees
+
+>  +
+> 6. ```Exterior Angle Theorem``` (EAT)
+> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+
+>
+
+> 6. ```Exterior Angle Theorem``` (EAT)
+> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+
+>  +
+> 7. ``` Isosceles Triangle Theorem``` (ITT)
+> - The base angles in any isosceles triangle are equal
+
+>
+
+> 7. ``` Isosceles Triangle Theorem``` (ITT)
+> - The base angles in any isosceles triangle are equal
+
+>  +
+> ## Properties of Quadrilaterals
+>> Determine the shape using the properties of it
+
+>> |Figure|Properties|
+>> |:-----|:---------|
+>> |Scalene Triangle|no sides equal|Length of line segment|
+>> |Isosceles Triangle| two sides equal|Length of line segment|
+>> |Equilateral Triangle|All sides equal|Length of line segment|
+>> |Right Angle Triangle|Two sides are perpendicular to each other|
+>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+>> |Kite|The diagonals are perpendicular|
+
+> ## 2D Geometry Equations
+>> |Shape|Formula|Picture|
+>> |:----|:------|:------|
+>> |Rectangle|```Area```: lw
+
+> ## Properties of Quadrilaterals
+>> Determine the shape using the properties of it
+
+>> |Figure|Properties|
+>> |:-----|:---------|
+>> |Scalene Triangle|no sides equal|Length of line segment|
+>> |Isosceles Triangle| two sides equal|Length of line segment|
+>> |Equilateral Triangle|All sides equal|Length of line segment|
+>> |Right Angle Triangle|Two sides are perpendicular to each other|
+>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+>> |Kite|The diagonals are perpendicular|
+
+> ## 2D Geometry Equations
+>> |Shape|Formula|Picture|
+>> |:----|:------|:------|
+>> |Rectangle|```Area```: lw
```Perimeter```: 2(l+w)| |
+>> |Triangle|```Area```: bh/2
|
+>> |Triangle|```Area```: bh/2
```Perimeter```: a+b+c| |
+>> |Circle|```Area```: πr2
|
+>> |Circle|```Area```: πr2
```Circumference```: 2πr or πd| |
+>> |Trapezoid|```Area```: (a+b)h/2
|
+>> |Trapezoid|```Area```: (a+b)h/2
```Perimeter```: a+b+c+d| |
+
+> ## 3D Geometry Equations
+>> |3D Object|Formula|Picture|
+>> |:----|:------|:------|
+>> |Rectangular Prism|```Volume```: lwh
|
+
+> ## 3D Geometry Equations
+>> |3D Object|Formula|Picture|
+>> |:----|:------|:------|
+>> |Rectangular Prism|```Volume```: lwh
```SA```: 2(lw+lh+wh)| |
+>> |Square Based Pyramid|```Volume```: 1⁄3b2h
|
+>> |Square Based Pyramid|```Volume```: 1⁄3b2h
```SA```: 2bs+b2| |
+>> |Sphere|```Volume```: 4⁄3πr3
|
+>> |Sphere|```Volume```: 4⁄3πr3
```SA```: 4πr2| |
+>> |Cone|```Volume```: 1⁄3πr2h
|
+>> |Cone|```Volume```: 1⁄3πr2h
```SA```: πrs+πr2| |
+>> |Cylinder|```Volume```: πr2h
|
+>> |Cylinder|```Volume```: πr2h
```SA```: 2πr2+2πh| |
+>> |Triangular Prism|```Volume```: ah+bh+ch+bl
|
+>> |Triangular Prism|```Volume```: ah+bh+ch+bl
```SA```: 1⁄2blh| |
+
+
+> ## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
+>> ### 2D Objects
+
+>> |Shape|Maximum Area|Minimum Perimeter|
+>> |:----|:-----------|:----------------|
+>> |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
|
+
+
+> ## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
+>> ### 2D Objects
+
+>> |Shape|Maximum Area|Minimum Perimeter|
+>> |:----|:-----------|:----------------|
+>> |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
A = lw
Amax = (w)(w)
Amax = w2|A rectangle must be a square to minimaze the perimeter for a given area. The length is equal to the width.
P = 2(l+w)
Pmin = 2(w)(w)
Pmin = 2(2w)
Pmin = 4w|
+>> |3-sided rectangle|l = 2w
A = lw
Amax = 2w(w)
Amax = 2w2|l = 2w
P = l+w2
Pmin = 2w+2w
Pmin = 4w|
+
+
+>> ### 3D Objects
+
+>> |3D Object|Maximum Volumne|Minimum Surface Area|
+>> |:--------|:--------------|:-------------------|
+>> |Cylinder(closed-top)|The cylinder must be similar to a cube where h = 2r
V = πr2h
Vmax = πr2(2r)
Vmax = 2πr2|The cylinder must be similar to a cube where h = 2r
SA = 2πr2+2πrh
SAmin = 2πr2+2πr(2r)
SAmin = 2πr2+4πr2
SAmin = 6πr2|
+>> |Rectangular Prism(closed-top)|The prism must be a cube,
where l = w = h
V = lwh
Vmax = (w)(w)(w)
Vmax = w3|The prism must be a cube,
where l = w = h
SA = 2lh+2lw+2wh
SAmin = 2w2+2w2+2w2
SAmin = 6w2|
+>> |Cylinder(open-top)|h = r
V = πr2h
Vmax = πr2(r)
Vmax = πr3|h = r
SA = πr2+2πrh
SAmin = πr2+2πr(r)
SAmin = πr2+2πr2
SAmin = 3πr2|
+>> |Square-Based Rectangular Prism(open-top)|h = w/2
V = lwh
Vmax = (w)(w)(w⁄2)
Vmax = w3⁄2|h = w/2
SA = w2+4wh
SAmin = w2+4w(w⁄2)
SAmin = w2+2w2
SAmin = 3w2|
+
+> ## Labelling
+>> Given any polygons, labelling the vertices must always:
+>> 1. use ```CAPITAL LETTERS```
+>> 2. they have to be labeled in ```clockwise``` or ```counter-clockwise``` directions
+>> For a triangle, the side lengths are labeled in ```LOWERCASE LETTERS``` associated to the opposite side of the vertex
+
+>> 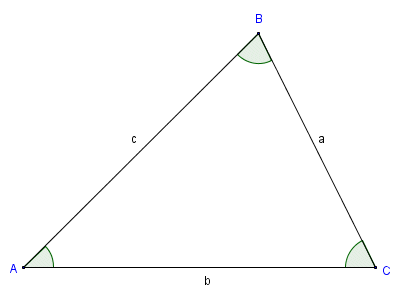 +
+> ## Median
+>> Each median divides the triangle into 2 smaller triangles of equal area
+>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
+>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
+
+>>
+
+> ## Median
+>> Each median divides the triangle into 2 smaller triangles of equal area
+>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
+>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
+
+>>  +
+> ## Terms:
+>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
+>>>
+
+> ## Terms:
+>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
+>>> 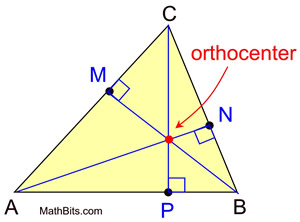 +>> ```Midpoint```: A point on a line where the length of either side of the point are equal
+>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+>> ```Centroid```: The intersection of the 3 medians of a triangle
+>>>
+>> ```Midpoint```: A point on a line where the length of either side of the point are equal
+>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+>> ```Centroid```: The intersection of the 3 medians of a triangle
+>>>  +
+> ## Proportionality theorem:
+>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+>>
+
+> ## Proportionality theorem:
+>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+>>  +
+> ## Tips
+>> Make sure to know your optimization formualas
+>> Read the word problems carefully, determine which formual to use
+>> Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
+>> To find ```missing area```, take what you have, subtract what you don't want
+>> Don't be afraid to draw lines to help you solve the problem
+
+
+# Analytical Geometry and Linear Relations (5)
+> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
+> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
+> ## Slope and Equation of Line
+>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```change in y / change in x```
+>> ```Slope Formula```: **m = y2-y1/x2-x1**
+>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
+>> ```Y-intercept Form```: **y = mx + b**
+>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
+>> The slope of a vertical lines is undefined
+>> The sloope of a horizontal line is 0
+>> Parallel lines have the ```same slope```
+>> Perpendicular slopes are negative reciprocals
+
+> ## Relations
+>> A relation can be described using
+>> 1. Table of Values (see below)
+>> 2. Equations (y = 3x + 5)
+>> 3. Graphs (Graphing the equation)
+>> 4. Words
+>> When digging into the earth, the temperature rises according to the
+>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
+>> degrees and **h** is the depth in meters.
+
+> ## Perpendicular Bisector
+>> To find the perpendicular bisector, you will need to fidn the slope and midpoint
+>> Formula: slope1 × slope2 = -1
+>> Notation: m⊥
+>>
+
+> ## Tips
+>> Make sure to know your optimization formualas
+>> Read the word problems carefully, determine which formual to use
+>> Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
+>> To find ```missing area```, take what you have, subtract what you don't want
+>> Don't be afraid to draw lines to help you solve the problem
+
+
+# Analytical Geometry and Linear Relations (5)
+> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
+> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
+> ## Slope and Equation of Line
+>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```change in y / change in x```
+>> ```Slope Formula```: **m = y2-y1/x2-x1**
+>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
+>> ```Y-intercept Form```: **y = mx + b**
+>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
+>> The slope of a vertical lines is undefined
+>> The sloope of a horizontal line is 0
+>> Parallel lines have the ```same slope```
+>> Perpendicular slopes are negative reciprocals
+
+> ## Relations
+>> A relation can be described using
+>> 1. Table of Values (see below)
+>> 2. Equations (y = 3x + 5)
+>> 3. Graphs (Graphing the equation)
+>> 4. Words
+>> When digging into the earth, the temperature rises according to the
+>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
+>> degrees and **h** is the depth in meters.
+
+> ## Perpendicular Bisector
+>> To find the perpendicular bisector, you will need to fidn the slope and midpoint
+>> Formula: slope1 × slope2 = -1
+>> Notation: m⊥
+>> 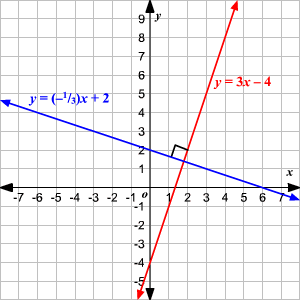 +
+
+> ## Definitions
+>> ```Parallel```: 2 lines with the same slope
+>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+>> ```Collinear Points```: points that line on the same straight line
+
+> ## Variables
+>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+> ## Statistics
+>> ```Interpolation```: Data **inside** the given data set range.
+>> ```Extrapolation```: Data **outside** the data set range.
+>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+>> and it represents the trend of a graph.
+>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+> ## Time - Distance Graph
+>> Time is the independent variable and distance is the dependent variable
+>> You can't go backwards on the x-axis, as you can't go back in time
+>> Plot the points accordingly
+>> Draw the lines accordingly
+>>
+
+
+> ## Definitions
+>> ```Parallel```: 2 lines with the same slope
+>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+>> ```Collinear Points```: points that line on the same straight line
+
+> ## Variables
+>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+> ## Statistics
+>> ```Interpolation```: Data **inside** the given data set range.
+>> ```Extrapolation```: Data **outside** the data set range.
+>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+>> and it represents the trend of a graph.
+>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+> ## Time - Distance Graph
+>> Time is the independent variable and distance is the dependent variable
+>> You can't go backwards on the x-axis, as you can't go back in time
+>> Plot the points accordingly
+>> Draw the lines accordingly
+>> 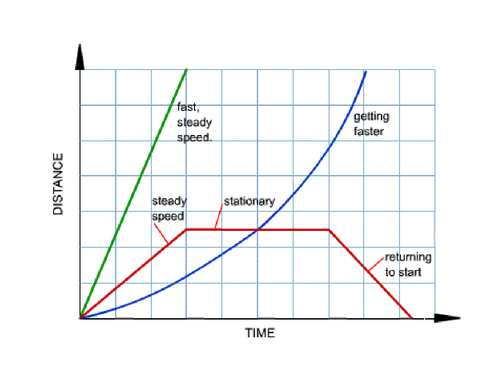 +
+> ## Scatterplot and Line of Best Fit
+>> A scatterplot graph is there to show the relation between two variables in a table of values.
+>> A line of best fit is a straight line that describes the relation between two variables.
+>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+>>
+
+> ## Scatterplot and Line of Best Fit
+>> A scatterplot graph is there to show the relation between two variables in a table of values.
+>> A line of best fit is a straight line that describes the relation between two variables.
+>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+>>  +
+> ## Table of values
+>> To find first differences or any points on the line, you can use a ```table of values```
+
+>>| y | x |First Difference|
+>>|:--|:--|:---------------|
+>>|-1|-2|1|
+>>|0|-1|1|
+>>|1|0|1|
+>>|2|1|1|
+>>|3|2|1|
+>>|4|3|1|
+
+> ## Tips
+>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+>> Draw your ```Line of Best Fit``` correctly
+>> Read the word problems carefully, and make sure you understand it when graphing things
+>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+>> Label your lines
+
+# System of Equations (6)
+
+> ## Linear System
+>> Two or more equation that you are working on all together at once on the same set of axes.
+>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+>> when **Profit = 0**. There is no gain or loss.
+
+>> ### Number of Solutions
+>>>
+
+> ## Table of values
+>> To find first differences or any points on the line, you can use a ```table of values```
+
+>>| y | x |First Difference|
+>>|:--|:--|:---------------|
+>>|-1|-2|1|
+>>|0|-1|1|
+>>|1|0|1|
+>>|2|1|1|
+>>|3|2|1|
+>>|4|3|1|
+
+> ## Tips
+>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+>> Draw your ```Line of Best Fit``` correctly
+>> Read the word problems carefully, and make sure you understand it when graphing things
+>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+>> Label your lines
+
+# System of Equations (6)
+
+> ## Linear System
+>> Two or more equation that you are working on all together at once on the same set of axes.
+>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+>> when **Profit = 0**. There is no gain or loss.
+
+>> ### Number of Solutions
+>>>  +
+> # Ways to solve Systems of Equations
+> 1. Subsitution
+> Here we eliminate a variable by subbing in another variable from another equation
+> We usually do this method if a variable is easily isolated
+> Example:
+> - ```
+> y = x + 10 (1)
+> x + y + 34 = 40 (2)
+> ```
+> We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
+> ```x + (x + 10) + 34 = 40```
+> ```2x + 44 = 40```
+> ```2x = -4```
+> ```x = -2```
+> Then solve for ```y```
+> ```y = -2 + 10```
+> ```y = -8```
+
+> 2. Elimination
+> Here we eliminate a variable by basically eliminate a variable from an equation
+> We usually use this method first when the variables are not easily isolated, then use subsitution to solve
+> Example:
+> - ```
+> 2x + 3y = 10 (1)
+> 4x + 3y = 14 (2)
+> ```
+> We can then use elimination
+> ```
+> 4x + 3y = 14
+> 2x + 3y = 10
+> ------------
+> 2x + 0 = 4
+> x = 2
+> ```
+> Then sub the value of ```x``` into an original equation and solve for ```y```
+> ```2(2) + 3y = 10```
+> ```3y = 6```
+> ```y = 2```
+
+> 3. Graphing
+> we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
+
+> ## Solving Systems of Linear Inequalities
+>> Find the intersection region as the ```solution```.
+>> ## If:
+
+>> | |Use ```Dash``` line|Use ```Solid line```|
+>> |:-|:------------------|:-------------------|
+>> |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
+>> |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
+
+>> ## If
+
+>> |x > a
+
+> # Ways to solve Systems of Equations
+> 1. Subsitution
+> Here we eliminate a variable by subbing in another variable from another equation
+> We usually do this method if a variable is easily isolated
+> Example:
+> - ```
+> y = x + 10 (1)
+> x + y + 34 = 40 (2)
+> ```
+> We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
+> ```x + (x + 10) + 34 = 40```
+> ```2x + 44 = 40```
+> ```2x = -4```
+> ```x = -2```
+> Then solve for ```y```
+> ```y = -2 + 10```
+> ```y = -8```
+
+> 2. Elimination
+> Here we eliminate a variable by basically eliminate a variable from an equation
+> We usually use this method first when the variables are not easily isolated, then use subsitution to solve
+> Example:
+> - ```
+> 2x + 3y = 10 (1)
+> 4x + 3y = 14 (2)
+> ```
+> We can then use elimination
+> ```
+> 4x + 3y = 14
+> 2x + 3y = 10
+> ------------
+> 2x + 0 = 4
+> x = 2
+> ```
+> Then sub the value of ```x``` into an original equation and solve for ```y```
+> ```2(2) + 3y = 10```
+> ```3y = 6```
+> ```y = 2```
+
+> 3. Graphing
+> we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
+
+> ## Solving Systems of Linear Inequalities
+>> Find the intersection region as the ```solution```.
+>> ## If:
+
+>> | |Use ```Dash``` line|Use ```Solid line```|
+>> |:-|:------------------|:-------------------|
+>> |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
+>> |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
+
+>> ## If
+
+>> |x > a
x ≥ a|
+>> |:------------------|
+>> shade the region on the **right**
+
+>> ## If
+
+>> |x < a
x ≤ a|
+>> |:------------------|
+>> shade the region on the **left**
+
+>> Step 1. change all inequalities to ```y-intercept form```
+>> Step 2. graph the line
+>> Step 3. shade the region where all the regions overlap
+
+>> 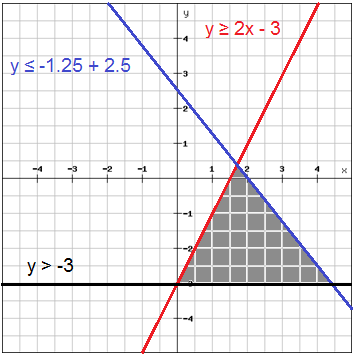 +
+> ## Tips
+>> Read the questions carefully and model the system of equations correctly
+>> Be sure to name your equations
+>> Label your lines
+
+# General Tips
+> Be sure to watch out for units, like ```cm``` or ```km```
+> Watch out for ```+/-```
+> Be sure to reverse the operation when moving things to the other side of the equation
+> Make sure to have a proper scale for graphs
+> Read question carefully and use the appropriate tools to solve
+> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+
+> ## Word Problems
+>> Read carefully
+>> model equations correctly
+>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+
+> ## Graph Problems
+>> Look up on tips in units (5) and (6)
+>> be sure to use a ruler when graphing
+
+> ## System of Equations
+>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+
+# Credits
+> Ryan Mark - He helped provide alot of information for me
+> Magicalsoup - ME!
+
+> ## Tips
+>> Read the questions carefully and model the system of equations correctly
+>> Be sure to name your equations
+>> Label your lines
+
+# General Tips
+> Be sure to watch out for units, like ```cm``` or ```km```
+> Watch out for ```+/-```
+> Be sure to reverse the operation when moving things to the other side of the equation
+> Make sure to have a proper scale for graphs
+> Read question carefully and use the appropriate tools to solve
+> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+
+> ## Word Problems
+>> Read carefully
+>> model equations correctly
+>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+
+> ## Graph Problems
+>> Look up on tips in units (5) and (6)
+>> be sure to use a ruler when graphing
+
+> ## System of Equations
+>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+
+# Credits
+> Ryan Mark - He helped provide alot of information for me
+> Magicalsoup - ME!
 +
+> ## Interval Notation
+>> A notation that represents an interval as a pair of numbers.
+>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
+>> ```|``` means ```such that```
+>> ```E``` or ∈ means ```element of```
+>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
+>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
+>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≥ ∞, x ∈ Z})
+>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
+
+>> | Symbol | Meaning |
+>> |:------:|:-------:|
+>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
+>> | [a, b] | Inclusive |
+>> | a ∪ b | Union (or) |
+>> | a ∩ b | Intersection (and) |
+
+> ## Pythgorean Theorem
+>> let a be the adjecant and b be the opposite, and c be the hypotenuse.
+>> a2 + b2 = c2
+
+>>
+
+> ## Interval Notation
+>> A notation that represents an interval as a pair of numbers.
+>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
+>> ```|``` means ```such that```
+>> ```E``` or ∈ means ```element of```
+>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
+>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
+>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≥ ∞, x ∈ Z})
+>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
+
+>> | Symbol | Meaning |
+>> |:------:|:-------:|
+>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
+>> | [a, b] | Inclusive |
+>> | a ∪ b | Union (or) |
+>> | a ∩ b | Intersection (and) |
+
+> ## Pythgorean Theorem
+>> let a be the adjecant and b be the opposite, and c be the hypotenuse.
+>> a2 + b2 = c2
+
+>>  +
+>> ## Rates, Ratio and Percent
+>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+>>> Examples: ```a:b, a:b:c, a/b, a to b ```
+
+>>> ```Rates```: A comparison of quantities expressed in different units.
+>>> Example: ```10km/hour```
+
+>>> ```Percent```: A fraction or ratio in which the denominator is 100
+>>> Examples: ```50%, 240/100```
+
+> ## Number Lines
+>> a line that goes from a point to another point, a way to visualize set notations and the like
+>>
+
+>> ## Rates, Ratio and Percent
+>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+>>> Examples: ```a:b, a:b:c, a/b, a to b ```
+
+>>> ```Rates```: A comparison of quantities expressed in different units.
+>>> Example: ```10km/hour```
+
+>>> ```Percent```: A fraction or ratio in which the denominator is 100
+>>> Examples: ```50%, 240/100```
+
+> ## Number Lines
+>> a line that goes from a point to another point, a way to visualize set notations and the like
+>>  +>> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+
+
+> ## Tips
+>> Watch out for the ```+/-``` signs
+>> Make sure to review your knowledge of the exponent laws
+>> For scientific notation, watch out for the decimal point
+>> Use shortcut when multiplying fractions
+
+
+# Polyomials (2)
+> ## Introduction to Polynomials
+>> A ```variable``` is a letter that represents one or more numbers
+>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
+>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+> ## Methods to solve a polynomial
+>> 1. ```Combine like terms```
+>> 2. ```Dividing polynomials```
+>> 3. ```Multiplying polynomials```
+
+> ## Simplifying Alegebraic Expressions
+>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+
+> ## Factoring
+>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+>> (e.g 5x + 10 = 5(x + 2) ).
+
+>> |Type of Polynomial|Definition|
+>> |:-----------------|:---------|
+>> |Monomial|Polynomial that only has one term|
+>> |Binomial|Polynomial that only has 2 terms|
+>> |Trinomial|polynomial that only has 3 terms|
+
+>> |Type|Example|
+>> |:--:|:-----:|
+>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
+>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+
+> ## Shortcuts
+
+>>
+>> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+
+
+> ## Tips
+>> Watch out for the ```+/-``` signs
+>> Make sure to review your knowledge of the exponent laws
+>> For scientific notation, watch out for the decimal point
+>> Use shortcut when multiplying fractions
+
+
+# Polyomials (2)
+> ## Introduction to Polynomials
+>> A ```variable``` is a letter that represents one or more numbers
+>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
+>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+> ## Methods to solve a polynomial
+>> 1. ```Combine like terms```
+>> 2. ```Dividing polynomials```
+>> 3. ```Multiplying polynomials```
+
+> ## Simplifying Alegebraic Expressions
+>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+
+> ## Factoring
+>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+>> (e.g 5x + 10 = 5(x + 2) ).
+
+>> |Type of Polynomial|Definition|
+>> |:-----------------|:---------|
+>> |Monomial|Polynomial that only has one term|
+>> |Binomial|Polynomial that only has 2 terms|
+>> |Trinomial|polynomial that only has 3 terms|
+
+>> |Type|Example|
+>> |:--:|:-----:|
+>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
+>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+
+> ## Shortcuts
+
+>>  +
+> ## Foil / Rainbow Method
+>>
+
+> ## Foil / Rainbow Method
+>>  +
+> ## Definitions
+>> ```Term``` a variable that may have coefficient(s) or a constant
+>> ```Alebraic Expressions```: made up of one or more terms
+>> ```Like-terms```: same variables raised to the same exponent
+
+> ## Tips
+>> Be sure to factor fully
+>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+>> Remember your formulas
+>> Simplify first, combine like terms
+
+# Solving Equations and Inequailties (3)
+> ## Equations
+>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+>> To ```solve``` and equation is to find the variable that makes the statement true
+>> ### Methods to solve an equation
+>>> 1. Expand and simplify both sides
+>>> 2. Isolate using reverse order of operations
+>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+> ## Venn Diagrams
+
+>>
+
+> ## Definitions
+>> ```Term``` a variable that may have coefficient(s) or a constant
+>> ```Alebraic Expressions```: made up of one or more terms
+>> ```Like-terms```: same variables raised to the same exponent
+
+> ## Tips
+>> Be sure to factor fully
+>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+>> Remember your formulas
+>> Simplify first, combine like terms
+
+# Solving Equations and Inequailties (3)
+> ## Equations
+>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+>> To ```solve``` and equation is to find the variable that makes the statement true
+>> ### Methods to solve an equation
+>>> 1. Expand and simplify both sides
+>>> 2. Isolate using reverse order of operations
+>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+> ## Venn Diagrams
+
+>>  +
+>> ```Set```: a collection of elements, O (the circle)
+>> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
+>> ```Union```: ∪
+>> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
+>> ```Intersection```: ∩
+>> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
+>> ```Set Notation```:
+>> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
+>> ```Absolute Value```
+>>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>>> equations will have the absolute bracket be positive while the other negative.
+>>> Absolute values are written in the form ```| x |```
+>>> where
+>>> if x > 0, | x | = x
+>>> if x == 0, | x | = 0
+>>> if x < 0, | x | = -x
+
+> ## Quadractic Equations
+>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+>> Solve quadratic equation by:
+>> 1. Isolation
+>> a(x+b)2 + k = 0
+>> 2. Factor using zero-product property
+>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+>> (x-a)(x-b)=0
+>> x = a, b
+
+>>
+
+>> ```Set```: a collection of elements, O (the circle)
+>> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
+>> ```Union```: ∪
+>> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
+>> ```Intersection```: ∩
+>> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
+>> ```Set Notation```:
+>> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
+>> ```Absolute Value```
+>>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>>> equations will have the absolute bracket be positive while the other negative.
+>>> Absolute values are written in the form ```| x |```
+>>> where
+>>> if x > 0, | x | = x
+>>> if x == 0, | x | = 0
+>>> if x < 0, | x | = -x
+
+> ## Quadractic Equations
+>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+>> Solve quadratic equation by:
+>> 1. Isolation
+>> a(x+b)2 + k = 0
+>> 2. Factor using zero-product property
+>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+>> (x-a)(x-b)=0
+>> x = a, b
+
+>>  +
+>> Note:
+>> √x2 = ± x (There are 2 possible solutions)
+>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+>> ## Discriminant
+>>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+>>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
+>>> D = b2 - 4ac
+>>> D > 0 ```(2 distinct real solutions)```
+>>> D = 0 ```(1 real solution)```
+>>> D < 0 ```(no real solutions)```
+
+>>>
+
+>> Note:
+>> √x2 = ± x (There are 2 possible solutions)
+>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+>> ## Discriminant
+>>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+>>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
+>>> D = b2 - 4ac
+>>> D > 0 ```(2 distinct real solutions)```
+>>> D = 0 ```(1 real solution)```
+>>> D < 0 ```(no real solutions)```
+
+>>>  +
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>
+
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>  +
+> 2. ```Supplementary Angle Triangle``` (SAT)
+> - When two angles add up to 180 degrees
+
+>
+
+> 2. ```Supplementary Angle Triangle``` (SAT)
+> - When two angles add up to 180 degrees
+
+>  +
+> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
+> - Two lines intersect, two angles form opposite. They have equal measures
+
+>
+
+> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
+> - Two lines intersect, two angles form opposite. They have equal measures
+
+>  +
+> 4. ```Complementary Angle Theorem``` (CAT)
+> - The sum of two angles that add up to 90 degrees
+
+>
+
+> 4. ```Complementary Angle Theorem``` (CAT)
+> - The sum of two angles that add up to 90 degrees
+
+>  +
+> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+> - The sum of the three interior angles of any triangle is 180 degrees
+
+>
+
+> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+> - The sum of the three interior angles of any triangle is 180 degrees
+
+>  +
+> 6. ```Exterior Angle Theorem``` (EAT)
+> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+
+>
+
+> 6. ```Exterior Angle Theorem``` (EAT)
+> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+
+>  +
+> 7. ``` Isosceles Triangle Theorem``` (ITT)
+> - The base angles in any isosceles triangle are equal
+
+>
+
+> 7. ``` Isosceles Triangle Theorem``` (ITT)
+> - The base angles in any isosceles triangle are equal
+
+>  +
+> ## Properties of Quadrilaterals
+>> Determine the shape using the properties of it
+
+>> |Figure|Properties|
+>> |:-----|:---------|
+>> |Scalene Triangle|no sides equal|Length of line segment|
+>> |Isosceles Triangle| two sides equal|Length of line segment|
+>> |Equilateral Triangle|All sides equal|Length of line segment|
+>> |Right Angle Triangle|Two sides are perpendicular to each other|
+>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+>> |Kite|The diagonals are perpendicular|
+
+> ## 2D Geometry Equations
+>> |Shape|Formula|Picture|
+>> |:----|:------|:------|
+>> |Rectangle|```Area```: lw
+
+> ## Properties of Quadrilaterals
+>> Determine the shape using the properties of it
+
+>> |Figure|Properties|
+>> |:-----|:---------|
+>> |Scalene Triangle|no sides equal|Length of line segment|
+>> |Isosceles Triangle| two sides equal|Length of line segment|
+>> |Equilateral Triangle|All sides equal|Length of line segment|
+>> |Right Angle Triangle|Two sides are perpendicular to each other|
+>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+>> |Kite|The diagonals are perpendicular|
+
+> ## 2D Geometry Equations
+>> |Shape|Formula|Picture|
+>> |:----|:------|:------|
+>> |Rectangle|```Area```: lw  +
+> ## Median
+>> Each median divides the triangle into 2 smaller triangles of equal area
+>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
+>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
+
+>>
+
+> ## Median
+>> Each median divides the triangle into 2 smaller triangles of equal area
+>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
+>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
+
+>>  +
+> ## Terms:
+>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
+>>>
+
+> ## Terms:
+>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
+>>>  +>> ```Midpoint```: A point on a line where the length of either side of the point are equal
+>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+>> ```Centroid```: The intersection of the 3 medians of a triangle
+>>>
+>> ```Midpoint```: A point on a line where the length of either side of the point are equal
+>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+>> ```Centroid```: The intersection of the 3 medians of a triangle
+>>>  +
+> ## Proportionality theorem:
+>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+>>
+
+> ## Proportionality theorem:
+>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+>>  +
+
+> ## Definitions
+>> ```Parallel```: 2 lines with the same slope
+>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+>> ```Collinear Points```: points that line on the same straight line
+
+> ## Variables
+>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+> ## Statistics
+>> ```Interpolation```: Data **inside** the given data set range.
+>> ```Extrapolation```: Data **outside** the data set range.
+>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+>> and it represents the trend of a graph.
+>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+> ## Time - Distance Graph
+>> Time is the independent variable and distance is the dependent variable
+>> You can't go backwards on the x-axis, as you can't go back in time
+>> Plot the points accordingly
+>> Draw the lines accordingly
+>>
+
+
+> ## Definitions
+>> ```Parallel```: 2 lines with the same slope
+>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+>> ```Collinear Points```: points that line on the same straight line
+
+> ## Variables
+>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+> ## Statistics
+>> ```Interpolation```: Data **inside** the given data set range.
+>> ```Extrapolation```: Data **outside** the data set range.
+>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+>> and it represents the trend of a graph.
+>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+> ## Time - Distance Graph
+>> Time is the independent variable and distance is the dependent variable
+>> You can't go backwards on the x-axis, as you can't go back in time
+>> Plot the points accordingly
+>> Draw the lines accordingly
+>>  +
+> ## Scatterplot and Line of Best Fit
+>> A scatterplot graph is there to show the relation between two variables in a table of values.
+>> A line of best fit is a straight line that describes the relation between two variables.
+>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+>>
+
+> ## Scatterplot and Line of Best Fit
+>> A scatterplot graph is there to show the relation between two variables in a table of values.
+>> A line of best fit is a straight line that describes the relation between two variables.
+>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+>>  +
+> ## Table of values
+>> To find first differences or any points on the line, you can use a ```table of values```
+
+>>| y | x |First Difference|
+>>|:--|:--|:---------------|
+>>|-1|-2|1|
+>>|0|-1|1|
+>>|1|0|1|
+>>|2|1|1|
+>>|3|2|1|
+>>|4|3|1|
+
+> ## Tips
+>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+>> Draw your ```Line of Best Fit``` correctly
+>> Read the word problems carefully, and make sure you understand it when graphing things
+>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+>> Label your lines
+
+# System of Equations (6)
+
+> ## Linear System
+>> Two or more equation that you are working on all together at once on the same set of axes.
+>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+>> when **Profit = 0**. There is no gain or loss.
+
+>> ### Number of Solutions
+>>>
+
+> ## Table of values
+>> To find first differences or any points on the line, you can use a ```table of values```
+
+>>| y | x |First Difference|
+>>|:--|:--|:---------------|
+>>|-1|-2|1|
+>>|0|-1|1|
+>>|1|0|1|
+>>|2|1|1|
+>>|3|2|1|
+>>|4|3|1|
+
+> ## Tips
+>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+>> Draw your ```Line of Best Fit``` correctly
+>> Read the word problems carefully, and make sure you understand it when graphing things
+>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+>> Label your lines
+
+# System of Equations (6)
+
+> ## Linear System
+>> Two or more equation that you are working on all together at once on the same set of axes.
+>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+>> when **Profit = 0**. There is no gain or loss.
+
+>> ### Number of Solutions
+>>>  +
+> ## Tips
+>> Read the questions carefully and model the system of equations correctly
+>> Be sure to name your equations
+>> Label your lines
+
+# General Tips
+> Be sure to watch out for units, like ```cm``` or ```km```
+> Watch out for ```+/-```
+> Be sure to reverse the operation when moving things to the other side of the equation
+> Make sure to have a proper scale for graphs
+> Read question carefully and use the appropriate tools to solve
+> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+
+> ## Word Problems
+>> Read carefully
+>> model equations correctly
+>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+
+> ## Graph Problems
+>> Look up on tips in units (5) and (6)
+>> be sure to use a ruler when graphing
+
+> ## System of Equations
+>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+
+# Credits
+> Ryan Mark - He helped provide alot of information for me
+> Magicalsoup - ME!
+
+> ## Tips
+>> Read the questions carefully and model the system of equations correctly
+>> Be sure to name your equations
+>> Label your lines
+
+# General Tips
+> Be sure to watch out for units, like ```cm``` or ```km```
+> Watch out for ```+/-```
+> Be sure to reverse the operation when moving things to the other side of the equation
+> Make sure to have a proper scale for graphs
+> Read question carefully and use the appropriate tools to solve
+> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+
+> ## Word Problems
+>> Read carefully
+>> model equations correctly
+>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+
+> ## Graph Problems
+>> Look up on tips in units (5) and (6)
+>> be sure to use a ruler when graphing
+
+> ## System of Equations
+>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+
+# Credits
+> Ryan Mark - He helped provide alot of information for me
+> Magicalsoup - ME!