diff --git a/Grade 9/Math/MPM1DZ/Unit 6: System of Equations.md b/Grade 9/Math/MPM1DZ/Unit 6: System of Equations.md
new file mode 100644
index 0000000..6e077d8
--- /dev/null
+++ b/Grade 9/Math/MPM1DZ/Unit 6: System of Equations.md
@@ -0,0 +1,146 @@
+
+# Unit 6: System of Equations
+
+## Linear System
+- Two or more equation that you are working on all together at once on the same set of axes.
+- The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+- The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+- In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+- when **Profit = 0**. There is no gain or loss.
+
+### Number of Solutions
+- 
+
+## Discriminant
+- The discriminant determines the number of solutions (roots) there are in a quadratic equation. $`a, b , c`$ are the
+- coefficients and constant of a quadratic equation: $`y = ax^2 + bx + c`$
+ $`
+ D = b^2 - 4ac
+ \begin{cases}
+ \text{2 distinct real solutions}, & \text{if } D > 0 \\
+ \text{1 real solution}, & \text{if } D = 0 \\
+ \text{no real solutions}, & \text{if } D < 0
+ \end{cases}
+ `$
+
+- 
+
+## Solving Linear-Quadratic Systems
+- To find the point of intersection, do the following:
+ 1. Isolate both equations for $`y`$
+ 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+ 3. Simplify and put everything on one side and equal to zero on the other side
+ 4. Factor
+ 5. Use zero-product property to solve for all possible x-values
+ 6. Subsitute the x-values to one of the original equations to solve for all y-values
+ 7. State a conclusion / the solution
+
+- 
+
+- There are 3 possible cases
+- In addition, to determine the number of solutions, you the Discriminant formula $`D = b^2 - 4ac`$
+
+
+# Ways to solve Systems of Equations
+ ## 1. Subsitution
+ - Here we eliminate a variable by subbing in another variable from another equation
+ - We usually do this method if a variable is easily isolated
+ - Example:
+ - ```
+ y = x + 10 (1)
+ x + y + 34 = 40 (2)
+ ```
+ - We can sub $`(1)`$ into $`(2)`$ to find $`x`$, then you the value of $`x`$ we found to solve for $`y`$
+ ```
+ x + (x + 10) + 34 = 40
+ 2x + 44 = 40
+ 2x = -4
+ x = -2
+ ```
+ - Then solve for $`y`$
+ ```
+ y = -2 + 10
+ y = -8
+ ```
+
+ ## 2. Elimination
+ - Here we eliminate a variable by basically eliminate a variable from an equation
+ - We usually use this method first when the variables are not easily isolated, then use subsitution to solve
+ - Example:
+ - ```
+ 2x + 3y = 10 (1)
+ 4x + 3y = 14 (2)
+ ```
+ - We can then use elimination
+ ```
+ 4x + 3y = 14
+ 2x + 3y = 10
+ ------------
+ 2x + 0 = 4
+ x = 2
+ ```
+ - Then sub the value of $`x`$ into an original equation and solve for $`y`$
+ ```
+ 2(2) + 3y = 10
+ 3y = 6
+ y = 2
+ ```
+
+## 3. Graphing
+ - we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
+
+## Solving Systems of Linear Inequalities
+- Find the intersection region as the ```solution```.
+- ## If
+
+ - | |Use ```Dash``` line|Use ```Solid line```|
+ |:-|:------------------|:-------------------|
+ |Shade the region ```above``` the line|$`y > mx + b`$|$`y \ge mx + b`$|
+ |Shade the region ```below``` the line|$`y < mx + b`$|$`y \le mx + b`$|
+
+- ## If
+
+ - |$`x > a`$
$`x \ge a`$|
+ |:------------------|
+ |shade the region on the **right**|
+
+- ## If
+
+ - |$`x < a`$
$`x \le a`$|
+ |:------------------|
+ |shade the region on the **left**|
+
+- Step 1. change all inequalities to ```y-intercept form```
+- Step 2. graph the line
+- Step 3. shade the region where all the regions overlap
+
+- 
+
+
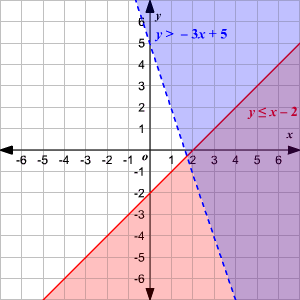+## Tips
+- Read the questions carefully and model the system of equations correctly
+- Be sure to name your equations
+- Label your lines
+
+# General Tips
+- Be sure to watch out for units, like ```cm``` or ```km```
+- Watch out for ```+/-```
+- Be sure to reverse the operation when moving things to the other side of the equation
+- Make sure to have a proper scale for graphs
+- Read question carefully and use the appropriate tools to solve
+- **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+
+## Word Problems
+- Read carefully
+- model equations correctly
+- ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+- ```Lets``` Statement
+- ```Conclusion```
+
+## Graph Problems
+- Look up on tips in units (5) and (6)
+- be sure to use a ruler when graphing
+
+## System of Equations
+- When in doubt or to check your work, just plug the numbers back in and check if the statement is true
\ No newline at end of file