diff --git a/Grade 9/Math/MFM1P1/Final_Exam_Study_Sheet.md b/Grade 9/Math/MFM1P1/Final_Exam_Study_Sheet.md
index dadea5e..6278be7 100644
--- a/Grade 9/Math/MFM1P1/Final_Exam_Study_Sheet.md
+++ b/Grade 9/Math/MFM1P1/Final_Exam_Study_Sheet.md
@@ -1,5 +1,6 @@
# Study Sheet
+# Unit 1: Diagnostic & Essential Number Skills
## Rounding and Decimals
### Decimals
@@ -162,5 +163,138 @@
- Then change the division to a multiply: $`\frac{4}{2} \times \frac{9}{6}`$
- Then multiply the 2 fractions $`\frac{4 \times 9}{2 \times 6} = \frac{36}{12}`$
+# Unit 2: Measurement
+
+## Measuring Perimeter and Area
+
+### 2D Shapes
+ |Shape|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangle|```Area```: $`lw`$
```Perimeter```: $`2(l+w)`$|
|
+ |Triangle|```Area```: $`\frac{bh}{2}`$
```Perimeter```: $`a+b+c`$|
|
+ |Circle|```Area```: $`πr^2`$
```Circumference```: $`2πr`$ or $`πd`$|
|
+ |Trapezoid|```Area```: $` \frac{(a+b)h}{2}`$
```Perimeter```: $`a+b+c+d`$|
|
+
+## Right Triangle and Pythagorean Theorem
+
+- `a` and `b` are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, `c` is the hypotenuse
+- $`a^2+b^2=c^2`$
+
+- 
+
+## Area of Composite Figures
+- You can cut any normal polygon into standard polygons you know, for example, a polygon shaped as a house can be split into a recntalge and a triangle. All normal polygon, can be simplified into triangles.
+
+## Perimeter of Composite Figures
+- Same as an area of composite figures, cut them down into much simplified shapes so you can easily calculate its area. Alternatively, if its possible, you can even measure the shape using a tool such as ruler.
+
+### 3D Objects
+|3D Object|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangular Prism|```Volume```: $`lwh`$
```SA```: $`2(lw+lh+wh)`$|
|
+ |Square Based Pyramid|```Volume```: $`\frac{1}{3} b^2 h`$
```SA```: $`2bs+b^2`$|
|
+ |Sphere|```Volume```: $`\frac{4}{3} πr^3`$
```SA```: $`4πr^2`$|
|
+ |Cone|```Volume```: $` \frac{1}{3} πr^2 h`$
```SA```: $`πrs+πr^2`$|
|
+ |Cylinder|```Volume```: $`πr^2h`$
```SA```: $`2πr^2+2πh`$|
|
+ |Triangular Prism|```Volume```: $`ah+bh+ch+bl`$
```SA```: $` \frac{1}{2} blh`$|
|
+
+# Unit 3: Optimization
+
+## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
+
+### 2D Shapes
+
+ |Shape|Maximum Area|Minimum Perimeter|
+ |:----|:-----------|:----------------|
+ |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
$`A = lw`$
$`A_{max} = (w)(w)`$
$`A_{max} = w^2`$|A rectangle must be a square to minimaze the perimeter for a given area. The length is equal to the width.
$`P = 2(l+w)`$
$`P_{min} = 2(w)(w)`$
$`P_{min} = 2(2w)`$
$`P_{min} = 4w`$|
+ |3-sided rectangle|$`l = 2w`$
$`A = lw`$
$`A_{max} = 2w(w)`$
$`A_{max} = 2w^2`$|$`l = 2w`$
$`P = l+2w`$
$`P_{min} = 2w+2w`$
$`P_{min} = 4w`$|
+
+# Unit 4: Relationship in Geometry
+
+## Angle Theorems
+
+### 1. Transversal Parallel Line Theorems (TPT)
+ a. Alternate Angles are Equal ```(Z-Pattern)```
+ b. Corresponding Angles Equal ```(F-Pattern)```
+ c. Interior Angles add up to 180 ```(C-Pattern)```
+
+> 
+
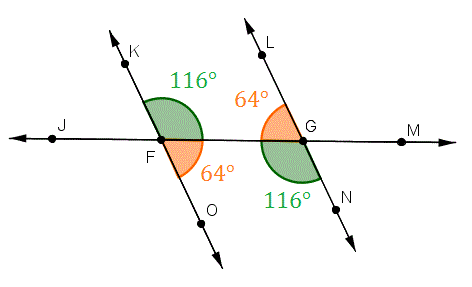+### 2. Supplementary Angle Triangle (SAT)
+ - When two angles add up to 180 degrees
+
+ - 
+
+### 3. Opposite Angle Theorem (OAT) (OAT)
+ - Two lines intersect, two angles form opposite. They have equal measures
+
+ - 
+
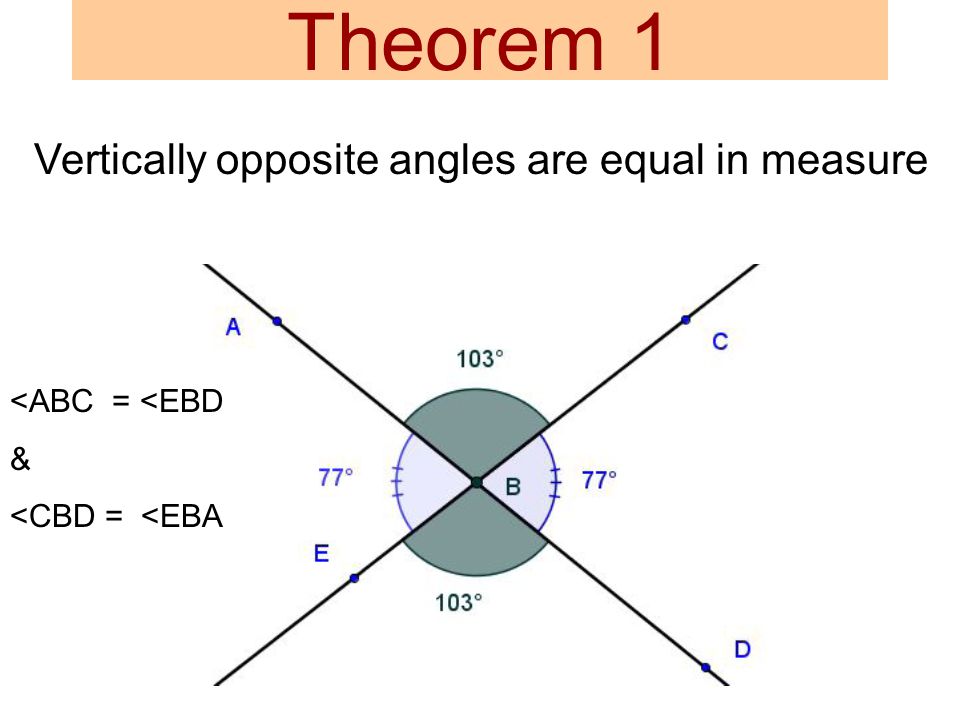+### 4. Complementary Angle Theorem (CAT)
+ - The sum of two angles that add up to 90 degrees
+
+ - 
+
+### 5. Angle Sum of a Triangle Theorem (ASTT)
+ - The sum of the three interior angles of any triangle is 180 degrees
+
+ - 
+
+### 6. Exterior Angle Theorem (EAT)
+ - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+
+ -
+
+### 7. Isosceles Triangle Theorem (ITT)
+ - The base angles in any isosceles triangle are equal
+
+ - 
+
+### 8. Sum of The Interior Angle of a Polygon
+ - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+
+ - 
+
+
+### 9. Exterior Angles of a Convex Polygon
+ - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+
+ - 
+
+# Unit 5: Proportional Reasoning
+
+## Equivalent Ratios
+- An easy way to see if ratios are equivalent is to see if the ratios are the same in its simpliest form. A ratio is a fraction in essence, the first number is the `numerator`, and the second number is the `demominator`.
+
+- An easy way to find an equivalent ratio is just to multiply the everything by 2, for example, given a ratio `2:5`, multiply everything by 2, so your new ratio will be `2x2:5x2 = 4:10`.
+
+## Ratio and Proportions
+- Ratios link directly with proportions, as a ratio of one thing can be applied to another ratio of another thing.
+- Example
+ - Given one ratio of one triangle's height to base and another ratio of another triangle's heigth to base, we can find one missing side length given that we have the other 3.
+ - Lets say the 2 ratios are `1:5` and `3:x`, given that `x` is a random number.
+ - To solve `x`, we can cross-multiply, or multipling the `numerators` with the `denominators` and setting them equal to each other. Thus, we can first make the ratios into fractions and then do: $`\frac{1}{5} \text{ cross-multiply } \frac{3}{x} \rightarrow 1x = 3 \times 5`$. Which we can then solve for `x`, which is `15`.
+
+
+## Solving Algebraic Equations
+- To solve equations, just remove the extra bits on both sides by doing the opposite. So if its addition, do subraction to get rid of the added numbers, and vice versa:
+
+|Example|To solve:|
+|:------|:--------|
+|$`x + 3 = 15`$|$`(x + 3)-3 = 15-3`$
$`x = 12`$|
+|$`x - 3 = 15`$|$`(x - 3)+3 = 15+3`$
$`x = 18`$|
+|$`x \div 3 = 15`$|$`(\frac{x}{3}) \times 3 = 15 \times 3`$
$`x = 45`$|
+|$`x \times 3 = 15`$|$`\frac{x \times 3}{3} = \frac{15}{3}`$
$`x = 5`$|
+
+
+## Fraction to Decimal
+- Simply divide the `numerator` by the `denominator`. So $`\frac{3}{4} = 3 \div 4, \text{or } 0.75`$.
+## Fraction to Percent
+- The percentage symbol `%`, means the number has been multiplied by 100, so given a fraction $`\frac{3}{4}`$, convert the fraction into a decimal. Then multiply that decimal by `100`.
+- $`\frac{3}{4} = 0.75 \rightarrow 0.75 \times 100 = 75\%`$
+
+## Percent as a Ratio
+- Simply divide the first number by the second number, and multiply by one `100`. It is the same as making the ratio into a fraction, then converting the fraction into a percentage.
+
\ No newline at end of file