From 4fb1832fa1aa098f1c41abe745d6e2d18a04b2f9 Mon Sep 17 00:00:00 2001
From: Soup <39444003+magicalsoup@users.noreply.github.com>
Date: Tue, 15 Jan 2019 13:58:50 -0500
Subject: [PATCH] Update Math.md
---
Grade 9/Math.md | 131 +++++++++++++++++++++++++++---------------------
1 file changed, 73 insertions(+), 58 deletions(-)
diff --git a/Grade 9/Math.md b/Grade 9/Math.md
index 651c255..e43cd6d 100644
--- a/Grade 9/Math.md
+++ b/Grade 9/Math.md
@@ -53,7 +53,7 @@
>> | a ∩ b | Intersection (and) |
> ## Pythgorean Theorem
->> let a be the adjecant and b be the opposite, and c be the hypotenuse.
+>> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
>> a2 + b2 = c2
>>  @@ -68,10 +68,10 @@
>> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
>> To Divide rationals, multiply them by the reciprocal
>> ### Example Simplify Fully:
->>> = 3⁄4 ÷ 2⁄12 [Reduce to lowest terms]
->>> = 3⁄4 ÷ 1⁄7 [Multiply by reciprocal]
->>> = 3⁄4 × 7
->>> = 21⁄4 [Leave as an improper fraction]
+>>> =
@@ -68,10 +68,10 @@
>> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
>> To Divide rationals, multiply them by the reciprocal
>> ### Example Simplify Fully:
->>> = 3⁄4 ÷ 2⁄12 [Reduce to lowest terms]
->>> = 3⁄4 ÷ 1⁄7 [Multiply by reciprocal]
->>> = 3⁄4 × 7
->>> = 21⁄4 [Leave as an improper fraction]
+>>> =  [Reduce to lowest terms]
+>>> =
[Reduce to lowest terms]
+>>> =  [Multiply by reciprocal]
+>>> =
[Multiply by reciprocal]
+>>> =  × 7
+>>> =
× 7
+>>> = 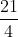 [Leave as an improper fraction]
>> ### Shortcut for multiplying fractions
>>> cross divide to keep your numbers small
@@ -93,7 +93,7 @@
>>> |Rational Exponents|an/m = (m√a)n|165/4 = (4√16)5 = 25|
>>> **Note:**
->>> Standard --> Expanded Form
+>>> Exponential Form --> Expanded Form
>>> 64 = 6 × 6 × 6 × 6
>> ## Scientific Notation
@@ -188,26 +188,16 @@
>>> 1. Expand and simplify both sides
>>> 2. Isolate using reverse order of operations
>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
-> ## Venn Diagrams
-
->>
[Leave as an improper fraction]
>> ### Shortcut for multiplying fractions
>>> cross divide to keep your numbers small
@@ -93,7 +93,7 @@
>>> |Rational Exponents|an/m = (m√a)n|165/4 = (4√16)5 = 25|
>>> **Note:**
->>> Standard --> Expanded Form
+>>> Exponential Form --> Expanded Form
>>> 64 = 6 × 6 × 6 × 6
>> ## Scientific Notation
@@ -188,26 +188,16 @@
>>> 1. Expand and simplify both sides
>>> 2. Isolate using reverse order of operations
>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
-> ## Venn Diagrams
-
->> 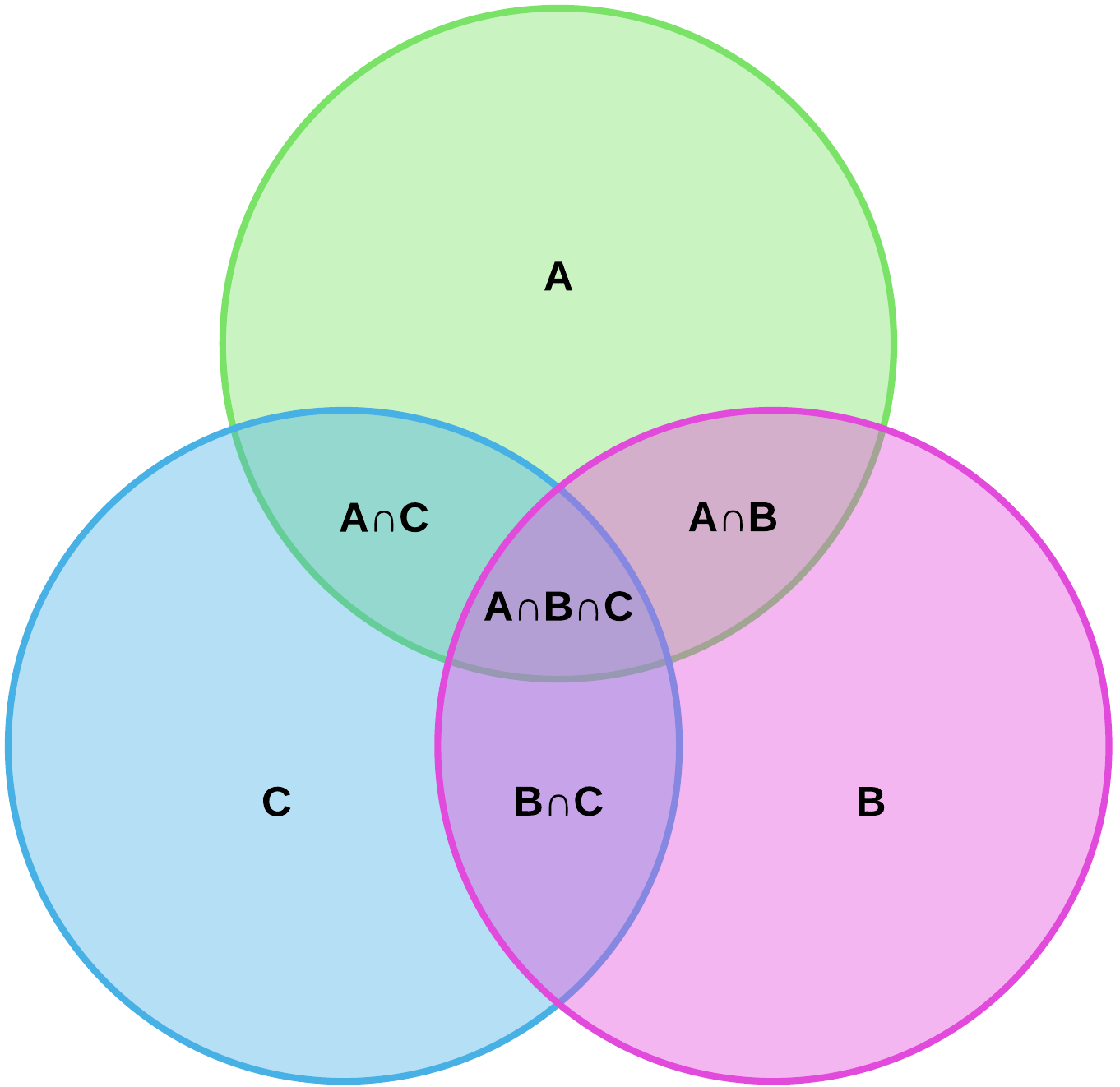 -
->> ```Set```: a collection of elements, O (the circle)
->> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
->> ```Union```: ∪
->> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
->> ```Intersection```: ∩
->> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
->> ```Set Notation```:
->> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
->> ```Absolute Value```
->>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->>> equations will have the absolute bracket be positive while the other negative.
->>> Absolute values are written in the form ```| x |```
->>> where
->>> if x > 0, | x | = x
->>> if x == 0, | x | = 0
->>> if x < 0, | x | = -x
+
+>
+> ## Absolute Values
+>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>> equations will have the absolute bracket be positive while the other negative.
+>> Absolute values are written in the form ```| x |```
+>> where
+>> if x > 0, | x | = x
+>> if x = 0, | x | = 0
+>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
@@ -225,31 +215,7 @@
>> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
->> ## Discriminant
->>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
->>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
->>> D = b2 - 4ac
->>> D > 0 ```(2 distinct real solutions)```
->>> D = 0 ```(1 real solution)```
->>> D < 0 ```(no real solutions)```
-
->>>
-
->> ```Set```: a collection of elements, O (the circle)
->> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
->> ```Union```: ∪
->> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
->> ```Intersection```: ∩
->> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
->> ```Set Notation```:
->> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
->> ```Absolute Value```
->>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->>> equations will have the absolute bracket be positive while the other negative.
->>> Absolute values are written in the form ```| x |```
->>> where
->>> if x > 0, | x | = x
->>> if x == 0, | x | = 0
->>> if x < 0, | x | = -x
+
+>
+> ## Absolute Values
+>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>> equations will have the absolute bracket be positive while the other negative.
+>> Absolute values are written in the form ```| x |```
+>> where
+>> if x > 0, | x | = x
+>> if x = 0, | x | = 0
+>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
@@ -225,31 +215,7 @@
>> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
->> ## Discriminant
->>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
->>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
->>> D = b2 - 4ac
->>> D > 0 ```(2 distinct real solutions)```
->>> D = 0 ```(1 real solution)```
->>> D < 0 ```(no real solutions)```
-
->>>  -
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->
-
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->  -
-> There are 3 possible cases
-> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
-
+
> ## Tips
>> ```Absolute Values``` can have 2 solutions
>> ```Quadratics``` can also have 2 solutions
@@ -292,10 +258,22 @@
>
-
-> There are 3 possible cases
-> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
-
+
> ## Tips
>> ```Absolute Values``` can have 2 solutions
>> ```Quadratics``` can also have 2 solutions
@@ -292,10 +258,22 @@
>  > 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+> - The base angles in any isosceles triangle are equal
>
> 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+> - The base angles in any isosceles triangle are equal
>  +> 8. ```Sum of The Interior Angle of a Polygon```
+> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+
+
+> 8. ```Sum of The Interior Angle of a Polygon```
+> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+
+ +
+
+> 9. ```Exterior Angles of a Convex Polygon```
+> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+
+
+
+
+> 9. ```Exterior Angles of a Convex Polygon```
+> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+
+ +
+
> ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
@@ -392,8 +370,8 @@
> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
> ## Slope and Equation of Line
->> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```change in y / change in x```
->> ```Slope Formula```: **m = y2-y1/x2-x1**
+>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```rate of change y / rate of change x```
+>> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
>> ```Y-intercept Form```: **y = mx + b**
>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
@@ -412,8 +390,8 @@
>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
>> degrees and **h** is the depth in meters.
-> ## Perpendicular Bisector
->> To find the perpendicular bisector, you will need to fidn the slope and midpoint
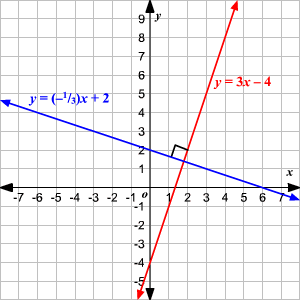
+> ## Perpendicular Lines
+>> To find the perpendicular slope, you will need to find the slope point
>> Formula: slope1 × slope2 = -1
>> Notation: m⊥
>>
+
+
> ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
@@ -392,8 +370,8 @@
> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
> ## Slope and Equation of Line
->> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```change in y / change in x```
->> ```Slope Formula```: **m = y2-y1/x2-x1**
+>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```rate of change y / rate of change x```
+>> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
>> ```Y-intercept Form```: **y = mx + b**
>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
@@ -412,8 +390,8 @@
>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
>> degrees and **h** is the depth in meters.
-> ## Perpendicular Bisector
->> To find the perpendicular bisector, you will need to fidn the slope and midpoint
+> ## Perpendicular Lines
+>> To find the perpendicular slope, you will need to find the slope point
>> Formula: slope1 × slope2 = -1
>> Notation: m⊥
>>  @@ -446,13 +424,24 @@
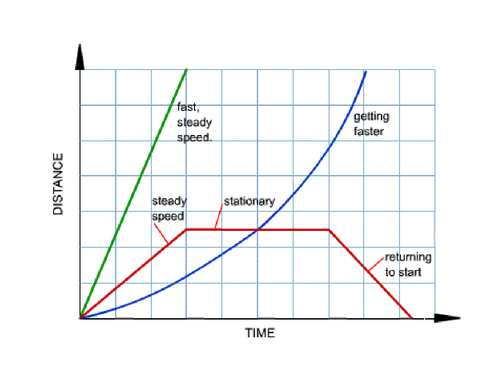
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
->>
@@ -446,13 +424,24 @@
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
->>  +>>
+>>  +
+>> **Direction is always referring to:**
+
+>> 1. ```go towards home```
+>> 2. ```going away from home```
+>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>
+
+>> **Direction is always referring to:**
+
+>> 1. ```go towards home```
+>> 2. ```going away from home```
+>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>  +>>
+>>  +
+>> ### How To Determine the Equation Of a Line of Best Fit
+>> 1. Find two points **```ON```** the ```line of best fit```
+>> 2. Determine the ```slope``` using the two points
+>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
@@ -486,6 +475,32 @@
>> ### Number of Solutions
>>>
+
+>> ### How To Determine the Equation Of a Line of Best Fit
+>> 1. Find two points **```ON```** the ```line of best fit```
+>> 2. Determine the ```slope``` using the two points
+>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
@@ -486,6 +475,32 @@
>> ### Number of Solutions
>>>  +> ## Discriminant
+>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
+>> D = b2 - 4ac
+>> D > 0 ```(2 distinct real solutions)```
+>> D = 0 ```(1 real solution)```
+>> D < 0 ```(no real solutions)```
+
+>>
+> ## Discriminant
+>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
+>> D = b2 - 4ac
+>> D > 0 ```(2 distinct real solutions)```
+>> D = 0 ```(1 real solution)```
+>> D < 0 ```(no real solutions)```
+
+>>  +
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>>
+
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>>  +
+>> There are 3 possible cases
+>> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
+
+
> # Ways to solve Systems of Equations
> 1. Subsitution
> Here we eliminate a variable by subbing in another variable from another equation
+
+>> There are 3 possible cases
+>> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
+
+
> # Ways to solve Systems of Equations
> 1. Subsitution
> Here we eliminate a variable by subbing in another variable from another equation
 -
->> ```Set```: a collection of elements, O (the circle)
->> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
->> ```Union```: ∪
->> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
->> ```Intersection```: ∩
->> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
->> ```Set Notation```:
->> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
->> ```Absolute Value```
->>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->>> equations will have the absolute bracket be positive while the other negative.
->>> Absolute values are written in the form ```| x |```
->>> where
->>> if x > 0, | x | = x
->>> if x == 0, | x | = 0
->>> if x < 0, | x | = -x
+
+>
+> ## Absolute Values
+>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>> equations will have the absolute bracket be positive while the other negative.
+>> Absolute values are written in the form ```| x |```
+>> where
+>> if x > 0, | x | = x
+>> if x = 0, | x | = 0
+>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
@@ -225,31 +215,7 @@
>> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
->> ## Discriminant
->>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
->>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
->>> D = b2 - 4ac
->>> D > 0 ```(2 distinct real solutions)```
->>> D = 0 ```(1 real solution)```
->>> D < 0 ```(no real solutions)```
-
->>>
-
->> ```Set```: a collection of elements, O (the circle)
->> ```Universal Set```: This is a collection of all the elements that you are interested in. Use ```{}``` bracket to write the set inside the rectangle
->> ```Union```: ∪
->> if 2 sets have union, all the elements belong to any of the set. This is known as ```or```
->> ```Intersection```: ∩
->> if 2 sets have an intersection, they are elements belonging to both sets. This is known as ```and```
->> ```Set Notation```:
->> A notation that represents the collection of numbers. It is written in this form x = {x|x∈R}
->> ```Absolute Value```
->>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->>> equations will have the absolute bracket be positive while the other negative.
->>> Absolute values are written in the form ```| x |```
->>> where
->>> if x > 0, | x | = x
->>> if x == 0, | x | = 0
->>> if x < 0, | x | = -x
+
+>
+> ## Absolute Values
+>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+>> equations will have the absolute bracket be positive while the other negative.
+>> Absolute values are written in the form ```| x |```
+>> where
+>> if x > 0, | x | = x
+>> if x = 0, | x | = 0
+>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
@@ -225,31 +215,7 @@
>> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
->> ## Discriminant
->>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
->>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
->>> D = b2 - 4ac
->>> D > 0 ```(2 distinct real solutions)```
->>> D = 0 ```(1 real solution)```
->>> D < 0 ```(no real solutions)```
-
->>>  -
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->
-
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->  > 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+> - The base angles in any isosceles triangle are equal
>
> 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+> - The base angles in any isosceles triangle are equal
>  +> 8. ```Sum of The Interior Angle of a Polygon```
+> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+
+
+> 8. ```Sum of The Interior Angle of a Polygon```
+> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+
+ +
+
+> 9. ```Exterior Angles of a Convex Polygon```
+> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+
+
+
+
+> 9. ```Exterior Angles of a Convex Polygon```
+> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+
+ +
+
> ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
@@ -392,8 +370,8 @@
> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
> ## Slope and Equation of Line
->> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```change in y / change in x```
->> ```Slope Formula```: **m = y2-y1/x2-x1**
+>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```rate of change y / rate of change x```
+>> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
>> ```Y-intercept Form```: **y = mx + b**
>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
@@ -412,8 +390,8 @@
>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
>> degrees and **h** is the depth in meters.
-> ## Perpendicular Bisector
->> To find the perpendicular bisector, you will need to fidn the slope and midpoint
+> ## Perpendicular Lines
+>> To find the perpendicular slope, you will need to find the slope point
>> Formula: slope1 × slope2 = -1
>> Notation: m⊥
>>
+
+
> ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
@@ -392,8 +370,8 @@
> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
> ## Slope and Equation of Line
->> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```change in y / change in x```
->> ```Slope Formula```: **m = y2-y1/x2-x1**
+>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```rate of change y / rate of change x```
+>> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
>> ```Y-intercept Form```: **y = mx + b**
>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
@@ -412,8 +390,8 @@
>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
>> degrees and **h** is the depth in meters.
-> ## Perpendicular Bisector
->> To find the perpendicular bisector, you will need to fidn the slope and midpoint
+> ## Perpendicular Lines
+>> To find the perpendicular slope, you will need to find the slope point
>> Formula: slope1 × slope2 = -1
>> Notation: m⊥
>>  @@ -446,13 +424,24 @@
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
->>
@@ -446,13 +424,24 @@
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
->>  +>>
+>>  +
+>> **Direction is always referring to:**
+
+>> 1. ```go towards home```
+>> 2. ```going away from home```
+>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>
+
+>> **Direction is always referring to:**
+
+>> 1. ```go towards home```
+>> 2. ```going away from home```
+>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>  +>>
+>>  +
+>> ### How To Determine the Equation Of a Line of Best Fit
+>> 1. Find two points **```ON```** the ```line of best fit```
+>> 2. Determine the ```slope``` using the two points
+>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
@@ -486,6 +475,32 @@
>> ### Number of Solutions
>>>
+
+>> ### How To Determine the Equation Of a Line of Best Fit
+>> 1. Find two points **```ON```** the ```line of best fit```
+>> 2. Determine the ```slope``` using the two points
+>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
@@ -486,6 +475,32 @@
>> ### Number of Solutions
>>>  +
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>>
+
+> ## Solving Linear-Quadratic Systems
+>> To find the point of intersection, do the following:
+>> 1. Isolate both equations for ```y```
+>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+>> 3. Simplify and put everything on one side and equal to zero on the other side
+>> 4. Factor
+>> 5. Use zero-product property to solve for all possible x-values
+>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
+>> 7. State a conclusion / the solution
+
+>>