diff --git a/Grade 9/Math/MCF3M1/Final_Exam_Study_Sheet.md b/Grade 9/Math/MCF3M1/Final_Exam_Study_Sheet.md index a7ec9a0..78ee869 100644 --- a/Grade 9/Math/MCF3M1/Final_Exam_Study_Sheet.md +++ b/Grade 9/Math/MCF3M1/Final_Exam_Study_Sheet.md @@ -1,6 +1,6 @@ # Study Sheet -# Unit 1 +# Unit 1: Functions ## Words to know: @@ -11,3 +11,220 @@ - `axis of symmetry of a parabola` - `intercepts` + +- ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant +- ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant + + +## Relations +- A relation can be described using + 1. Table of Values (see below) + 2. Equations $`(y = 3x + 5)`$ + 3. Graphs (Graphing the equation) + 4. Words +- When digging into the earth, the temperature rises according to the +- following linear equation: $`t = 15 + 0.01 h`$. $`t`$ is the increase in temperature in +- degrees and $`h`$ is the depth in meters. + + + +## Definitions +- ```Parallel```: 2 lines with the same slope +- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet. +- ```Domain```: The **ordered** set of all possible values of the independent variable $`x`$. +- ```Range```: The **ordered** set of all possible values of the dependent variable $`y`$. +- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```. +- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```. +- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant. +- ```Collinear Points```: points that line on the same straight line + +## Variables +- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything. +- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable. + + +## Scatterplot and Line of Best Fit +- A scatterplot graph is there to show the relation between two variables in a table of values. +- A line of best fit is a straight line that describes the relation between two variables. +- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line. +- + +### How To Determine the Equation Of a Line of Best Fit + 1. Find two points **```ON```** the ```line of best fit``` + 2. Determine the ```slope``` using the two points + 3. Use ```point-slope form``` to find the equation of the ```line of best fit``` + +## Table of values +- To find first differences or any points on the line, you can use a ```table of values``` +- It shows the relationship between the x and y values. +- Use `Finite differences` to figure out if its quadraic or linear: + - If the `first difference` is constant, then its linear. (degree of 1) + - If the `second difference` is constant, then its quadratic. (degree of 2) + +- This is a linear function + + |x |y |First difference| + |:-|:-|:---------------| + |-3|5|$`\cdots`$| + |-2|7|5-7 = 2| + |-1|9|7-9 = 2| + |0|11|9-11 = 2| + |1|13|11-13 = 2| + |2|15|15-13 =2| + - The difference between the first and second y values are the same as the difference between the third and fourth. The `first difference` is constant. + +- This is a quadractic function + + |x |y |First difference|Second difference| + |:-|:-|:---------------|:----------------| + |5|9|$`\cdots`$|$`\cdots`$| + |7|4|9-4 = 5|$`\cdots`$| + |9|1|4-1 = 3|5-3 = 2| + |11|0|1-0 = 1|3 - 1 = 2| + |13|1|0-1 = -1|1 -(-1) = 2| + + - The difference between the differences of the first and second y values are the same as the difference of the difference between the thrid and fourth. The `second difference` is constant. + + + + + + +## Tips +- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis``` +- Draw your ```Line of Best Fit``` correctly +- Read the word problems carefully, and make sure you understand it when graphing things +- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience) +- Label your lines + + +### Number of Solutions +- + +## Discriminant +- The discriminant determines the number of solutions (roots) there are in a quadratic equation. $`a, b , c`$ are the +- coefficients and constant of a quadratic equation: $`y = ax^2 + bx + c`$ + $` + D = b^2 - 4ac + \begin{cases} + \text{2 distinct real solutions}, & \text{if } D > 0 \\ + \text{1 real solution}, & \text{if } D = 0 \\ + \text{no real solutions}, & \text{if } D < 0 + \end{cases} + `$ + +- + + +### Tips +- Read the questions carefully and model the system of equations correctly +- Be sure to name your equations +- Label your lines + + +## Definitions + - `Function`: a relation which there is only one value of the dependent variable for each value of the independent variable (i.e, for every x-value, there is only one y-value). + - `Vertical-line test`: a test to determine whether the graph of a relation is a function. The relation is not a function if at least one vertical line drawn through the graph of the relation passes through two or more points. + - `Real numbers`: the set of real numbers is the set of all decimals - positive, negative and 0, terminating and non-terminating. This statement is expressed mathematically with the set notation $`\{x \in \mathbb{R}\} `$ + - `Degree`: the degree of a polynomial with a single varible, say $`x`$, is the value of the highest exponent of the variable. For example, for the polynomial $`5x^3-4x^2+7x-8`$, the highest power or exponent is 3; the degree of the polynomial is 3. + - `Function notation`: $`(x, y) = (x f(x))`$. $`f(x)`$ is called function notation and represents the value of the dependent variable for a given value of the independent variable $`x`$. +- `Transformations`: transformation are operations performed on functions to change the position or shape of the associated curves or lines. + +## Working with Function Notation +- Given an example of $`f(x) = 2x^2+3x+5`$, to get $`f(3)`$, we substitute the 3 as $`x`$ into the function, so it now becomses $`f(3) = 2(3)^2+3(3)+5`$. +- We can also represent new functions, the letter inside the brackets is simply a variable, we can change it. + - Given the example $`g(x) = 2x^2+3x+x`$, if we want $`g(m)`$, we simply do $`g(m) = 2m^2+3m+m`$. + +## Vertex Form +- `Vertex from`: $`f(x) = a(x-h)^2 + k`$. 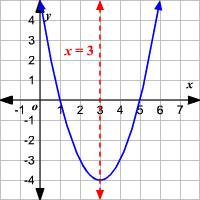+ - $`(-h, k)`$ is the coordinates of the vertex + +## Axis of symmetry +- $`x = -h`$ +- Example: + - $`f(x) = 2(x-3)^2+7`$ + - $`x = +3`$ + - + + +## Direction of openning $`\pm a`$ +- Given a quadratic in the from $`f(x) = ax^2+bx+c`$, if $`a > 0`$, the curve is a happy face, a smile. If $`a < 0`$, the curve is a sad face, a sad frown. +- $` + \text{Opening} = + \begin{cases} + \text{if } a > 0, & \text{opens up} \\ + \text{if } a < 0, & \text{opens down} + \end{cases} + `$ +- Examples + - $`f(x) = -5x^2`$ opens down, sad face. + - $`f(x) = 4(x-5)^2+7`$ opens up, happy face. + +## Vertical Translations $`\pm k`$ +- $` + \text{Direction} = + \begin{cases} + \text{if } k > 0, & \text{UP }\uparrow \\ + \text{if } k < 0, & \text{DOWN } \downarrow + \end{cases} + `$ + +## Horizontal Translations $`\pm h`$ +- $` + \text{Direction} = + \begin{cases} + \text{if } -h > 0, & \text{shift to the right} \\ + \text{if } -h < 0, & \text{shift to the left} + \end{cases} + `$ + +- $`f(x) = 1(x-4)^2`$ + - $`\uparrow`$ congruent to $`f(x) = x^2`$ + - +## Vertical Stretch/Compression +- $`|a|\leftarrow`$: absolute bracket. + - simplify and become positive +- $` + \text{Stretch/Compression} = + \begin{cases} + \text{if } |a| > 1, & \text{stretch by a factor of } a \\ + \text{if } 0 < |a| < 1, & \text{compress by a factor of } a + \end{cases} + `$ + - (Multiply all the y-values from $`y = x^2`$ by a) + - (Not congruent to $`f(x) = x^2`$) +- Example of stretching + - $`f(x) = 2x^2`$ + -Vertically stretch by a factor of 2 + - |x |y | + |:-|:-| + |-3|9`(2)` = 18| + |-2|4`(2)` = 8| + |-1|1`(2)`= 2| + |0|0`(2)` = 0| + |1|1`(2)` = 2| + |2|4`(2)`= 8| + |3|9`(2)` = 18| + + - All y-values from $`f(x) =x^2`$ are now multiplied by 2 to create $`f(x)=2x^2`$ + +- Example of compression + - $`f(x) = \frac{1}{2}x^2`$ + - Verticallyc ompressed by a factor of $`\frac{1}{2}`$ + - |x |y | + |:-|:-| + |-3|9$`(\frac{1}{2})`$ = 4.5| + |-2|4$`(\frac{1}{2})`$ = 2| + |-1|1$`(\frac{1}{2})`$ = $`\frac{1}{2}`$| + |0|0$`(\frac{1}{2})`$ = 0| + |1|1$`(\frac{1}{2})`$ = 1| + |2|4$`(\frac{1}{2})`$= $`\frac{1}{2}`$| + |3|9$`(\frac{1}{2})`$ = 4.5| + + - All y-values from $`f(x) = x^2`$ are now multiplied by $`\frac{1}{2}`$ to create $`f(x) = \frac{x^2}{2}`$ + + + + + +