diff --git a/Grade 9/Math/MPM1DZ/Final_Exam_Study_Sheet.md b/Grade 9/Math/MPM1DZ/Final_Exam_Study_Sheet.md
index 201e18a..78cfebe 100644
--- a/Grade 9/Math/MPM1DZ/Final_Exam_Study_Sheet.md
+++ b/Grade 9/Math/MPM1DZ/Final_Exam_Study_Sheet.md
@@ -1,637 +1,643 @@
# Math Study Sheet!!!!
# Exam Detail
-> |Unit|Marks|
-> |:---|:----|
-> |Unit 1|10|
-> |Unit 2|10|
-> |Unit 3|9|
-> |Unit 4|11|
-> |Unit 5|11|
-> |Unit 6|8|
-> |Forms|4|
-> |Total|63|
+|Unit|Marks|
+|:---|:----|
+|Unit 1|10|
+|Unit 2|10|
+|Unit 3|9|
+|Unit 4|11|
+|Unit 5|11|
+|Unit 6|8|
+|Forms|4|
+|Total|63|
-> |Section|Marks|
-> |:------|:----|
-> |Knowledge|21|
-> |Application|23|
-> |Thinking|12|
-> |Communication|3|
-> |Forms|4|
+|Section|Marks|
+ |:------|:----|
+ |Knowledge|21|
+ |Application|23|
+ |Thinking|12|
+ |Communication|3|
+ |Forms|4|
-> |Part|Question|
-> |:---|:-------|
-> |A|9 multiple choice|
-> |B|10 Short Answer -->
- 7 Knowledge questions
- 3 Application Questions|
-> |C|10 Open Response -->
- 10 Knowledge Questions
- 5 Application Questions
- 3 Thinking Questions
- 1 Communication Question|
+ |Part|Question|
+ |:---|:-------|
+ |A|9 multiple choice|
+ |B|10 Short Answer -->
- 7 Knowledge questions
- 3 Application Questions|
+ |C|10 Open Response -->
- 10 Knowledge Questions
- 5 Application Questions
- 3 Thinking Questions
- 1 Communication Question|
-# Essential Skills (1)
-> ## Simple Arithmetics
->> ### Addition / Subtraction
->>> | Expression | Equivalent|
->>> |:----------:|:---------:|
->>> | a + b | a + b |
->>> | (-a) + b | b - a |
->>> | a + (-b) | a - b |
->>> | (-a) + (-b) | -(a + b) |
->>> | a - b | a - b|
->>> | a - (-b) | a + b |
->>> | (-a) -(-b) | (-a) + b|
+# Unit 1: Essential Skills
->> ### Multiplication / Division
->>> | Signs | Outcome |
->>> |:-----:|:-------:|
->>> | a * b | Positive |
->>> | (-a) * b | Negative |
->>> | a * (-b) | Negative |
->>> | (-a) * (-b) | Positive |
-
->> ### BEDMAS / PEMDAS
->>> Follow ```BEDMAS``` for order of operations if there are more than one operation
-
->>> | Letter | Meaning |
->>> |:------:|:-------:|
->>> | B / P | Bracket / Parentheses |
->>> | E | Exponent |
->>> | D | Divison |
->>> | M | Multiplication |
->>> | A | Addition |
->>> | S | Subtraction |
-
->>>  -
-> ## Interval Notation
->> A notation that represents an interval as a pair of numbers.
->> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
->> ```|``` means ```such that```
->> ```E``` or ∈ means ```element of```
->> ```N``` represents **Natural Numbers** (N = {x | x > 0, x ∈ Z})
->> ```W``` represents **Whole Numbers** (W = {x | x ≥ 0, x ∈ Z})
->> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
->> ```Q``` represents **Rational Numbers** (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
-
->> | Symbol | Meaning |
->> |:------:|:-------:|
->> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
->> | [a, b] | Inclusive |
->> | a ∪ b | Union (or) |
->> | a ∩ b | Intersection (and) |
-
-> ## Pythgorean Theorem
->> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
->> a2 + b2 = c2
-
->>
-
-> ## Interval Notation
->> A notation that represents an interval as a pair of numbers.
->> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
->> ```|``` means ```such that```
->> ```E``` or ∈ means ```element of```
->> ```N``` represents **Natural Numbers** (N = {x | x > 0, x ∈ Z})
->> ```W``` represents **Whole Numbers** (W = {x | x ≥ 0, x ∈ Z})
->> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
->> ```Q``` represents **Rational Numbers** (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
-
->> | Symbol | Meaning |
->> |:------:|:-------:|
->> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
->> | [a, b] | Inclusive |
->> | a ∪ b | Union (or) |
->> | a ∩ b | Intersection (and) |
-
-> ## Pythgorean Theorem
->> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
->> a2 + b2 = c2
-
->>  +## Simple Arithmetics
-> ## Operations with Rationals
->> Q = {
+## Simple Arithmetics
-> ## Operations with Rationals
->> Q = {  | a, b ∈ Z, b ≠ 0 }
->>
->> Any operations with rationals, there are 2 sets of rules
->>> 1. ```Rules for operations with integers```
->>> 2. ```Rules for operations with fractions```
+### Addition / Subtraction
+ | Expression | Equivalent|
+ |:----------:|:---------:|
+ | a + b | a + b |
+ | (-a) + b | b - a |
+ | a + (-b) | a - b |
+ | (-a) + (-b) | -(a + b) |
+ | a - b | a - b|
+ | a - (-b) | a + b |
+ | (-a) -(-b) | (-a) + b|
->> To Add / subtract rationals, find common denominator and then add / subtract numerator
->> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
->> To Divide rationals, multiply them by the reciprocal
+### Multiplication / Division
+ | Signs | Outcome |
+ |:-----:|:-------:|
+ | a * b | Positive |
+ | (-a) * b | Negative |
+ | a * (-b) | Negative |
+ | (-a) * (-b) | Positive |
->> ### Example Simplify Fully:
->>>
| a, b ∈ Z, b ≠ 0 }
->>
->> Any operations with rationals, there are 2 sets of rules
->>> 1. ```Rules for operations with integers```
->>> 2. ```Rules for operations with fractions```
+### Addition / Subtraction
+ | Expression | Equivalent|
+ |:----------:|:---------:|
+ | a + b | a + b |
+ | (-a) + b | b - a |
+ | a + (-b) | a - b |
+ | (-a) + (-b) | -(a + b) |
+ | a - b | a - b|
+ | a - (-b) | a + b |
+ | (-a) -(-b) | (-a) + b|
->> To Add / subtract rationals, find common denominator and then add / subtract numerator
->> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
->> To Divide rationals, multiply them by the reciprocal
+### Multiplication / Division
+ | Signs | Outcome |
+ |:-----:|:-------:|
+ | a * b | Positive |
+ | (-a) * b | Negative |
+ | a * (-b) | Negative |
+ | (-a) * (-b) | Positive |
->> ### Example Simplify Fully:
->>>  [Reduce to lowest terms]
+### BEDMAS / PEMDAS
+- Follow ```BEDMAS``` for order of operations if there are more than one operation
->>>
[Reduce to lowest terms]
+### BEDMAS / PEMDAS
+- Follow ```BEDMAS``` for order of operations if there are more than one operation
->>>  [Multiply by reciprocal]
+ | Letter | Meaning |
+ |:------:|:-------:|
+ | B / P | Bracket / Parentheses |
+ | E | Exponent |
+ | D | Divison |
+ | M | Multiplication |
+ | A | Addition |
+ | S | Subtraction |
->>>
[Multiply by reciprocal]
+ | Letter | Meaning |
+ |:------:|:-------:|
+ | B / P | Bracket / Parentheses |
+ | E | Exponent |
+ | D | Divison |
+ | M | Multiplication |
+ | A | Addition |
+ | S | Subtraction |
->>> +-
+-  ->>>
->>>  [Leave as an improper fraction]
+## Interval Notation
+- A notation that represents an interval as a pair of numbers.
+- The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
+- ```|``` means ```such that```
+- ```E``` or ∈ means ```element of```
+- ```N``` represents **Natural Numbers** (N = {x | x > 0, x ∈ Z})
+- ```W``` represents **Whole Numbers** (W = {x | x ≥ 0, x ∈ Z})
+- ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
+- ```Q``` represents **Rational Numbers** (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
->> ### Shortcut for multiplying fractions
->>> cross divide to keep your numbers small
->>> Example:
->>>
[Leave as an improper fraction]
+## Interval Notation
+- A notation that represents an interval as a pair of numbers.
+- The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
+- ```|``` means ```such that```
+- ```E``` or ∈ means ```element of```
+- ```N``` represents **Natural Numbers** (N = {x | x > 0, x ∈ Z})
+- ```W``` represents **Whole Numbers** (W = {x | x ≥ 0, x ∈ Z})
+- ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
+- ```Q``` represents **Rational Numbers** (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
->> ### Shortcut for multiplying fractions
->>> cross divide to keep your numbers small
->>> Example:
->>>  ->>>
->>>  ->>>
->>>  + | Symbol | Meaning |
+ |:------:|:-------:|
+ | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
+ | [a, b] | Inclusive |
+ | a ∪ b | Union (or) |
+ | a ∩ b | Intersection (and) |
->> ## Exponent Laws
+## Pythgorean Theorem
+- a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
+- a2 + b2 = c2
->>> | Rule | Description| Example |
->>> |:----:|:----------:|:-------:|
->>> |Product|am × an = an+m|23 × 22 = 25|
->>> |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
->>> |Power of a Power|(am)n = amn|(23)2 = 26|
->>> |Power of a Quotient|
+ | Symbol | Meaning |
+ |:------:|:-------:|
+ | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
+ | [a, b] | Inclusive |
+ | a ∪ b | Union (or) |
+ | a ∩ b | Intersection (and) |
->> ## Exponent Laws
+## Pythgorean Theorem
+- a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
+- a2 + b2 = c2
->>> | Rule | Description| Example |
->>> |:----:|:----------:|:-------:|
->>> |Product|am × an = an+m|23 × 22 = 25|
->>> |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
->>> |Power of a Power|(am)n = amn|(23)2 = 26|
->>> |Power of a Quotient| =
=  |
| =
=  |
->>> |Zero as Exponents|a0 = 1|210 = 1|
->>> |Negative Exponents|a-m =
|
->>> |Zero as Exponents|a0 = 1|210 = 1|
->>> |Negative Exponents|a-m =  |1-10 =
|1-10 =  |
->>> |Rational Exponents|an/m =
|
->>> |Rational Exponents|an/m =  |
| =
=  |
+-
|
+-  +
+## Operations with Rationals
+- Q = {
+
+## Operations with Rationals
+- Q = {  | a, b ∈ Z, b ≠ 0 }
+
+- Any operations with rationals, there are 2 sets of rules
+ 1. ```Rules for operations with integers```
+ 2. ```Rules for operations with fractions```
->>> **Note:**
->>> Exponential Form --> Expanded Form
->>> 64 = 6 × 6 × 6 × 6
+- To Add / subtract rationals, find common denominator and then add / subtract numerator
+- To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
+- To Divide rationals, multiply them by the reciprocal
->> ## Scientific Notation
->>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
->>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
->>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
->>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
->>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+### Example Simplify Fully:
+-
| a, b ∈ Z, b ≠ 0 }
+
+- Any operations with rationals, there are 2 sets of rules
+ 1. ```Rules for operations with integers```
+ 2. ```Rules for operations with fractions```
->>> **Note:**
->>> Exponential Form --> Expanded Form
->>> 64 = 6 × 6 × 6 × 6
+- To Add / subtract rationals, find common denominator and then add / subtract numerator
+- To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
+- To Divide rationals, multiply them by the reciprocal
->> ## Scientific Notation
->>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
->>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
->>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
->>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
->>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+### Example Simplify Fully:
+-  [Reduce to lowest terms]
->>>
[Reduce to lowest terms]
->>>  +-
+-  [Multiply by reciprocal]
->>> **Remember**: For scientific notation, round to ```3 significant``` digits
+-
[Multiply by reciprocal]
->>> **Remember**: For scientific notation, round to ```3 significant``` digits
+-  ->> ## Rates, Ratio and Percent
->>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
->>> Examples: ```a:b, a:b:c, a/b, a to b ```
+-
->> ## Rates, Ratio and Percent
->>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
->>> Examples: ```a:b, a:b:c, a/b, a to b ```
+-  [Leave as an improper fraction]
->>> ```Rates```: A comparison of quantities expressed in different units.
->>> Example: ```10km/hour```
+### Shortcut for multiplying fractions
+- cross divide to keep your numbers small
+- Example:
+-
[Leave as an improper fraction]
->>> ```Rates```: A comparison of quantities expressed in different units.
->>> Example: ```10km/hour```
+### Shortcut for multiplying fractions
+- cross divide to keep your numbers small
+- Example:
+-  +-
+-  +-
+-  ->>> ```Percent```: A fraction or ratio in which the denominator is 100
->>> Examples: ```50%, 240/100```
+## Exponent Laws
-> ## Number Lines
->> a line that goes from a point to another point, a way to visualize set notations and the like
->>
->>> ```Percent```: A fraction or ratio in which the denominator is 100
->>> Examples: ```50%, 240/100```
+## Exponent Laws
-> ## Number Lines
->> a line that goes from a point to another point, a way to visualize set notations and the like
->>  ->> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+ | Rule | Description| Example |
+ |:----:|:----------:|:-------:|
+ |Product|am × an = an+m|23 × 22 = 25|
+ |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
+ |Power of a Power|(am)n = amn|(23)2 = 26|
+ |Power of a Quotient|
->> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+ | Rule | Description| Example |
+ |:----:|:----------:|:-------:|
+ |Product|am × an = an+m|23 × 22 = 25|
+ |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
+ |Power of a Power|(am)n = amn|(23)2 = 26|
+ |Power of a Quotient| =
=  |
| =
=  |
+ |Zero as Exponents|a0 = 1|210 = 1|
+ |Negative Exponents|a-m =
|
+ |Zero as Exponents|a0 = 1|210 = 1|
+ |Negative Exponents|a-m =  |1-10 =
|1-10 =  |
+ |Rational Exponents|an/m =
|
+ |Rational Exponents|an/m =  |
| =
=  |
+
+**Note:**
+- Exponential Form --> Expanded Form
+- 64 = 6 × 6 × 6 × 6
+
+## Scientific Notation
+- They convey accuracy and precision. It can either be written as its original number or in scientific notation:
+- 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
+- In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
+- Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
+- When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+
+-
|
+
+**Note:**
+- Exponential Form --> Expanded Form
+- 64 = 6 × 6 × 6 × 6
+
+## Scientific Notation
+- They convey accuracy and precision. It can either be written as its original number or in scientific notation:
+- 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
+- In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
+- Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
+- When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+
+-  +
+- **Remember**: For scientific notation, round to ```3 significant``` digits
+
+## Rates, Ratio and Percent
+- ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+- Examples: ```a:b, a:b:c, a/b, a to b ```
+
+- ```Rates```: A comparison of quantities expressed in different units.
+- Example: ```10km/hour```
+
+- ```Percent```: A fraction or ratio in which the denominator is 100
+- Examples: ```50%, 240/100```
+
+## Number Lines
+- a line that goes from a point to another point, a way to visualize set notations and the like
+-
+
+- **Remember**: For scientific notation, round to ```3 significant``` digits
+
+## Rates, Ratio and Percent
+- ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+- Examples: ```a:b, a:b:c, a/b, a to b ```
+
+- ```Rates```: A comparison of quantities expressed in different units.
+- Example: ```10km/hour```
+
+- ```Percent```: A fraction or ratio in which the denominator is 100
+- Examples: ```50%, 240/100```
+
+## Number Lines
+- a line that goes from a point to another point, a way to visualize set notations and the like
+-  +- A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
-> ## Tips
->> Watch out for the ```+/-``` signs
->> Make sure to review your knowledge of the exponent laws
->> For scientific notation, watch out for the decimal point
->> Use shortcut when multiplying fractions
+## Tips
+- Watch out for the ```+/-``` signs
+- Make sure to review your knowledge of the exponent laws
+- For scientific notation, watch out for the decimal point
+- Use shortcut when multiplying fractions
-# Polyomials (2)
-> ## Introduction to Polynomials
->> A ```variable``` is a letter that represents one or more numbers
->> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
->> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
-> ## Methods to solve a polynomial
->> 1. ```Combine like terms```
->> 2. ```Dividing polynomials```
->> 3. ```Multiplying polynomials```
+# Unit 2: Polyomials
+## Introduction to Polynomials
+- A ```variable``` is a letter that represents one or more numbers
+- An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
+- When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+## Methods to solve a polynomial
+ 1. ```Combine like terms```
+ 2. ```Dividing polynomials```
+ 3. ```Multiplying polynomials```
-> ## Simplifying Alegebraic Expressions
->> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+## Simplifying Alegebraic Expressions
+- An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
-> ## Factoring
->>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
->> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
->> (e.g 5x + 10 = 5(x + 2) ).
+## Factoring
+- Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+- equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+- (e.g 5x + 10 = 5(x + 2) ).
->> |Type of Polynomial|Definition|
->> |:-----------------|:---------|
->> |Monomial|Polynomial that only has one term|
->> |Binomial|Polynomial that only has 2 terms|
->> |Trinomial|polynomial that only has 3 terms|
+|Type of Polynomial|Definition|
+ |:-----------------|:---------|
+ |Monomial|Polynomial that only has one term|
+ |Binomial|Polynomial that only has 2 terms|
+ |Trinomial|polynomial that only has 3 terms|
->> |Type|Example|
->> |:--:|:-----:|
->> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
->> |Difference with Squares|a2-b2 = (a+b)(a-b)|
->> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
->> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
->> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
->> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+ |Type|Example|
+ |:--:|:-----:|
+ |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+ |Difference with Squares|a2-b2 = (a+b)(a-b)|
+ |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+ |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+ |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+ |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
-> ## Shortcuts
+## Shortcuts
->>
+- A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
-> ## Tips
->> Watch out for the ```+/-``` signs
->> Make sure to review your knowledge of the exponent laws
->> For scientific notation, watch out for the decimal point
->> Use shortcut when multiplying fractions
+## Tips
+- Watch out for the ```+/-``` signs
+- Make sure to review your knowledge of the exponent laws
+- For scientific notation, watch out for the decimal point
+- Use shortcut when multiplying fractions
-# Polyomials (2)
-> ## Introduction to Polynomials
->> A ```variable``` is a letter that represents one or more numbers
->> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
->> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
-> ## Methods to solve a polynomial
->> 1. ```Combine like terms```
->> 2. ```Dividing polynomials```
->> 3. ```Multiplying polynomials```
+# Unit 2: Polyomials
+## Introduction to Polynomials
+- A ```variable``` is a letter that represents one or more numbers
+- An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
+- When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+## Methods to solve a polynomial
+ 1. ```Combine like terms```
+ 2. ```Dividing polynomials```
+ 3. ```Multiplying polynomials```
-> ## Simplifying Alegebraic Expressions
->> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+## Simplifying Alegebraic Expressions
+- An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
-> ## Factoring
->>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
->> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
->> (e.g 5x + 10 = 5(x + 2) ).
+## Factoring
+- Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+- equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+- (e.g 5x + 10 = 5(x + 2) ).
->> |Type of Polynomial|Definition|
->> |:-----------------|:---------|
->> |Monomial|Polynomial that only has one term|
->> |Binomial|Polynomial that only has 2 terms|
->> |Trinomial|polynomial that only has 3 terms|
+|Type of Polynomial|Definition|
+ |:-----------------|:---------|
+ |Monomial|Polynomial that only has one term|
+ |Binomial|Polynomial that only has 2 terms|
+ |Trinomial|polynomial that only has 3 terms|
->> |Type|Example|
->> |:--:|:-----:|
->> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
->> |Difference with Squares|a2-b2 = (a+b)(a-b)|
->> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
->> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
->> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
->> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+ |Type|Example|
+ |:--:|:-----:|
+ |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+ |Difference with Squares|a2-b2 = (a+b)(a-b)|
+ |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+ |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+ |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+ |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
-> ## Shortcuts
+## Shortcuts
->>  +-
+-  -> ## Foil / Rainbow Method
->>
-> ## Foil / Rainbow Method
->> 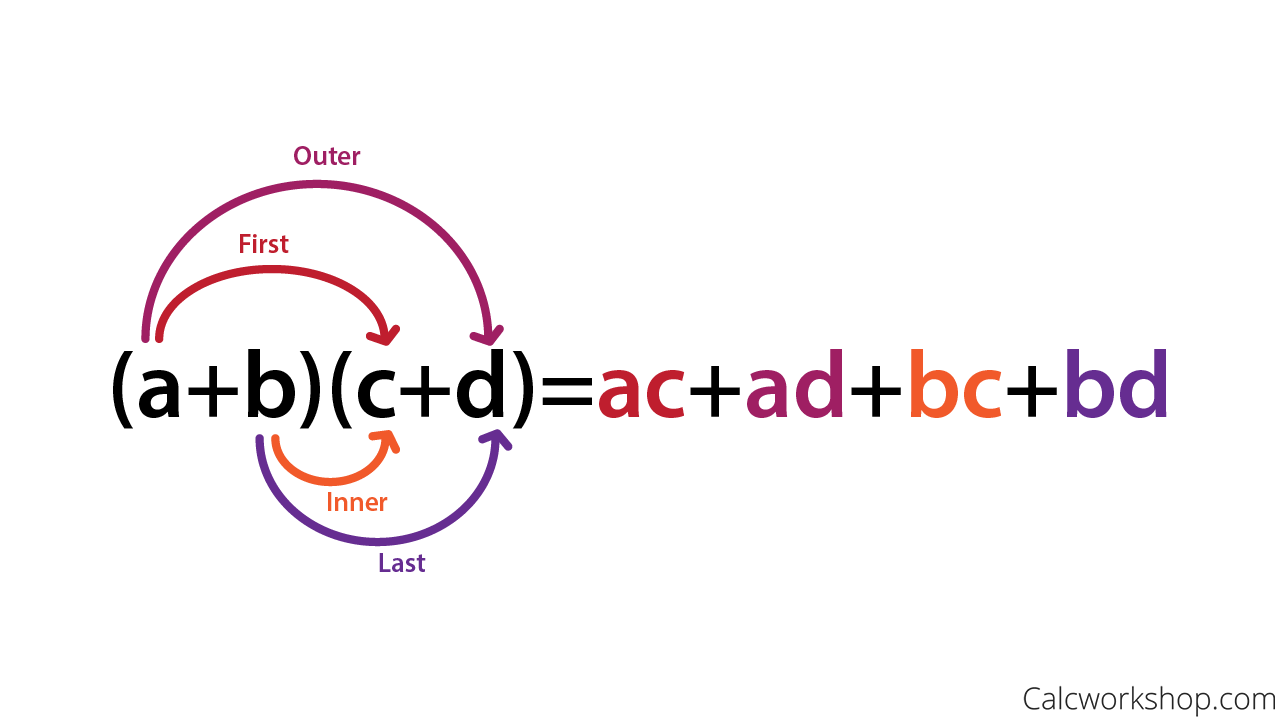 +## Foil / Rainbow Method
+-
+## Foil / Rainbow Method
+-  -> ## Definitions
->> ```Term``` a variable that may have coefficient(s) or a constant
->> ```Alebraic Expressions```: made up of one or more terms
->> ```Like-terms```: same variables raised to the same exponent
+## Definitions
+- ```Term``` a variable that may have coefficient(s) or a constant
+- ```Alebraic Expressions```: made up of one or more terms
+- ```Like-terms```: same variables raised to the same exponent
-> ## Tips
->> Be sure to factor fully
->> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
->> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
->> Remember your formulas
->> Simplify first, combine like terms
+## Tips
+- Be sure to factor fully
+- Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+- Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+- Remember your formulas
+- Simplify first, combine like terms
-# Solving Equations and Inequailties (3)
-> ## Equations
->> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
->> To ```solve``` and equation is to find the variable that makes the statement true
->> ### Methods to solve an equation
->>> 1. Expand and simplify both sides
->>> 2. Isolate using reverse order of operations
->>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+# Unit 3: Solving Equations and Inequailties
+
+## Equations
+- a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+- To ```solve``` and equation is to find the variable that makes the statement true
+### Methods to solve an equation
+ 1. Expand and simplify both sides
+ 2. Isolate using reverse order of operations
+ 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
->
-> ## Absolute Values
->> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->> equations will have the absolute bracket be positive while the other negative.
->> Absolute values are written in the form ```| x |```
->> where
->> if x > 0, | x | = x
->> if x = 0, | x | = 0
->> if x < 0, | x | = -x
+## Absolute Values
+- There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+- equations will have the absolute bracket be positive while the other negative.
+- Absolute values are written in the form ```| x |```
+- where
+ - if x > 0, | x | = x
+ - if x = 0, | x | = 0
+ - if x < 0, | x | = -x
-> ## Quadractic Equations
->> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
->> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
->> Solve quadratic equation by:
->> 1. Isolation
->> a(x+b)2 + k = 0
->> 2. Factor using zero-product property
->> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
->> (x-a)(x-b)=0
->> x = a, b
+## Quadractic Equations
+- ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+- ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+- Solve quadratic equation by:
->>
-> ## Definitions
->> ```Term``` a variable that may have coefficient(s) or a constant
->> ```Alebraic Expressions```: made up of one or more terms
->> ```Like-terms```: same variables raised to the same exponent
+## Definitions
+- ```Term``` a variable that may have coefficient(s) or a constant
+- ```Alebraic Expressions```: made up of one or more terms
+- ```Like-terms```: same variables raised to the same exponent
-> ## Tips
->> Be sure to factor fully
->> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
->> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
->> Remember your formulas
->> Simplify first, combine like terms
+## Tips
+- Be sure to factor fully
+- Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+- Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+- Remember your formulas
+- Simplify first, combine like terms
-# Solving Equations and Inequailties (3)
-> ## Equations
->> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
->> To ```solve``` and equation is to find the variable that makes the statement true
->> ### Methods to solve an equation
->>> 1. Expand and simplify both sides
->>> 2. Isolate using reverse order of operations
->>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+# Unit 3: Solving Equations and Inequailties
+
+## Equations
+- a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+- To ```solve``` and equation is to find the variable that makes the statement true
+### Methods to solve an equation
+ 1. Expand and simplify both sides
+ 2. Isolate using reverse order of operations
+ 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
->
-> ## Absolute Values
->> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->> equations will have the absolute bracket be positive while the other negative.
->> Absolute values are written in the form ```| x |```
->> where
->> if x > 0, | x | = x
->> if x = 0, | x | = 0
->> if x < 0, | x | = -x
+## Absolute Values
+- There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+- equations will have the absolute bracket be positive while the other negative.
+- Absolute values are written in the form ```| x |```
+- where
+ - if x > 0, | x | = x
+ - if x = 0, | x | = 0
+ - if x < 0, | x | = -x
-> ## Quadractic Equations
->> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
->> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
->> Solve quadratic equation by:
->> 1. Isolation
->> a(x+b)2 + k = 0
->> 2. Factor using zero-product property
->> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
->> (x-a)(x-b)=0
->> x = a, b
+## Quadractic Equations
+- ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+- ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+- Solve quadratic equation by:
->>  + 1. Isolation
+ - a(x+b)2 + k = 0
+ 2. Factor using zero-product property
+ - ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+ - (x-a)(x-b)=0
+ - x = a, b
->> Note:
->> √x2 = ± x (There are 2 possible solutions)
->> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+-
+ 1. Isolation
+ - a(x+b)2 + k = 0
+ 2. Factor using zero-product property
+ - ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+ - (x-a)(x-b)=0
+ - x = a, b
->> Note:
->> √x2 = ± x (There are 2 possible solutions)
->> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+-  +
+**Note:**
+- √x2 = ± x (There are 2 possible solutions)
+- ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
-> ## Tips
->> ```Absolute Values``` can have 2 solutions
->> ```Quadratics``` can also have 2 solutions
->> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
+## Tips
+- ```Absolute Values``` can have 2 solutions
+- ```Quadratics``` can also have 2 solutions
+- Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
-# Measurement and Geometry (4)
-> ## Angle Theorems
-> 1. ```Transversal Parallel Line Theorems``` (TPT)
-> a. Alternate Angles are Equal ```(Z-Pattern)```
-> b. Corresponding Angles Equal ```(F-Pattern)```
-> c. Interior Angles add up to 180 ```(C-Pattern)```
+# Unit 4: Measurement and Geometry
+## Angle Theorems
+
+1. ```Transversal Parallel Line Theorems``` (TPT)
+ a. Alternate Angles are Equal ```(Z-Pattern)```
+ b. Corresponding Angles Equal ```(F-Pattern)```
+ c. Interior Angles add up to 180 ```(C-Pattern)```
>
+
+**Note:**
+- √x2 = ± x (There are 2 possible solutions)
+- ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
-> ## Tips
->> ```Absolute Values``` can have 2 solutions
->> ```Quadratics``` can also have 2 solutions
->> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
+## Tips
+- ```Absolute Values``` can have 2 solutions
+- ```Quadratics``` can also have 2 solutions
+- Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
-# Measurement and Geometry (4)
-> ## Angle Theorems
-> 1. ```Transversal Parallel Line Theorems``` (TPT)
-> a. Alternate Angles are Equal ```(Z-Pattern)```
-> b. Corresponding Angles Equal ```(F-Pattern)```
-> c. Interior Angles add up to 180 ```(C-Pattern)```
+# Unit 4: Measurement and Geometry
+## Angle Theorems
+
+1. ```Transversal Parallel Line Theorems``` (TPT)
+ a. Alternate Angles are Equal ```(Z-Pattern)```
+ b. Corresponding Angles Equal ```(F-Pattern)```
+ c. Interior Angles add up to 180 ```(C-Pattern)```
> 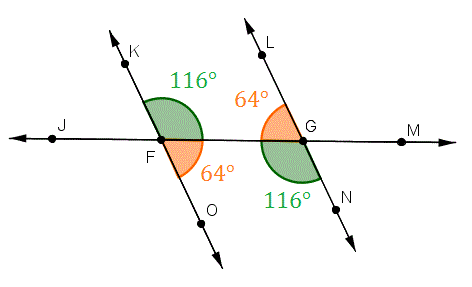 -> 2. ```Supplementary Angle Triangle``` (SAT)
-> - When two angles add up to 180 degrees
+2. ```Supplementary Angle Triangle``` (SAT)
+ - When two angles add up to 180 degrees
->
-> 2. ```Supplementary Angle Triangle``` (SAT)
-> - When two angles add up to 180 degrees
+2. ```Supplementary Angle Triangle``` (SAT)
+ - When two angles add up to 180 degrees
->  + -
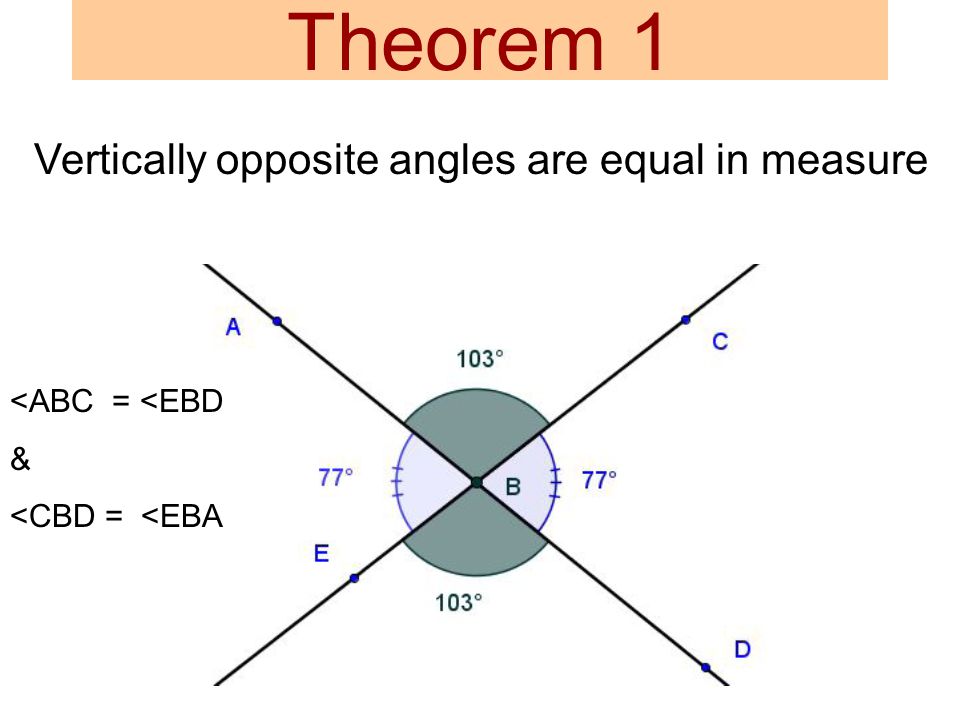
+ -  -> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
-> - Two lines intersect, two angles form opposite. They have equal measures
+3. ```Opposite Angle Theorem (OAT)``` (OAT)
+ - Two lines intersect, two angles form opposite. They have equal measures
->
-> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
-> - Two lines intersect, two angles form opposite. They have equal measures
+3. ```Opposite Angle Theorem (OAT)``` (OAT)
+ - Two lines intersect, two angles form opposite. They have equal measures
->  + -
+ -  -> 4. ```Complementary Angle Theorem``` (CAT)
-> - The sum of two angles that add up to 90 degrees
+4. ```Complementary Angle Theorem``` (CAT)
+ - The sum of two angles that add up to 90 degrees
->
-> 4. ```Complementary Angle Theorem``` (CAT)
-> - The sum of two angles that add up to 90 degrees
+4. ```Complementary Angle Theorem``` (CAT)
+ - The sum of two angles that add up to 90 degrees
->  + -
+ -  -> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
-> - The sum of the three interior angles of any triangle is 180 degrees
+5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+ - The sum of the three interior angles of any triangle is 180 degrees
->
-> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
-> - The sum of the three interior angles of any triangle is 180 degrees
+5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+ - The sum of the three interior angles of any triangle is 180 degrees
->  + -
+ -  -> 6. ```Exterior Angle Theorem``` (EAT)
-> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+6. ```Exterior Angle Theorem``` (EAT)
+ - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
->
-> 6. ```Exterior Angle Theorem``` (EAT)
-> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+6. ```Exterior Angle Theorem``` (EAT)
+ - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
->  + -
+ - -> 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+7. ``` Isosceles Triangle Theorem``` (ITT)
+ - The base angles in any isosceles triangle are equal
->
-> 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+7. ``` Isosceles Triangle Theorem``` (ITT)
+ - The base angles in any isosceles triangle are equal
->  + -
+ -  -> 8. ```Sum of The Interior Angle of a Polygon```
-> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+8. ```Sum of The Interior Angle of a Polygon```
+ - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
->
-> 8. ```Sum of The Interior Angle of a Polygon```
-> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+8. ```Sum of The Interior Angle of a Polygon```
+ - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
->  + -
+ -  -> 9. ```Exterior Angles of a Convex Polygon```
-> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+9. ```Exterior Angles of a Convex Polygon```
+ - The sum of the exterior angle of any convex polygon is always ```360 degrees```
->
-> 9. ```Exterior Angles of a Convex Polygon```
-> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+9. ```Exterior Angles of a Convex Polygon```
+ - The sum of the exterior angle of any convex polygon is always ```360 degrees```
->  + -
+ -  -> ## Properties of Quadrilaterals
->> Determine the shape using the properties of it
+## Properties of Quadrilaterals
+- Determine the shape using the properties of it
->> |Figure|Properties|
->> |:-----|:---------|
->> |Scalene Triangle|no sides equal|Length of line segment|
->> |Isosceles Triangle| two sides equal|Length of line segment|
->> |Equilateral Triangle|All sides equal|Length of line segment|
->> |Right Angle Triangle|Two sides are perpendicular to each other|
->> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
->> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
->> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
->> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
->> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
->> |Kite|The diagonals are perpendicular|
-
-> ## 2D Geometry Equations
->> |Shape|Formula|Picture|
->> |:----|:------|:------|
->> |Rectangle|```Area```: lw
-> ## Properties of Quadrilaterals
->> Determine the shape using the properties of it
+## Properties of Quadrilaterals
+- Determine the shape using the properties of it
->> |Figure|Properties|
->> |:-----|:---------|
->> |Scalene Triangle|no sides equal|Length of line segment|
->> |Isosceles Triangle| two sides equal|Length of line segment|
->> |Equilateral Triangle|All sides equal|Length of line segment|
->> |Right Angle Triangle|Two sides are perpendicular to each other|
->> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
->> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
->> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
->> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
->> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
->> |Kite|The diagonals are perpendicular|
-
-> ## 2D Geometry Equations
->> |Shape|Formula|Picture|
->> |:----|:------|:------|
->> |Rectangle|```Area```: lw
```Perimeter```: 2(l+w)| |
->> |Triangle|```Area```: bh/2
|
->> |Triangle|```Area```: bh/2
```Perimeter```: a+b+c| |
->> |Circle|```Area```: πr2
|
->> |Circle|```Area```: πr2
```Circumference```: 2πr or πd| |
->> |Trapezoid|```Area```: (a+b)h/2
|
->> |Trapezoid|```Area```: (a+b)h/2
```Perimeter```: a+b+c+d| |
-
-> ## 3D Geometry Equations
->> |3D Object|Formula|Picture|
->> |:----|:------|:------|
->> |Rectangular Prism|```Volume```: lwh
|
-
-> ## 3D Geometry Equations
->> |3D Object|Formula|Picture|
->> |:----|:------|:------|
->> |Rectangular Prism|```Volume```: lwh
```SA```: 2(lw+lh+wh)| |
->> |Square Based Pyramid|```Volume```: 1⁄3b2h
|
->> |Square Based Pyramid|```Volume```: 1⁄3b2h
```SA```: 2bs+b2| |
->> |Sphere|```Volume```: 4⁄3πr3
|
->> |Sphere|```Volume```: 4⁄3πr3
```SA```: 4πr2| |
->> |Cone|```Volume```: 1⁄3πr2h
|
->> |Cone|```Volume```: 1⁄3πr2h
```SA```: πrs+πr2| |
->> |Cylinder|```Volume```: πr2h
|
->> |Cylinder|```Volume```: πr2h
```SA```: 2πr2+2πh| |
->> |Triangular Prism|```Volume```: ah+bh+ch+bl
|
->> |Triangular Prism|```Volume```: ah+bh+ch+bl
```SA```: 1⁄2blh| |
-
-
-> ## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
->> ### 2D Objects
-
->> |Shape|Maximum Area|Minimum Perimeter|
->> |:----|:-----------|:----------------|
->> |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
|
-
-
-> ## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
->> ### 2D Objects
-
->> |Shape|Maximum Area|Minimum Perimeter|
->> |:----|:-----------|:----------------|
->> |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
A = lw
Amax = (w)(w)
Amax = w2|A rectangle must be a square to minimaze the perimeter for a given area. The length is equal to the width.
P = 2(l+w)
Pmin = 2(w)(w)
Pmin = 2(2w)
Pmin = 4w|
->> |3-sided rectangle|l = 2w
A = lw
Amax = 2w(w)
Amax = 2w2|l = 2w
P = l+w2
Pmin = 2w+2w
Pmin = 4w|
-
-
->> ### 3D Objects
-
->> |3D Object|Maximum Volumne|Minimum Surface Area|
->> |:--------|:--------------|:-------------------|
->> |Cylinder(closed-top)|The cylinder must be similar to a cube where h = 2r
V = πr2h
Vmax = πr2(2r)
Vmax = 2πr3|The cylinder must be similar to a cube where h = 2r
SA = 2πr2+2πrh
SAmin = 2πr2+2πr(2r)
SAmin = 2πr2+4πr2
SAmin = 6πr2|
->> |Rectangular Prism(closed-top)|The prism must be a cube,
where l = w = h
V = lwh
Vmax = (w)(w)(w)
Vmax = w3|The prism must be a cube,
where l = w = h
SA = 2lh+2lw+2wh
SAmin = 2w2+2w2+2w2
SAmin = 6w2|
->> |Cylinder(open-top)|h = r
V = πr2h
Vmax = πr2(r)
Vmax = πr3|h = r
SA = πr2+2πrh
SAmin = πr2+2πr(r)
SAmin = πr2+2πr2
SAmin = 3πr2|
->> |Square-Based Rectangular Prism(open-top)|h = w/2
V = lwh
Vmax = (w)(w)(w⁄2)
Vmax = w3⁄2|h = w/2
SA = w2+4wh
SAmin = w2+4w(w⁄2)
SAmin = w2+2w2
SAmin = 3w2|
-
-> ## Labelling
->> Given any polygons, labelling the vertices must always:
->> 1. use ```CAPITAL LETTERS```
->> 2. they have to be labeled in ```clockwise``` or ```counter-clockwise``` directions
->> For a triangle, the side lengths are labeled in ```LOWERCASE LETTERS``` associated to the opposite side of the vertex
-
->> 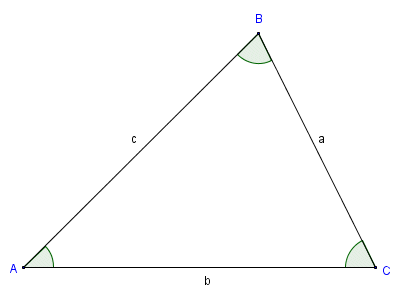 -
-> ## Median
->> Each median divides the triangle into 2 smaller triangles of equal area
->> The centroid is exactly
-
-> ## Median
->> Each median divides the triangle into 2 smaller triangles of equal area
->> The centroid is exactly  the way of each median from the vertex, or
the way of each median from the vertex, or  the way from the midpoint of the opposite side, or ```2:1``` ratio
->> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
-
->>
the way from the midpoint of the opposite side, or ```2:1``` ratio
->> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
-
->>  -
-> ## Terms:
->> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
->> ```Orthocenter```: where all 3 altitudes of the triangle intersect
->>>
-
-> ## Terms:
->> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
->> ```Orthocenter```: where all 3 altitudes of the triangle intersect
->>> 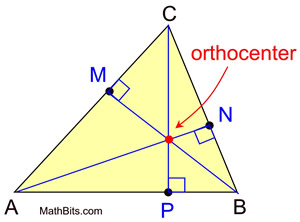 ->> ```Midpoint```: A point on a line where the length of either side of the point are equal
->> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
->> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
->> ```Centroid```: The intersection of the 3 medians of a triangle
->>>
->> ```Midpoint```: A point on a line where the length of either side of the point are equal
->> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
->> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
->> ```Centroid```: The intersection of the 3 medians of a triangle
->>>  -
-> ## Proportionality theorem:
->> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
->> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
->> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
->>
-
-> ## Proportionality theorem:
->> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
->> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
->> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
->>  -
-> ## Tips
->> Make sure to know your optimization formualas
->> Read the word problems carefully, determine which formual to use
->> Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
->> To find ```missing area```, take what you have, subtract what you don't want
->> Don't be afraid to draw lines to help you solve the problem
-
-
-# Analytical Geometry and Linear Relations (5)
-> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
-> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
-> ## Slope and Equation of Line
->> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```the rate of change```
->> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
->> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
->> ```Y-intercept Form```: **y = mx + b**
->> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
->> The slope of a vertical lines is undefined
->> The slope of a horizontal line is 0
->> Parallel lines have the ```same slope```
->> Perpendicular slopes are negative reciprocals
-
-> ## Relations
->> A relation can be described using
->> 1. Table of Values (see below)
->> 2. Equations (y = 3x + 5)
->> 3. Graphs (Graphing the equation)
->> 4. Words
->> When digging into the earth, the temperature rises according to the
->> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
->> degrees and **h** is the depth in meters.
-
-> ## Perpendicular Lines
->> To find the perpendicular slope, you will need to find the slope point
->> Formula: slope1 × slope2 = -1
->> Notation: m⊥
->>
-
-> ## Tips
->> Make sure to know your optimization formualas
->> Read the word problems carefully, determine which formual to use
->> Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
->> To find ```missing area```, take what you have, subtract what you don't want
->> Don't be afraid to draw lines to help you solve the problem
-
-
-# Analytical Geometry and Linear Relations (5)
-> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
-> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
-> ## Slope and Equation of Line
->> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```the rate of change```
->> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
->> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
->> ```Y-intercept Form```: **y = mx + b**
->> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
->> The slope of a vertical lines is undefined
->> The slope of a horizontal line is 0
->> Parallel lines have the ```same slope```
->> Perpendicular slopes are negative reciprocals
-
-> ## Relations
->> A relation can be described using
->> 1. Table of Values (see below)
->> 2. Equations (y = 3x + 5)
->> 3. Graphs (Graphing the equation)
->> 4. Words
->> When digging into the earth, the temperature rises according to the
->> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
->> degrees and **h** is the depth in meters.
-
-> ## Perpendicular Lines
->> To find the perpendicular slope, you will need to find the slope point
->> Formula: slope1 × slope2 = -1
->> Notation: m⊥
->> 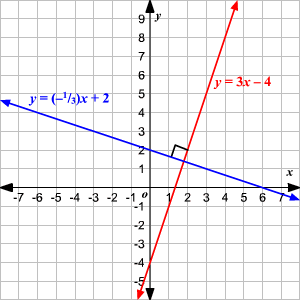 -
-
-> ## Definitions
->> ```Parallel```: 2 lines with the same slope
->> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
->> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
->> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
->> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
->> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
->> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
->> ```Collinear Points```: points that line on the same straight line
-
-> ## Variables
->> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
->> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
-
-> ## Statistics
->> ```Interpolation```: Data **inside** the given data set range.
->> ```Extrapolation```: Data **outside** the data set range.
->> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
->> and it represents the trend of a graph.
->> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
->> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
-
-> ## Time - Distance Graph
->> Time is the independent variable and distance is the dependent variable
->> You can't go backwards on the x-axis, as you can't go back in time
->> Plot the points accordingly
->> Draw the lines accordingly
->>
-
-
-> ## Definitions
->> ```Parallel```: 2 lines with the same slope
->> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
->> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
->> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
->> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
->> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
->> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
->> ```Collinear Points```: points that line on the same straight line
-
-> ## Variables
->> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
->> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
-
-> ## Statistics
->> ```Interpolation```: Data **inside** the given data set range.
->> ```Extrapolation```: Data **outside** the data set range.
->> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
->> and it represents the trend of a graph.
->> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
->> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
-
-> ## Time - Distance Graph
->> Time is the independent variable and distance is the dependent variable
->> You can't go backwards on the x-axis, as you can't go back in time
->> Plot the points accordingly
->> Draw the lines accordingly
->> 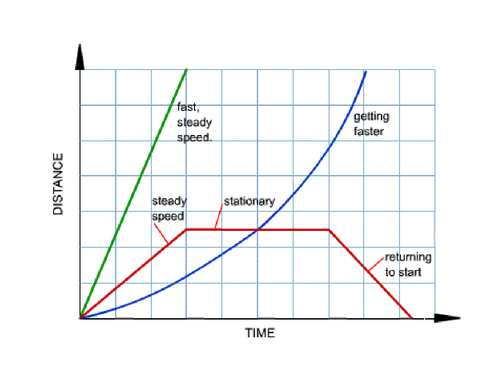 -
->> **Direction is always referring to:**
-
->> 1. ```go towards home```
->> 2. ```going away from home```
->> 3. ```stop```
-
-> ## Scatterplot and Line of Best Fit
->> A scatterplot graph is there to show the relation between two variables in a table of values.
->> A line of best fit is a straight line that describes the relation between two variables.
->> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>
-
->> **Direction is always referring to:**
-
->> 1. ```go towards home```
->> 2. ```going away from home```
->> 3. ```stop```
-
-> ## Scatterplot and Line of Best Fit
->> A scatterplot graph is there to show the relation between two variables in a table of values.
->> A line of best fit is a straight line that describes the relation between two variables.
->> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>  -
->> ### How To Determine the Equation Of a Line of Best Fit
->> 1. Find two points **```ON```** the ```line of best fit```
->> 2. Determine the ```slope``` using the two points
->> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
-
-> ## Table of values
->> To find first differences or any points on the line, you can use a ```table of values```
-
->>| y | x |First Difference|
->>|:--|:--|:---------------|
->>|-1|-2|.....|
->>|0|-1|(-1)-(-2) = 1|
->>|1|0|0 - (-1) = 1|
->>|2|1|1 - 0 = 1|
->>|3|2|2 - 1 = 1|
->>|4|3|3 - 2 = 1|
-
-> ## Tips
->> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
->> Draw your ```Line of Best Fit``` correctly
->> Read the word problems carefully, and make sure you understand it when graphing things
->> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
->> Label your lines
-
-# System of Equations (6)
-
-> ## Linear System
->> Two or more equation that you are working on all together at once on the same set of axes.
->> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
->> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
-
->> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
->> when **Profit = 0**. There is no gain or loss.
-
->> ### Number of Solutions
->>>
-
->> ### How To Determine the Equation Of a Line of Best Fit
->> 1. Find two points **```ON```** the ```line of best fit```
->> 2. Determine the ```slope``` using the two points
->> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
-
-> ## Table of values
->> To find first differences or any points on the line, you can use a ```table of values```
-
->>| y | x |First Difference|
->>|:--|:--|:---------------|
->>|-1|-2|.....|
->>|0|-1|(-1)-(-2) = 1|
->>|1|0|0 - (-1) = 1|
->>|2|1|1 - 0 = 1|
->>|3|2|2 - 1 = 1|
->>|4|3|3 - 2 = 1|
-
-> ## Tips
->> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
->> Draw your ```Line of Best Fit``` correctly
->> Read the word problems carefully, and make sure you understand it when graphing things
->> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
->> Label your lines
-
-# System of Equations (6)
-
-> ## Linear System
->> Two or more equation that you are working on all together at once on the same set of axes.
->> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
->> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
-
->> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
->> when **Profit = 0**. There is no gain or loss.
-
->> ### Number of Solutions
->>>  -
-> ## Discriminant
->> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
->> coefficients and constant of a quadratic equation: **y = ax2 + bx + c**
->> D = b2 - 4ac
->> D > 0 ```(2 distinct real solutions)```
->> D = 0 ```(1 real solution)```
->> D < 0 ```(no real solutions)```
-
->>
-
-> ## Discriminant
->> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
->> coefficients and constant of a quadratic equation: **y = ax2 + bx + c**
->> D = b2 - 4ac
->> D > 0 ```(2 distinct real solutions)```
->> D = 0 ```(1 real solution)```
->> D < 0 ```(no real solutions)```
-
->>  -
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->>
-
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->>  -
->> There are 3 possible cases
->> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
-
-
-> # Ways to solve Systems of Equations
-> 1. Subsitution
-> Here we eliminate a variable by subbing in another variable from another equation
-> We usually do this method if a variable is easily isolated
-> Example:
-> - ```
-> y = x + 10 (1)
-> x + y + 34 = 40 (2)
-> ```
-> We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
-> ```x + (x + 10) + 34 = 40```
-> ```2x + 44 = 40```
-> ```2x = -4```
-> ```x = -2```
-> Then solve for ```y```
-> ```y = -2 + 10```
-> ```y = -8```
-
-> 2. Elimination
-> Here we eliminate a variable by basically eliminate a variable from an equation
-> We usually use this method first when the variables are not easily isolated, then use subsitution to solve
-> Example:
-> - ```
-> 2x + 3y = 10 (1)
-> 4x + 3y = 14 (2)
-> ```
-> We can then use elimination
-> ```
-> 4x + 3y = 14
-> 2x + 3y = 10
-> ------------
-> 2x + 0 = 4
-> x = 2
-> ```
-> Then sub the value of ```x``` into an original equation and solve for ```y```
-> ```2(2) + 3y = 10```
-> ```3y = 6```
-> ```y = 2```
-
-> 3. Graphing
-> we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
-
-> ## Solving Systems of Linear Inequalities
->> Find the intersection region as the ```solution```.
->> ## If:
-
->> | |Use ```Dash``` line|Use ```Solid line```|
->> |:-|:------------------|:-------------------|
->> |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
->> |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
-
->> ## If
-
->> |x > a
-
->> There are 3 possible cases
->> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
-
-
-> # Ways to solve Systems of Equations
-> 1. Subsitution
-> Here we eliminate a variable by subbing in another variable from another equation
-> We usually do this method if a variable is easily isolated
-> Example:
-> - ```
-> y = x + 10 (1)
-> x + y + 34 = 40 (2)
-> ```
-> We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
-> ```x + (x + 10) + 34 = 40```
-> ```2x + 44 = 40```
-> ```2x = -4```
-> ```x = -2```
-> Then solve for ```y```
-> ```y = -2 + 10```
-> ```y = -8```
-
-> 2. Elimination
-> Here we eliminate a variable by basically eliminate a variable from an equation
-> We usually use this method first when the variables are not easily isolated, then use subsitution to solve
-> Example:
-> - ```
-> 2x + 3y = 10 (1)
-> 4x + 3y = 14 (2)
-> ```
-> We can then use elimination
-> ```
-> 4x + 3y = 14
-> 2x + 3y = 10
-> ------------
-> 2x + 0 = 4
-> x = 2
-> ```
-> Then sub the value of ```x``` into an original equation and solve for ```y```
-> ```2(2) + 3y = 10```
-> ```3y = 6```
-> ```y = 2```
-
-> 3. Graphing
-> we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
-
-> ## Solving Systems of Linear Inequalities
->> Find the intersection region as the ```solution```.
->> ## If:
-
->> | |Use ```Dash``` line|Use ```Solid line```|
->> |:-|:------------------|:-------------------|
->> |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
->> |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
-
->> ## If
-
->> |x > a
x ≥ a|
->> |:------------------|
->> shade the region on the **right**
-
->> ## If
-
->> |x < a
x ≤ a|
->> |:------------------|
->> shade the region on the **left**
-
->> Step 1. change all inequalities to ```y-intercept form```
->> Step 2. graph the line
->> Step 3. shade the region where all the regions overlap
-
->> 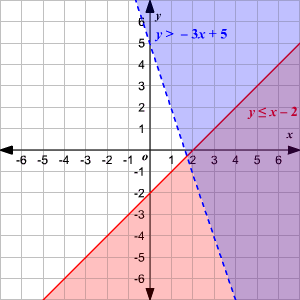 -
-
-> ## Tips
->> Read the questions carefully and model the system of equations correctly
->> Be sure to name your equations
->> Label your lines
+ |Figure|Properties|
+ |:-----|:---------|
+ |Scalene Triangle|no sides equal|Length of line segment|
+ |Isosceles Triangle| two sides equal|Length of line segment|
+ |Equilateral Triangle|All sides equal|Length of line segment|
+ |Right Angle Triangle|Two sides are perpendicular to each other|
+ |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+ |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+ |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+ |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+ |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+ |Kite|The diagonals are perpendicular|
+
+## 2D Geometry Equations
+ |Shape|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangle|```Area```: lw
-
-
-> ## Tips
->> Read the questions carefully and model the system of equations correctly
->> Be sure to name your equations
->> Label your lines
+ |Figure|Properties|
+ |:-----|:---------|
+ |Scalene Triangle|no sides equal|Length of line segment|
+ |Isosceles Triangle| two sides equal|Length of line segment|
+ |Equilateral Triangle|All sides equal|Length of line segment|
+ |Right Angle Triangle|Two sides are perpendicular to each other|
+ |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+ |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+ |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+ |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+ |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+ |Kite|The diagonals are perpendicular|
+
+## 2D Geometry Equations
+ |Shape|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangle|```Area```: lw
```Perimeter```: 2(l+w)| |
+ |Triangle|```Area```: bh/2
|
+ |Triangle|```Area```: bh/2
```Perimeter```: a+b+c| |
+ |Circle|```Area```: πr2
|
+ |Circle|```Area```: πr2
```Circumference```: 2πr or πd| |
+ |Trapezoid|```Area```: (a+b)h/2
|
+ |Trapezoid|```Area```: (a+b)h/2
```Perimeter```: a+b+c+d| |
+
+## 3D Geometry Equations
+|3D Object|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangular Prism|```Volume```: lwh
|
+
+## 3D Geometry Equations
+|3D Object|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangular Prism|```Volume```: lwh
```SA```: 2(lw+lh+wh)| |
+ |Square Based Pyramid|```Volume```: 1⁄3b2h
|
+ |Square Based Pyramid|```Volume```: 1⁄3b2h
```SA```: 2bs+b2| |
+ |Sphere|```Volume```: 4⁄3πr3
|
+ |Sphere|```Volume```: 4⁄3πr3
```SA```: 4πr2| |
+ |Cone|```Volume```: 1⁄3πr2h
|
+ |Cone|```Volume```: 1⁄3πr2h
```SA```: πrs+πr2| |
+ |Cylinder|```Volume```: πr2h
|
+ |Cylinder|```Volume```: πr2h
```SA```: 2πr2+2πh| |
+ |Triangular Prism|```Volume```: ah+bh+ch+bl
|
+ |Triangular Prism|```Volume```: ah+bh+ch+bl
```SA```: 1⁄2blh| |
+
+
+## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
+
+### 2D Objects
+
+ |Shape|Maximum Area|Minimum Perimeter|
+ |:----|:-----------|:----------------|
+ |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
|
+
+
+## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
+
+### 2D Objects
+
+ |Shape|Maximum Area|Minimum Perimeter|
+ |:----|:-----------|:----------------|
+ |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
A = lw
Amax = (w)(w)
Amax = w2|A rectangle must be a square to minimaze the perimeter for a given area. The length is equal to the width.
P = 2(l+w)
Pmin = 2(w)(w)
Pmin = 2(2w)
Pmin = 4w|
+ |3-sided rectangle|l = 2w
A = lw
Amax = 2w(w)
Amax = 2w2|l = 2w
P = l+w2
Pmin = 2w+2w
Pmin = 4w|
+
+
+### 3D Objects
+
+ |3D Object|Maximum Volumne|Minimum Surface Area|
+ |:--------|:--------------|:-------------------|
+ |Cylinder(closed-top)|The cylinder must be similar to a cube where h = 2r
V = πr2h
Vmax = πr2(2r)
Vmax = 2πr3|The cylinder must be similar to a cube where h = 2r
SA = 2πr2+2πrh
SAmin = 2πr2+2πr(2r)
SAmin = 2πr2+4πr2
SAmin = 6πr2|
+ |Rectangular Prism(closed-top)|The prism must be a cube,
where l = w = h
V = lwh
Vmax = (w)(w)(w)
Vmax = w3|The prism must be a cube,
where l = w = h
SA = 2lh+2lw+2wh
SAmin = 2w2+2w2+2w2
SAmin = 6w2|
+ |Cylinder(open-top)|h = r
V = πr2h
Vmax = πr2(r)
Vmax = πr3|h = r
SA = πr2+2πrh
SAmin = πr2+2πr(r)
SAmin = πr2+2πr2
SAmin = 3πr2|
+ |Square-Based Rectangular Prism(open-top)|h = w/2
V = lwh
Vmax = (w)(w)(w⁄2)
Vmax = w3⁄2|h = w/2
SA = w2+4wh
SAmin = w2+4w(w⁄2)
SAmin = w2+2w2
SAmin = 3w2|
+
+## Labelling
+- Given any polygons, labelling the vertices must always:
+ 1. use ```CAPITAL LETTERS```
+ 2. they have to be labeled in ```clockwise``` or ```counter-clockwise``` directions
+- For a triangle, the side lengths are labeled in ```LOWERCASE LETTERS``` associated to the opposite side of the vertex
+
+-  +
+## Median
+- Each median divides the triangle into 2 smaller triangles of equal area
+- The centroid is exactly
+
+## Median
+- Each median divides the triangle into 2 smaller triangles of equal area
+- The centroid is exactly  the way of each median from the vertex, or
the way of each median from the vertex, or  the way from the midpoint of the opposite side, or ```2:1``` ratio
+- The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
+
+-
the way from the midpoint of the opposite side, or ```2:1``` ratio
+- The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
+
+-  +
+## Terms:
+- ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+- ```Orthocenter```: where all 3 altitudes of the triangle intersect
+ -
+
+## Terms:
+- ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+- ```Orthocenter```: where all 3 altitudes of the triangle intersect
+ -  +- ```Midpoint```: A point on a line where the length of either side of the point are equal
+- ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+- ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+- ```Centroid```: The intersection of the 3 medians of a triangle
+ -
+- ```Midpoint```: A point on a line where the length of either side of the point are equal
+- ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+- ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+- ```Centroid```: The intersection of the 3 medians of a triangle
+ -  +
+## Proportionality theorem:
+- The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+- Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+- The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+-
+
+## Proportionality theorem:
+- The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+- Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+- The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+-  +
+## Tips
+- Make sure to know your optimization formualas
+- Read the word problems carefully, determine which formual to use
+- Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
+- To find ```missing area```, take what you have, subtract what you don't want
+- Don't be afraid to draw lines to help you solve the problem
+
+
+# Unit 5: Analytical Geometry and Linear Relations
+- ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
+- ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
+
+## Slope and Equation of Line
+- ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```the rate of change```
+- ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
+- ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
+- ```Y-intercept Form```: **y = mx + b**
+- ```Point-slope Form```: **y2-y1 = m(x2-x1)**
+- The slope of a vertical lines is undefined
+- The slope of a horizontal line is 0
+- Parallel lines have the ```same slope```
+- Perpendicular slopes are negative reciprocals
+
+## Relations
+- A relation can be described using
+ 1. Table of Values (see below)
+ 2. Equations (y = 3x + 5)
+ 3. Graphs (Graphing the equation)
+ 4. Words
+- When digging into the earth, the temperature rises according to the
+- following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
+- degrees and **h** is the depth in meters.
+
+## Perpendicular Lines
+- To find the perpendicular slope, you will need to find the slope point
+- Formula: slope1 × slope2 = -1
+- Notation: m⊥
+-
+
+## Tips
+- Make sure to know your optimization formualas
+- Read the word problems carefully, determine which formual to use
+- Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
+- To find ```missing area```, take what you have, subtract what you don't want
+- Don't be afraid to draw lines to help you solve the problem
+
+
+# Unit 5: Analytical Geometry and Linear Relations
+- ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
+- ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
+
+## Slope and Equation of Line
+- ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```the rate of change```
+- ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
+- ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
+- ```Y-intercept Form```: **y = mx + b**
+- ```Point-slope Form```: **y2-y1 = m(x2-x1)**
+- The slope of a vertical lines is undefined
+- The slope of a horizontal line is 0
+- Parallel lines have the ```same slope```
+- Perpendicular slopes are negative reciprocals
+
+## Relations
+- A relation can be described using
+ 1. Table of Values (see below)
+ 2. Equations (y = 3x + 5)
+ 3. Graphs (Graphing the equation)
+ 4. Words
+- When digging into the earth, the temperature rises according to the
+- following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
+- degrees and **h** is the depth in meters.
+
+## Perpendicular Lines
+- To find the perpendicular slope, you will need to find the slope point
+- Formula: slope1 × slope2 = -1
+- Notation: m⊥
+-  +
+
+## Definitions
+- ```Parallel```: 2 lines with the same slope
+- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+- ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+- ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+- ```Collinear Points```: points that line on the same straight line
+
+## Variables
+- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+## Statistics
+- ```Interpolation```: Data **inside** the given data set range.
+- ```Extrapolation```: Data **outside** the data set range.
+- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+- and it represents the trend of a graph.
+- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+## Time - Distance Graph
+- Time is the independent variable and distance is the dependent variable
+- You can't go backwards on the x-axis, as you can't go back in time
+- Plot the points accordingly
+- Draw the lines accordingly
+-
+
+
+## Definitions
+- ```Parallel```: 2 lines with the same slope
+- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+- ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+- ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+- ```Collinear Points```: points that line on the same straight line
+
+## Variables
+- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+## Statistics
+- ```Interpolation```: Data **inside** the given data set range.
+- ```Extrapolation```: Data **outside** the data set range.
+- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+- and it represents the trend of a graph.
+- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+## Time - Distance Graph
+- Time is the independent variable and distance is the dependent variable
+- You can't go backwards on the x-axis, as you can't go back in time
+- Plot the points accordingly
+- Draw the lines accordingly
+-  +
+**Direction is always referring to:**
+
+ 1. ```go towards home```
+ 2. ```going away from home```
+ 3. ```stop```
+
+## Scatterplot and Line of Best Fit
+- A scatterplot graph is there to show the relation between two variables in a table of values.
+- A line of best fit is a straight line that describes the relation between two variables.
+- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+-
+
+**Direction is always referring to:**
+
+ 1. ```go towards home```
+ 2. ```going away from home```
+ 3. ```stop```
+
+## Scatterplot and Line of Best Fit
+- A scatterplot graph is there to show the relation between two variables in a table of values.
+- A line of best fit is a straight line that describes the relation between two variables.
+- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+-  +
+### How To Determine the Equation Of a Line of Best Fit
+ 1. Find two points **```ON```** the ```line of best fit```
+ 2. Determine the ```slope``` using the two points
+ 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
+
+## Table of values
+- To find first differences or any points on the line, you can use a ```table of values```
+
+ | y | x |First Difference|
+ |:--|:--|:---------------|
+ |-1|-2|.....|
+ |0|-1|(-1)-(-2) = 1|
+|1|0|0 - (-1) = 1|
+|2|1|1 - 0 = 1|
+|3|2|2 - 1 = 1|
+|4|3|3 - 2 = 1|
+
+## Tips
+- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+- Draw your ```Line of Best Fit``` correctly
+- Read the word problems carefully, and make sure you understand it when graphing things
+- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+- Label your lines
+
+# Unit 6: System of Equations
+
+## Linear System
+- Two or more equation that you are working on all together at once on the same set of axes.
+- The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+- The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+- In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+- when **Profit = 0**. There is no gain or loss.
+
+### Number of Solutions
+-
+
+### How To Determine the Equation Of a Line of Best Fit
+ 1. Find two points **```ON```** the ```line of best fit```
+ 2. Determine the ```slope``` using the two points
+ 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
+
+## Table of values
+- To find first differences or any points on the line, you can use a ```table of values```
+
+ | y | x |First Difference|
+ |:--|:--|:---------------|
+ |-1|-2|.....|
+ |0|-1|(-1)-(-2) = 1|
+|1|0|0 - (-1) = 1|
+|2|1|1 - 0 = 1|
+|3|2|2 - 1 = 1|
+|4|3|3 - 2 = 1|
+
+## Tips
+- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+- Draw your ```Line of Best Fit``` correctly
+- Read the word problems carefully, and make sure you understand it when graphing things
+- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+- Label your lines
+
+# Unit 6: System of Equations
+
+## Linear System
+- Two or more equation that you are working on all together at once on the same set of axes.
+- The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+- The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+- In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+- when **Profit = 0**. There is no gain or loss.
+
+### Number of Solutions
+-  +
+## Discriminant
+- The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+- coefficients and constant of a quadratic equation: **y = ax2 + bx + c**
+- D = b2 - 4ac
+- D > 0 ```(2 distinct real solutions)```
+- D = 0 ```(1 real solution)```
+- D < 0 ```(no real solutions)```
+
+-
+
+## Discriminant
+- The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
+- coefficients and constant of a quadratic equation: **y = ax2 + bx + c**
+- D = b2 - 4ac
+- D > 0 ```(2 distinct real solutions)```
+- D = 0 ```(1 real solution)```
+- D < 0 ```(no real solutions)```
+
+-  +
+## Solving Linear-Quadratic Systems
+- To find the point of intersection, do the following:
+ 1. Isolate both equations for ```y```
+ 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+ 3. Simplify and put everything on one side and equal to zero on the other side
+ 4. Factor
+ 5. Use zero-product property to solve for all possible x-values
+ 6. Subsitute the x-values to one of the original equations to solve for all y-values
+ 7. State a conclusion / the solution
+
+-
+
+## Solving Linear-Quadratic Systems
+- To find the point of intersection, do the following:
+ 1. Isolate both equations for ```y```
+ 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+ 3. Simplify and put everything on one side and equal to zero on the other side
+ 4. Factor
+ 5. Use zero-product property to solve for all possible x-values
+ 6. Subsitute the x-values to one of the original equations to solve for all y-values
+ 7. State a conclusion / the solution
+
+-  +
+- There are 3 possible cases
+- In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
+
+
+# Ways to solve Systems of Equations
+ 1. Subsitution
+ - Here we eliminate a variable by subbing in another variable from another equation
+ - We usually do this method if a variable is easily isolated
+ - Example:
+ - ```
+ y = x + 10 (1)
+ x + y + 34 = 40 (2)
+ ```
+ We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
+ ```x + (x + 10) + 34 = 40```
+ ```2x + 44 = 40```
+ ```2x = -4```
+ ```x = -2```
+ Then solve for ```y```
+ ```y = -2 + 10```
+ ```y = -8```
+
+ 2. Elimination
+ - Here we eliminate a variable by basically eliminate a variable from an equation
+ - We usually use this method first when the variables are not easily isolated, then use subsitution to solve
+ - Example:
+ - ```
+ 2x + 3y = 10 (1)
+ 4x + 3y = 14 (2)
+ ```
+ We can then use elimination
+ ```
+ 4x + 3y = 14
+ 2x + 3y = 10
+ ------------
+ 2x + 0 = 4
+ x = 2
+ ```
+ Then sub the value of ```x``` into an original equation and solve for ```y```
+ ```2(2) + 3y = 10```
+ ```3y = 6```
+ ```y = 2```
+
+3. Graphing
+- we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
+
+## Solving Systems of Linear Inequalities
+- Find the intersection region as the ```solution```.
+- ## If
+
+ - | |Use ```Dash``` line|Use ```Solid line```|
+ |:-|:------------------|:-------------------|
+ |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
+ |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
+
+- ## If
+
+ - |x > a
+
+- There are 3 possible cases
+- In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
+
+
+# Ways to solve Systems of Equations
+ 1. Subsitution
+ - Here we eliminate a variable by subbing in another variable from another equation
+ - We usually do this method if a variable is easily isolated
+ - Example:
+ - ```
+ y = x + 10 (1)
+ x + y + 34 = 40 (2)
+ ```
+ We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
+ ```x + (x + 10) + 34 = 40```
+ ```2x + 44 = 40```
+ ```2x = -4```
+ ```x = -2```
+ Then solve for ```y```
+ ```y = -2 + 10```
+ ```y = -8```
+
+ 2. Elimination
+ - Here we eliminate a variable by basically eliminate a variable from an equation
+ - We usually use this method first when the variables are not easily isolated, then use subsitution to solve
+ - Example:
+ - ```
+ 2x + 3y = 10 (1)
+ 4x + 3y = 14 (2)
+ ```
+ We can then use elimination
+ ```
+ 4x + 3y = 14
+ 2x + 3y = 10
+ ------------
+ 2x + 0 = 4
+ x = 2
+ ```
+ Then sub the value of ```x``` into an original equation and solve for ```y```
+ ```2(2) + 3y = 10```
+ ```3y = 6```
+ ```y = 2```
+
+3. Graphing
+- we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
+
+## Solving Systems of Linear Inequalities
+- Find the intersection region as the ```solution```.
+- ## If
+
+ - | |Use ```Dash``` line|Use ```Solid line```|
+ |:-|:------------------|:-------------------|
+ |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
+ |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
+
+- ## If
+
+ - |x > a
x ≥ a|
+ |:------------------|
+ - |shade the region on the **right**|
+
+- ## If
+
+ - |x < a
x ≤ a|
+ - |:------------------|
+ - |shade the region on the **left**|
+
+- Step 1. change all inequalities to ```y-intercept form```
+- Step 2. graph the line
+- Step 3. shade the region where all the regions overlap
+
+-  +
+
+## Tips
+- Read the questions carefully and model the system of equations correctly
+- Be sure to name your equations
+- Label your lines
# General Tips
-> Be sure to watch out for units, like ```cm``` or ```km```
-> Watch out for ```+/-```
-> Be sure to reverse the operation when moving things to the other side of the equation
-> Make sure to have a proper scale for graphs
-> Read question carefully and use the appropriate tools to solve
-> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+- Be sure to watch out for units, like ```cm``` or ```km```
+- Watch out for ```+/-```
+- Be sure to reverse the operation when moving things to the other side of the equation
+- Make sure to have a proper scale for graphs
+- Read question carefully and use the appropriate tools to solve
+- **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
-> ## Word Problems
->> Read carefully
->> model equations correctly
->> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
->> ```Lets``` Statement
->> ```Conclusion```
+## Word Problems
+- Read carefully
+- model equations correctly
+- ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+- ```Lets``` Statement
+- ```Conclusion```
-> ## Graph Problems
->> Look up on tips in units (5) and (6)
->> be sure to use a ruler when graphing
+## Graph Problems
+- Look up on tips in units (5) and (6)
+- be sure to use a ruler when graphing
-> ## System of Equations
->> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+## System of Equations
+- When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
-> Ryan Mark - He helped provide alot of information for me
-> Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
-> Magicalsoup - ME!
+- Ryan Mark - He helped provide alot of information for me
+- Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
+- Magicalsoup - ME!
+
+
+## Tips
+- Read the questions carefully and model the system of equations correctly
+- Be sure to name your equations
+- Label your lines
# General Tips
-> Be sure to watch out for units, like ```cm``` or ```km```
-> Watch out for ```+/-```
-> Be sure to reverse the operation when moving things to the other side of the equation
-> Make sure to have a proper scale for graphs
-> Read question carefully and use the appropriate tools to solve
-> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+- Be sure to watch out for units, like ```cm``` or ```km```
+- Watch out for ```+/-```
+- Be sure to reverse the operation when moving things to the other side of the equation
+- Make sure to have a proper scale for graphs
+- Read question carefully and use the appropriate tools to solve
+- **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
-> ## Word Problems
->> Read carefully
->> model equations correctly
->> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
->> ```Lets``` Statement
->> ```Conclusion```
+## Word Problems
+- Read carefully
+- model equations correctly
+- ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+- ```Lets``` Statement
+- ```Conclusion```
-> ## Graph Problems
->> Look up on tips in units (5) and (6)
->> be sure to use a ruler when graphing
+## Graph Problems
+- Look up on tips in units (5) and (6)
+- be sure to use a ruler when graphing
-> ## System of Equations
->> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+## System of Equations
+- When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
-> Ryan Mark - He helped provide alot of information for me
-> Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
-> Magicalsoup - ME!
+- Ryan Mark - He helped provide alot of information for me
+- Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
+- Magicalsoup - ME!
 -
-> ## Interval Notation
->> A notation that represents an interval as a pair of numbers.
->> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
->> ```|``` means ```such that```
->> ```E``` or ∈ means ```element of```
->> ```N``` represents **Natural Numbers** (N = {x | x > 0, x ∈ Z})
->> ```W``` represents **Whole Numbers** (W = {x | x ≥ 0, x ∈ Z})
->> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
->> ```Q``` represents **Rational Numbers** (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
-
->> | Symbol | Meaning |
->> |:------:|:-------:|
->> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
->> | [a, b] | Inclusive |
->> | a ∪ b | Union (or) |
->> | a ∩ b | Intersection (and) |
-
-> ## Pythgorean Theorem
->> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
->> a2 + b2 = c2
-
->>
-
-> ## Interval Notation
->> A notation that represents an interval as a pair of numbers.
->> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
->> ```|``` means ```such that```
->> ```E``` or ∈ means ```element of```
->> ```N``` represents **Natural Numbers** (N = {x | x > 0, x ∈ Z})
->> ```W``` represents **Whole Numbers** (W = {x | x ≥ 0, x ∈ Z})
->> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
->> ```Q``` represents **Rational Numbers** (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
-
->> | Symbol | Meaning |
->> |:------:|:-------:|
->> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
->> | [a, b] | Inclusive |
->> | a ∪ b | Union (or) |
->> | a ∩ b | Intersection (and) |
-
-> ## Pythgorean Theorem
->> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
->> a2 + b2 = c2
-
->>  ->>>
->>>  |
| |
+-
|
+-  +-
+-  ->> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+ | Rule | Description| Example |
+ |:----:|:----------:|:-------:|
+ |Product|am × an = an+m|23 × 22 = 25|
+ |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
+ |Power of a Power|(am)n = amn|(23)2 = 26|
+ |Power of a Quotient|
->> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
+ | Rule | Description| Example |
+ |:----:|:----------:|:-------:|
+ |Product|am × an = an+m|23 × 22 = 25|
+ |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
+ |Power of a Power|(am)n = amn|(23)2 = 26|
+ |Power of a Quotient| |
| |
+
+**Note:**
+- Exponential Form --> Expanded Form
+- 64 = 6 × 6 × 6 × 6
+
+## Scientific Notation
+- They convey accuracy and precision. It can either be written as its original number or in scientific notation:
+- 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
+- In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
+- Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
+- When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+
+-
|
+
+**Note:**
+- Exponential Form --> Expanded Form
+- 64 = 6 × 6 × 6 × 6
+
+## Scientific Notation
+- They convey accuracy and precision. It can either be written as its original number or in scientific notation:
+- 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
+- In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
+- Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
+- When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
+
+-  +
+- **Remember**: For scientific notation, round to ```3 significant``` digits
+
+## Rates, Ratio and Percent
+- ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+- Examples: ```a:b, a:b:c, a/b, a to b ```
+
+- ```Rates```: A comparison of quantities expressed in different units.
+- Example: ```10km/hour```
+
+- ```Percent```: A fraction or ratio in which the denominator is 100
+- Examples: ```50%, 240/100```
+
+## Number Lines
+- a line that goes from a point to another point, a way to visualize set notations and the like
+-
+
+- **Remember**: For scientific notation, round to ```3 significant``` digits
+
+## Rates, Ratio and Percent
+- ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
+- Examples: ```a:b, a:b:c, a/b, a to b ```
+
+- ```Rates```: A comparison of quantities expressed in different units.
+- Example: ```10km/hour```
+
+- ```Percent```: A fraction or ratio in which the denominator is 100
+- Examples: ```50%, 240/100```
+
+## Number Lines
+- a line that goes from a point to another point, a way to visualize set notations and the like
+-  +- A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
-> ## Tips
->> Watch out for the ```+/-``` signs
->> Make sure to review your knowledge of the exponent laws
->> For scientific notation, watch out for the decimal point
->> Use shortcut when multiplying fractions
+## Tips
+- Watch out for the ```+/-``` signs
+- Make sure to review your knowledge of the exponent laws
+- For scientific notation, watch out for the decimal point
+- Use shortcut when multiplying fractions
-# Polyomials (2)
-> ## Introduction to Polynomials
->> A ```variable``` is a letter that represents one or more numbers
->> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
->> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
-> ## Methods to solve a polynomial
->> 1. ```Combine like terms```
->> 2. ```Dividing polynomials```
->> 3. ```Multiplying polynomials```
+# Unit 2: Polyomials
+## Introduction to Polynomials
+- A ```variable``` is a letter that represents one or more numbers
+- An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
+- When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+## Methods to solve a polynomial
+ 1. ```Combine like terms```
+ 2. ```Dividing polynomials```
+ 3. ```Multiplying polynomials```
-> ## Simplifying Alegebraic Expressions
->> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+## Simplifying Alegebraic Expressions
+- An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
-> ## Factoring
->>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
->> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
->> (e.g 5x + 10 = 5(x + 2) ).
+## Factoring
+- Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+- equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+- (e.g 5x + 10 = 5(x + 2) ).
->> |Type of Polynomial|Definition|
->> |:-----------------|:---------|
->> |Monomial|Polynomial that only has one term|
->> |Binomial|Polynomial that only has 2 terms|
->> |Trinomial|polynomial that only has 3 terms|
+|Type of Polynomial|Definition|
+ |:-----------------|:---------|
+ |Monomial|Polynomial that only has one term|
+ |Binomial|Polynomial that only has 2 terms|
+ |Trinomial|polynomial that only has 3 terms|
->> |Type|Example|
->> |:--:|:-----:|
->> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
->> |Difference with Squares|a2-b2 = (a+b)(a-b)|
->> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
->> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
->> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
->> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+ |Type|Example|
+ |:--:|:-----:|
+ |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+ |Difference with Squares|a2-b2 = (a+b)(a-b)|
+ |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+ |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+ |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+ |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
-> ## Shortcuts
+## Shortcuts
->>
+- A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
-> ## Tips
->> Watch out for the ```+/-``` signs
->> Make sure to review your knowledge of the exponent laws
->> For scientific notation, watch out for the decimal point
->> Use shortcut when multiplying fractions
+## Tips
+- Watch out for the ```+/-``` signs
+- Make sure to review your knowledge of the exponent laws
+- For scientific notation, watch out for the decimal point
+- Use shortcut when multiplying fractions
-# Polyomials (2)
-> ## Introduction to Polynomials
->> A ```variable``` is a letter that represents one or more numbers
->> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
->> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
-> ## Methods to solve a polynomial
->> 1. ```Combine like terms```
->> 2. ```Dividing polynomials```
->> 3. ```Multiplying polynomials```
+# Unit 2: Polyomials
+## Introduction to Polynomials
+- A ```variable``` is a letter that represents one or more numbers
+- An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6. y + 8)```
+- When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
+## Methods to solve a polynomial
+ 1. ```Combine like terms```
+ 2. ```Dividing polynomials```
+ 3. ```Multiplying polynomials```
-> ## Simplifying Alegebraic Expressions
->> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
+## Simplifying Alegebraic Expressions
+- An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
-> ## Factoring
->>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
->> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
->> (e.g 5x + 10 = 5(x + 2) ).
+## Factoring
+- Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
+- equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
+- (e.g 5x + 10 = 5(x + 2) ).
->> |Type of Polynomial|Definition|
->> |:-----------------|:---------|
->> |Monomial|Polynomial that only has one term|
->> |Binomial|Polynomial that only has 2 terms|
->> |Trinomial|polynomial that only has 3 terms|
+|Type of Polynomial|Definition|
+ |:-----------------|:---------|
+ |Monomial|Polynomial that only has one term|
+ |Binomial|Polynomial that only has 2 terms|
+ |Trinomial|polynomial that only has 3 terms|
->> |Type|Example|
->> |:--:|:-----:|
->> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
->> |Difference with Squares|a2-b2 = (a+b)(a-b)|
->> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
->> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
->> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
->> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
+ |Type|Example|
+ |:--:|:-----:|
+ |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
+ |Difference with Squares|a2-b2 = (a+b)(a-b)|
+ |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
+ |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
+ |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
+ |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
-> ## Shortcuts
+## Shortcuts
->>  +-
+-  -> ## Foil / Rainbow Method
->>
-> ## Foil / Rainbow Method
->>  +## Foil / Rainbow Method
+-
+## Foil / Rainbow Method
+-  -> ## Definitions
->> ```Term``` a variable that may have coefficient(s) or a constant
->> ```Alebraic Expressions```: made up of one or more terms
->> ```Like-terms```: same variables raised to the same exponent
+## Definitions
+- ```Term``` a variable that may have coefficient(s) or a constant
+- ```Alebraic Expressions```: made up of one or more terms
+- ```Like-terms```: same variables raised to the same exponent
-> ## Tips
->> Be sure to factor fully
->> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
->> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
->> Remember your formulas
->> Simplify first, combine like terms
+## Tips
+- Be sure to factor fully
+- Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+- Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+- Remember your formulas
+- Simplify first, combine like terms
-# Solving Equations and Inequailties (3)
-> ## Equations
->> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
->> To ```solve``` and equation is to find the variable that makes the statement true
->> ### Methods to solve an equation
->>> 1. Expand and simplify both sides
->>> 2. Isolate using reverse order of operations
->>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+# Unit 3: Solving Equations and Inequailties
+
+## Equations
+- a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+- To ```solve``` and equation is to find the variable that makes the statement true
+### Methods to solve an equation
+ 1. Expand and simplify both sides
+ 2. Isolate using reverse order of operations
+ 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
->
-> ## Absolute Values
->> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->> equations will have the absolute bracket be positive while the other negative.
->> Absolute values are written in the form ```| x |```
->> where
->> if x > 0, | x | = x
->> if x = 0, | x | = 0
->> if x < 0, | x | = -x
+## Absolute Values
+- There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+- equations will have the absolute bracket be positive while the other negative.
+- Absolute values are written in the form ```| x |```
+- where
+ - if x > 0, | x | = x
+ - if x = 0, | x | = 0
+ - if x < 0, | x | = -x
-> ## Quadractic Equations
->> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
->> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
->> Solve quadratic equation by:
->> 1. Isolation
->> a(x+b)2 + k = 0
->> 2. Factor using zero-product property
->> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
->> (x-a)(x-b)=0
->> x = a, b
+## Quadractic Equations
+- ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+- ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+- Solve quadratic equation by:
->>
-> ## Definitions
->> ```Term``` a variable that may have coefficient(s) or a constant
->> ```Alebraic Expressions```: made up of one or more terms
->> ```Like-terms```: same variables raised to the same exponent
+## Definitions
+- ```Term``` a variable that may have coefficient(s) or a constant
+- ```Alebraic Expressions```: made up of one or more terms
+- ```Like-terms```: same variables raised to the same exponent
-> ## Tips
->> Be sure to factor fully
->> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
->> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
->> Remember your formulas
->> Simplify first, combine like terms
+## Tips
+- Be sure to factor fully
+- Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
+- Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
+- Remember your formulas
+- Simplify first, combine like terms
-# Solving Equations and Inequailties (3)
-> ## Equations
->> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
->> To ```solve``` and equation is to find the variable that makes the statement true
->> ### Methods to solve an equation
->>> 1. Expand and simplify both sides
->>> 2. Isolate using reverse order of operations
->>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
+# Unit 3: Solving Equations and Inequailties
+
+## Equations
+- a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
+- To ```solve``` and equation is to find the variable that makes the statement true
+### Methods to solve an equation
+ 1. Expand and simplify both sides
+ 2. Isolate using reverse order of operations
+ 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
->
-> ## Absolute Values
->> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
->> equations will have the absolute bracket be positive while the other negative.
->> Absolute values are written in the form ```| x |```
->> where
->> if x > 0, | x | = x
->> if x = 0, | x | = 0
->> if x < 0, | x | = -x
+## Absolute Values
+- There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
+- equations will have the absolute bracket be positive while the other negative.
+- Absolute values are written in the form ```| x |```
+- where
+ - if x > 0, | x | = x
+ - if x = 0, | x | = 0
+ - if x < 0, | x | = -x
-> ## Quadractic Equations
->> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
->> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
->> Solve quadratic equation by:
->> 1. Isolation
->> a(x+b)2 + k = 0
->> 2. Factor using zero-product property
->> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
->> (x-a)(x-b)=0
->> x = a, b
+## Quadractic Equations
+- ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
+- ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
+- Solve quadratic equation by:
->>  + 1. Isolation
+ - a(x+b)2 + k = 0
+ 2. Factor using zero-product property
+ - ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+ - (x-a)(x-b)=0
+ - x = a, b
->> Note:
->> √x2 = ± x (There are 2 possible solutions)
->> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+-
+ 1. Isolation
+ - a(x+b)2 + k = 0
+ 2. Factor using zero-product property
+ - ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
+ - (x-a)(x-b)=0
+ - x = a, b
->> Note:
->> √x2 = ± x (There are 2 possible solutions)
->> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
+-  +
+**Note:**
+- √x2 = ± x (There are 2 possible solutions)
+- ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
-> ## Tips
->> ```Absolute Values``` can have 2 solutions
->> ```Quadratics``` can also have 2 solutions
->> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
+## Tips
+- ```Absolute Values``` can have 2 solutions
+- ```Quadratics``` can also have 2 solutions
+- Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
-# Measurement and Geometry (4)
-> ## Angle Theorems
-> 1. ```Transversal Parallel Line Theorems``` (TPT)
-> a. Alternate Angles are Equal ```(Z-Pattern)```
-> b. Corresponding Angles Equal ```(F-Pattern)```
-> c. Interior Angles add up to 180 ```(C-Pattern)```
+# Unit 4: Measurement and Geometry
+## Angle Theorems
+
+1. ```Transversal Parallel Line Theorems``` (TPT)
+ a. Alternate Angles are Equal ```(Z-Pattern)```
+ b. Corresponding Angles Equal ```(F-Pattern)```
+ c. Interior Angles add up to 180 ```(C-Pattern)```
>
+
+**Note:**
+- √x2 = ± x (There are 2 possible solutions)
+- ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
-> ## Tips
->> ```Absolute Values``` can have 2 solutions
->> ```Quadratics``` can also have 2 solutions
->> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
+## Tips
+- ```Absolute Values``` can have 2 solutions
+- ```Quadratics``` can also have 2 solutions
+- Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
-# Measurement and Geometry (4)
-> ## Angle Theorems
-> 1. ```Transversal Parallel Line Theorems``` (TPT)
-> a. Alternate Angles are Equal ```(Z-Pattern)```
-> b. Corresponding Angles Equal ```(F-Pattern)```
-> c. Interior Angles add up to 180 ```(C-Pattern)```
+# Unit 4: Measurement and Geometry
+## Angle Theorems
+
+1. ```Transversal Parallel Line Theorems``` (TPT)
+ a. Alternate Angles are Equal ```(Z-Pattern)```
+ b. Corresponding Angles Equal ```(F-Pattern)```
+ c. Interior Angles add up to 180 ```(C-Pattern)```
>  -> 2. ```Supplementary Angle Triangle``` (SAT)
-> - When two angles add up to 180 degrees
+2. ```Supplementary Angle Triangle``` (SAT)
+ - When two angles add up to 180 degrees
->
-> 2. ```Supplementary Angle Triangle``` (SAT)
-> - When two angles add up to 180 degrees
+2. ```Supplementary Angle Triangle``` (SAT)
+ - When two angles add up to 180 degrees
->  + -
+ -  -> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
-> - Two lines intersect, two angles form opposite. They have equal measures
+3. ```Opposite Angle Theorem (OAT)``` (OAT)
+ - Two lines intersect, two angles form opposite. They have equal measures
->
-> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
-> - Two lines intersect, two angles form opposite. They have equal measures
+3. ```Opposite Angle Theorem (OAT)``` (OAT)
+ - Two lines intersect, two angles form opposite. They have equal measures
->  + -
+ -  -> 4. ```Complementary Angle Theorem``` (CAT)
-> - The sum of two angles that add up to 90 degrees
+4. ```Complementary Angle Theorem``` (CAT)
+ - The sum of two angles that add up to 90 degrees
->
-> 4. ```Complementary Angle Theorem``` (CAT)
-> - The sum of two angles that add up to 90 degrees
+4. ```Complementary Angle Theorem``` (CAT)
+ - The sum of two angles that add up to 90 degrees
->  + -
+ -  -> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
-> - The sum of the three interior angles of any triangle is 180 degrees
+5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+ - The sum of the three interior angles of any triangle is 180 degrees
->
-> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
-> - The sum of the three interior angles of any triangle is 180 degrees
+5. ```Angle Sum of a Triangle Theorem``` (ASTT)
+ - The sum of the three interior angles of any triangle is 180 degrees
->  + -
+ -  -> 6. ```Exterior Angle Theorem``` (EAT)
-> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+6. ```Exterior Angle Theorem``` (EAT)
+ - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
->
-> 6. ```Exterior Angle Theorem``` (EAT)
-> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
+6. ```Exterior Angle Theorem``` (EAT)
+ - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
->  + -
+ - -> 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+7. ``` Isosceles Triangle Theorem``` (ITT)
+ - The base angles in any isosceles triangle are equal
->
-> 7. ``` Isosceles Triangle Theorem``` (ITT)
-> - The base angles in any isosceles triangle are equal
+7. ``` Isosceles Triangle Theorem``` (ITT)
+ - The base angles in any isosceles triangle are equal
->  + -
+ -  -> 8. ```Sum of The Interior Angle of a Polygon```
-> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+8. ```Sum of The Interior Angle of a Polygon```
+ - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
->
-> 8. ```Sum of The Interior Angle of a Polygon```
-> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
+8. ```Sum of The Interior Angle of a Polygon```
+ - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
->  + -
+ -  -> 9. ```Exterior Angles of a Convex Polygon```
-> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+9. ```Exterior Angles of a Convex Polygon```
+ - The sum of the exterior angle of any convex polygon is always ```360 degrees```
->
-> 9. ```Exterior Angles of a Convex Polygon```
-> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
+9. ```Exterior Angles of a Convex Polygon```
+ - The sum of the exterior angle of any convex polygon is always ```360 degrees```
->  + -
+ -  -> ## Properties of Quadrilaterals
->> Determine the shape using the properties of it
+## Properties of Quadrilaterals
+- Determine the shape using the properties of it
->> |Figure|Properties|
->> |:-----|:---------|
->> |Scalene Triangle|no sides equal|Length of line segment|
->> |Isosceles Triangle| two sides equal|Length of line segment|
->> |Equilateral Triangle|All sides equal|Length of line segment|
->> |Right Angle Triangle|Two sides are perpendicular to each other|
->> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
->> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
->> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
->> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
->> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
->> |Kite|The diagonals are perpendicular|
-
-> ## 2D Geometry Equations
->> |Shape|Formula|Picture|
->> |:----|:------|:------|
->> |Rectangle|```Area```: lw
-> ## Properties of Quadrilaterals
->> Determine the shape using the properties of it
+## Properties of Quadrilaterals
+- Determine the shape using the properties of it
->> |Figure|Properties|
->> |:-----|:---------|
->> |Scalene Triangle|no sides equal|Length of line segment|
->> |Isosceles Triangle| two sides equal|Length of line segment|
->> |Equilateral Triangle|All sides equal|Length of line segment|
->> |Right Angle Triangle|Two sides are perpendicular to each other|
->> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
->> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
->> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
->> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
->> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
->> |Kite|The diagonals are perpendicular|
-
-> ## 2D Geometry Equations
->> |Shape|Formula|Picture|
->> |:----|:------|:------|
->> |Rectangle|```Area```: lw  -
-> ## Median
->> Each median divides the triangle into 2 smaller triangles of equal area
->> The centroid is exactly
-
-> ## Median
->> Each median divides the triangle into 2 smaller triangles of equal area
->> The centroid is exactly  -
-> ## Terms:
->> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
->> ```Orthocenter```: where all 3 altitudes of the triangle intersect
->>>
-
-> ## Terms:
->> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
->> ```Orthocenter```: where all 3 altitudes of the triangle intersect
->>>  ->> ```Midpoint```: A point on a line where the length of either side of the point are equal
->> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
->> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
->> ```Centroid```: The intersection of the 3 medians of a triangle
->>>
->> ```Midpoint```: A point on a line where the length of either side of the point are equal
->> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
->> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
->> ```Centroid```: The intersection of the 3 medians of a triangle
->>>  -
-> ## Proportionality theorem:
->> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
->> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
->> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
->>
-
-> ## Proportionality theorem:
->> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
->> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
->> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
->>  -
-
-> ## Definitions
->> ```Parallel```: 2 lines with the same slope
->> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
->> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
->> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
->> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
->> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
->> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
->> ```Collinear Points```: points that line on the same straight line
-
-> ## Variables
->> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
->> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
-
-> ## Statistics
->> ```Interpolation```: Data **inside** the given data set range.
->> ```Extrapolation```: Data **outside** the data set range.
->> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
->> and it represents the trend of a graph.
->> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
->> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
-
-> ## Time - Distance Graph
->> Time is the independent variable and distance is the dependent variable
->> You can't go backwards on the x-axis, as you can't go back in time
->> Plot the points accordingly
->> Draw the lines accordingly
->>
-
-
-> ## Definitions
->> ```Parallel```: 2 lines with the same slope
->> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
->> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
->> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
->> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
->> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
->> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
->> ```Collinear Points```: points that line on the same straight line
-
-> ## Variables
->> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
->> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
-
-> ## Statistics
->> ```Interpolation```: Data **inside** the given data set range.
->> ```Extrapolation```: Data **outside** the data set range.
->> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
->> and it represents the trend of a graph.
->> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
->> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
-
-> ## Time - Distance Graph
->> Time is the independent variable and distance is the dependent variable
->> You can't go backwards on the x-axis, as you can't go back in time
->> Plot the points accordingly
->> Draw the lines accordingly
->>  -
->> **Direction is always referring to:**
-
->> 1. ```go towards home```
->> 2. ```going away from home```
->> 3. ```stop```
-
-> ## Scatterplot and Line of Best Fit
->> A scatterplot graph is there to show the relation between two variables in a table of values.
->> A line of best fit is a straight line that describes the relation between two variables.
->> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>
-
->> **Direction is always referring to:**
-
->> 1. ```go towards home```
->> 2. ```going away from home```
->> 3. ```stop```
-
-> ## Scatterplot and Line of Best Fit
->> A scatterplot graph is there to show the relation between two variables in a table of values.
->> A line of best fit is a straight line that describes the relation between two variables.
->> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
->>  -
->> ### How To Determine the Equation Of a Line of Best Fit
->> 1. Find two points **```ON```** the ```line of best fit```
->> 2. Determine the ```slope``` using the two points
->> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
-
-> ## Table of values
->> To find first differences or any points on the line, you can use a ```table of values```
-
->>| y | x |First Difference|
->>|:--|:--|:---------------|
->>|-1|-2|.....|
->>|0|-1|(-1)-(-2) = 1|
->>|1|0|0 - (-1) = 1|
->>|2|1|1 - 0 = 1|
->>|3|2|2 - 1 = 1|
->>|4|3|3 - 2 = 1|
-
-> ## Tips
->> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
->> Draw your ```Line of Best Fit``` correctly
->> Read the word problems carefully, and make sure you understand it when graphing things
->> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
->> Label your lines
-
-# System of Equations (6)
-
-> ## Linear System
->> Two or more equation that you are working on all together at once on the same set of axes.
->> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
->> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
-
->> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
->> when **Profit = 0**. There is no gain or loss.
-
->> ### Number of Solutions
->>>
-
->> ### How To Determine the Equation Of a Line of Best Fit
->> 1. Find two points **```ON```** the ```line of best fit```
->> 2. Determine the ```slope``` using the two points
->> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
-
-> ## Table of values
->> To find first differences or any points on the line, you can use a ```table of values```
-
->>| y | x |First Difference|
->>|:--|:--|:---------------|
->>|-1|-2|.....|
->>|0|-1|(-1)-(-2) = 1|
->>|1|0|0 - (-1) = 1|
->>|2|1|1 - 0 = 1|
->>|3|2|2 - 1 = 1|
->>|4|3|3 - 2 = 1|
-
-> ## Tips
->> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
->> Draw your ```Line of Best Fit``` correctly
->> Read the word problems carefully, and make sure you understand it when graphing things
->> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
->> Label your lines
-
-# System of Equations (6)
-
-> ## Linear System
->> Two or more equation that you are working on all together at once on the same set of axes.
->> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
->> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
-
->> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
->> when **Profit = 0**. There is no gain or loss.
-
->> ### Number of Solutions
->>>  -
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->>
-
-> ## Solving Linear-Quadratic Systems
->> To find the point of intersection, do the following:
->> 1. Isolate both equations for ```y```
->> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
->> 3. Simplify and put everything on one side and equal to zero on the other side
->> 4. Factor
->> 5. Use zero-product property to solve for all possible x-values
->> 6. Subsitute the x-values to one of the original equations to solve for all y-values
->> 7. State a conclusion / the solution
-
->>  -
-
-> ## Tips
->> Read the questions carefully and model the system of equations correctly
->> Be sure to name your equations
->> Label your lines
+ |Figure|Properties|
+ |:-----|:---------|
+ |Scalene Triangle|no sides equal|Length of line segment|
+ |Isosceles Triangle| two sides equal|Length of line segment|
+ |Equilateral Triangle|All sides equal|Length of line segment|
+ |Right Angle Triangle|Two sides are perpendicular to each other|
+ |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+ |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+ |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+ |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+ |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+ |Kite|The diagonals are perpendicular|
+
+## 2D Geometry Equations
+ |Shape|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangle|```Area```: lw
-
-
-> ## Tips
->> Read the questions carefully and model the system of equations correctly
->> Be sure to name your equations
->> Label your lines
+ |Figure|Properties|
+ |:-----|:---------|
+ |Scalene Triangle|no sides equal|Length of line segment|
+ |Isosceles Triangle| two sides equal|Length of line segment|
+ |Equilateral Triangle|All sides equal|Length of line segment|
+ |Right Angle Triangle|Two sides are perpendicular to each other|
+ |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
+ |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
+ |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
+ |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
+ |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
+ |Kite|The diagonals are perpendicular|
+
+## 2D Geometry Equations
+ |Shape|Formula|Picture|
+ |:----|:------|:------|
+ |Rectangle|```Area```: lw  +
+## Median
+- Each median divides the triangle into 2 smaller triangles of equal area
+- The centroid is exactly
+
+## Median
+- Each median divides the triangle into 2 smaller triangles of equal area
+- The centroid is exactly  +
+## Terms:
+- ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+- ```Orthocenter```: where all 3 altitudes of the triangle intersect
+ -
+
+## Terms:
+- ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
+- ```Orthocenter```: where all 3 altitudes of the triangle intersect
+ -  +- ```Midpoint```: A point on a line where the length of either side of the point are equal
+- ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+- ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+- ```Centroid```: The intersection of the 3 medians of a triangle
+ -
+- ```Midpoint```: A point on a line where the length of either side of the point are equal
+- ```Median```: A line segment joining the vertex to the midpoint of the opposite side
+- ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
+- ```Centroid```: The intersection of the 3 medians of a triangle
+ -  +
+## Proportionality theorem:
+- The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+- Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+- The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+-
+
+## Proportionality theorem:
+- The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
+- Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
+- The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
+-  +
+
+## Definitions
+- ```Parallel```: 2 lines with the same slope
+- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+- ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+- ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+- ```Collinear Points```: points that line on the same straight line
+
+## Variables
+- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+## Statistics
+- ```Interpolation```: Data **inside** the given data set range.
+- ```Extrapolation```: Data **outside** the data set range.
+- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+- and it represents the trend of a graph.
+- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+## Time - Distance Graph
+- Time is the independent variable and distance is the dependent variable
+- You can't go backwards on the x-axis, as you can't go back in time
+- Plot the points accordingly
+- Draw the lines accordingly
+-
+
+
+## Definitions
+- ```Parallel```: 2 lines with the same slope
+- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
+- ```Domain```: The **ordered** set of all possible values of the independent variable (x).
+- ```Range```: The **ordered** set of all possible values of the dependent variable (y).
+- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
+- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
+- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
+- ```Collinear Points```: points that line on the same straight line
+
+## Variables
+- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
+- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
+
+## Statistics
+- ```Interpolation```: Data **inside** the given data set range.
+- ```Extrapolation```: Data **outside** the data set range.
+- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
+- and it represents the trend of a graph.
+- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
+- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
+
+## Time - Distance Graph
+- Time is the independent variable and distance is the dependent variable
+- You can't go backwards on the x-axis, as you can't go back in time
+- Plot the points accordingly
+- Draw the lines accordingly
+-  +
+**Direction is always referring to:**
+
+ 1. ```go towards home```
+ 2. ```going away from home```
+ 3. ```stop```
+
+## Scatterplot and Line of Best Fit
+- A scatterplot graph is there to show the relation between two variables in a table of values.
+- A line of best fit is a straight line that describes the relation between two variables.
+- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+-
+
+**Direction is always referring to:**
+
+ 1. ```go towards home```
+ 2. ```going away from home```
+ 3. ```stop```
+
+## Scatterplot and Line of Best Fit
+- A scatterplot graph is there to show the relation between two variables in a table of values.
+- A line of best fit is a straight line that describes the relation between two variables.
+- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
+-  +
+### How To Determine the Equation Of a Line of Best Fit
+ 1. Find two points **```ON```** the ```line of best fit```
+ 2. Determine the ```slope``` using the two points
+ 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
+
+## Table of values
+- To find first differences or any points on the line, you can use a ```table of values```
+
+ | y | x |First Difference|
+ |:--|:--|:---------------|
+ |-1|-2|.....|
+ |0|-1|(-1)-(-2) = 1|
+|1|0|0 - (-1) = 1|
+|2|1|1 - 0 = 1|
+|3|2|2 - 1 = 1|
+|4|3|3 - 2 = 1|
+
+## Tips
+- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+- Draw your ```Line of Best Fit``` correctly
+- Read the word problems carefully, and make sure you understand it when graphing things
+- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+- Label your lines
+
+# Unit 6: System of Equations
+
+## Linear System
+- Two or more equation that you are working on all together at once on the same set of axes.
+- The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+- The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+- In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+- when **Profit = 0**. There is no gain or loss.
+
+### Number of Solutions
+-
+
+### How To Determine the Equation Of a Line of Best Fit
+ 1. Find two points **```ON```** the ```line of best fit```
+ 2. Determine the ```slope``` using the two points
+ 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
+
+## Table of values
+- To find first differences or any points on the line, you can use a ```table of values```
+
+ | y | x |First Difference|
+ |:--|:--|:---------------|
+ |-1|-2|.....|
+ |0|-1|(-1)-(-2) = 1|
+|1|0|0 - (-1) = 1|
+|2|1|1 - 0 = 1|
+|3|2|2 - 1 = 1|
+|4|3|3 - 2 = 1|
+
+## Tips
+- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
+- Draw your ```Line of Best Fit``` correctly
+- Read the word problems carefully, and make sure you understand it when graphing things
+- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
+- Label your lines
+
+# Unit 6: System of Equations
+
+## Linear System
+- Two or more equation that you are working on all together at once on the same set of axes.
+- The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
+- The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
+
+- In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
+- when **Profit = 0**. There is no gain or loss.
+
+### Number of Solutions
+-  +
+## Solving Linear-Quadratic Systems
+- To find the point of intersection, do the following:
+ 1. Isolate both equations for ```y```
+ 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+ 3. Simplify and put everything on one side and equal to zero on the other side
+ 4. Factor
+ 5. Use zero-product property to solve for all possible x-values
+ 6. Subsitute the x-values to one of the original equations to solve for all y-values
+ 7. State a conclusion / the solution
+
+-
+
+## Solving Linear-Quadratic Systems
+- To find the point of intersection, do the following:
+ 1. Isolate both equations for ```y```
+ 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
+ 3. Simplify and put everything on one side and equal to zero on the other side
+ 4. Factor
+ 5. Use zero-product property to solve for all possible x-values
+ 6. Subsitute the x-values to one of the original equations to solve for all y-values
+ 7. State a conclusion / the solution
+
+-  +
+
+## Tips
+- Read the questions carefully and model the system of equations correctly
+- Be sure to name your equations
+- Label your lines
# General Tips
-> Be sure to watch out for units, like ```cm``` or ```km```
-> Watch out for ```+/-```
-> Be sure to reverse the operation when moving things to the other side of the equation
-> Make sure to have a proper scale for graphs
-> Read question carefully and use the appropriate tools to solve
-> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+- Be sure to watch out for units, like ```cm``` or ```km```
+- Watch out for ```+/-```
+- Be sure to reverse the operation when moving things to the other side of the equation
+- Make sure to have a proper scale for graphs
+- Read question carefully and use the appropriate tools to solve
+- **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
-> ## Word Problems
->> Read carefully
->> model equations correctly
->> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
->> ```Lets``` Statement
->> ```Conclusion```
+## Word Problems
+- Read carefully
+- model equations correctly
+- ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+- ```Lets``` Statement
+- ```Conclusion```
-> ## Graph Problems
->> Look up on tips in units (5) and (6)
->> be sure to use a ruler when graphing
+## Graph Problems
+- Look up on tips in units (5) and (6)
+- be sure to use a ruler when graphing
-> ## System of Equations
->> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+## System of Equations
+- When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
-> Ryan Mark - He helped provide alot of information for me
-> Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
-> Magicalsoup - ME!
+- Ryan Mark - He helped provide alot of information for me
+- Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
+- Magicalsoup - ME!
+
+
+## Tips
+- Read the questions carefully and model the system of equations correctly
+- Be sure to name your equations
+- Label your lines
# General Tips
-> Be sure to watch out for units, like ```cm``` or ```km```
-> Watch out for ```+/-```
-> Be sure to reverse the operation when moving things to the other side of the equation
-> Make sure to have a proper scale for graphs
-> Read question carefully and use the appropriate tools to solve
-> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
+- Be sure to watch out for units, like ```cm``` or ```km```
+- Watch out for ```+/-```
+- Be sure to reverse the operation when moving things to the other side of the equation
+- Make sure to have a proper scale for graphs
+- Read question carefully and use the appropriate tools to solve
+- **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
-> ## Word Problems
->> Read carefully
->> model equations correctly
->> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
->> ```Lets``` Statement
->> ```Conclusion```
+## Word Problems
+- Read carefully
+- model equations correctly
+- ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
+- ```Lets``` Statement
+- ```Conclusion```
-> ## Graph Problems
->> Look up on tips in units (5) and (6)
->> be sure to use a ruler when graphing
+## Graph Problems
+- Look up on tips in units (5) and (6)
+- be sure to use a ruler when graphing
-> ## System of Equations
->> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
+## System of Equations
+- When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
-> Ryan Mark - He helped provide alot of information for me
-> Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
-> Magicalsoup - ME!
+- Ryan Mark - He helped provide alot of information for me
+- Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
+- Magicalsoup - ME!