diff --git a/Grade 10/Math/MPM2DZ/Unit 4: Trigonometry.md b/Grade 10/Math/MPM2DZ/Unit 4: Trigonometry.md
index 825dfc9..695d464 100644
--- a/Grade 10/Math/MPM2DZ/Unit 4: Trigonometry.md
+++ b/Grade 10/Math/MPM2DZ/Unit 4: Trigonometry.md
@@ -1,3 +1,5 @@
+# Unit 4: Trigonometry
+
## Angle Theorems
1. ```Transversal Parallel Line Theorems``` (TPT)
@@ -55,12 +57,18 @@
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
+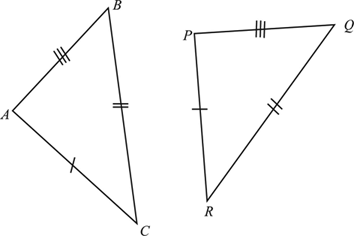 +
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
+
+
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
+ +
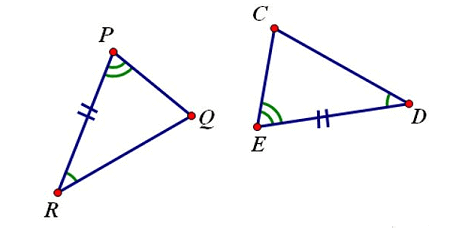
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
+
+
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
+ +
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
@@ -83,10 +91,101 @@ our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and
Three pairs of corresponding sides are in the **same ratio**
+
+
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
@@ -83,10 +91,101 @@ our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and
Three pairs of corresponding sides are in the **same ratio**
+ +
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
+
+
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
+ +
### Angle-Angle similarity (AA $`\sim`$)
-Two pairs of corresponding angles are equal.
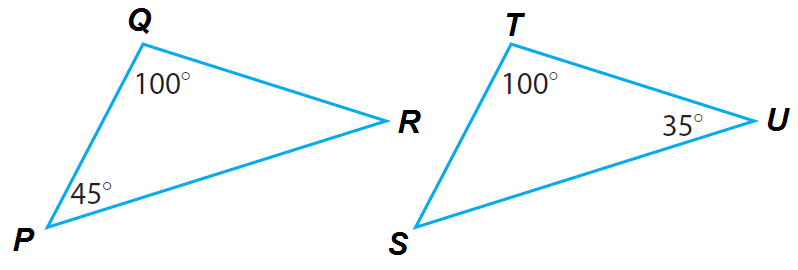
+Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
+
+
+
### Angle-Angle similarity (AA $`\sim`$)
-Two pairs of corresponding angles are equal.
+Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
+
+ +
+
+
+## Primary Trigonometry Ratios
+
+|Part Of Triangle|Property|
+|:---------------|:-------|
+|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
+|Opposite|The side opposite to the reference angle|
+|Adjacent|The side next to the reference agnle|
+
+**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
+
+### SOH CAH TOA
+
+**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
+
+**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
+
+**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
+
+## Angle Of Elevation And Depression
+
+| |Angle of Elevation|Angle of Depression|
+|:---------|:-----------------|:------------------|
+|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
+|Diagram|
+
+
+
+## Primary Trigonometry Ratios
+
+|Part Of Triangle|Property|
+|:---------------|:-------|
+|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
+|Opposite|The side opposite to the reference angle|
+|Adjacent|The side next to the reference agnle|
+
+**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
+
+### SOH CAH TOA
+
+**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
+
+**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
+
+**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
+
+## Angle Of Elevation And Depression
+
+| |Angle of Elevation|Angle of Depression|
+|:---------|:-----------------|:------------------|
+|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
+|Diagram| |
| |
+
+
+We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
+
+
|
+
+
+We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
+
+ +
+## Sine Law
+
+In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
+
+We can derive the formula further to get:
+- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
+- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
+- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
+
+Also, for some trigonometry identities:
+- $`\tan x = \dfrac{\sin x}{\cos x}`$
+- $`\sin^2 A + \cos^2 A = 1`$
+
+**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
+
+### Ambiguous Case
+The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
+
+In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
+
+
+|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
+|:---|:---------------------------|:--------|:-----------------------------|
+|1 |
+
+## Sine Law
+
+In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
+
+We can derive the formula further to get:
+- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
+- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
+- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
+
+Also, for some trigonometry identities:
+- $`\tan x = \dfrac{\sin x}{\cos x}`$
+- $`\sin^2 A + \cos^2 A = 1`$
+
+**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
+
+### Ambiguous Case
+The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
+
+In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
+
+
+|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
+|:---|:---------------------------|:--------|:-----------------------------|
+|1 | |$`a \lt h`$|no triangle exists|
+|2 |
|$`a \lt h`$|no triangle exists|
+|2 | |$`a = h`$|one triangle exists|
+|3 |
|$`a = h`$|one triangle exists|
+|3 |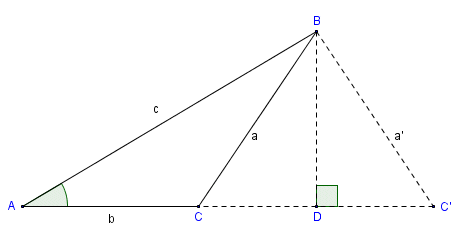 |$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
+|4 |
|$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
+|4 |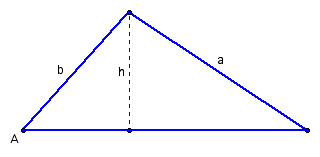 |$`a \ge b`$|one triangle exists|
+
+|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
+|:---|:----------------------------|:--------|:-----------------------------|
+|5 |
|$`a \ge b`$|one triangle exists|
+
+|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
+|:---|:----------------------------|:--------|:-----------------------------|
+|5 |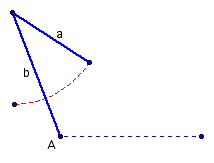 |$`a \le b`$|no triangle exists|
+|6 |
|$`a \le b`$|no triangle exists|
+|6 |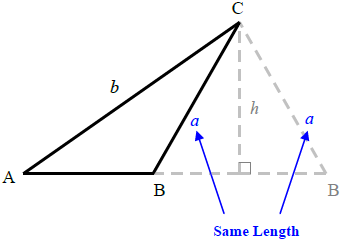 |$`a \gt b`$|one triangle exists|
+
+
+## Cosine Law
+
+In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
+
+**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
+
+## Directions
+
+`Bearins`: **Always** start from **North**, and goes **clockwise**
+`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
+
+**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
+
+## 2D Problems
+**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
+
+## 3D problems
+**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.
|$`a \gt b`$|one triangle exists|
+
+
+## Cosine Law
+
+In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
+
+**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
+
+## Directions
+
+`Bearins`: **Always** start from **North**, and goes **clockwise**
+`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
+
+**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
+
+## 2D Problems
+**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
+
+## 3D problems
+**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.
 +
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
+
+
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
+ +
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
+
+
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
+ +
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
@@ -83,10 +91,101 @@ our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and
Three pairs of corresponding sides are in the **same ratio**
+
+
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
@@ -83,10 +91,101 @@ our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and
Three pairs of corresponding sides are in the **same ratio**
+ +
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
+
+
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
+ +
### Angle-Angle similarity (AA $`\sim`$)
-Two pairs of corresponding angles are equal.
+Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
+
+
+
### Angle-Angle similarity (AA $`\sim`$)
-Two pairs of corresponding angles are equal.
+Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
+
+ +
+
+
+## Primary Trigonometry Ratios
+
+|Part Of Triangle|Property|
+|:---------------|:-------|
+|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
+|Opposite|The side opposite to the reference angle|
+|Adjacent|The side next to the reference agnle|
+
+**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
+
+### SOH CAH TOA
+
+**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
+
+**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
+
+**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
+
+## Angle Of Elevation And Depression
+
+| |Angle of Elevation|Angle of Depression|
+|:---------|:-----------------|:------------------|
+|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
+|Diagram|
+
+
+
+## Primary Trigonometry Ratios
+
+|Part Of Triangle|Property|
+|:---------------|:-------|
+|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
+|Opposite|The side opposite to the reference angle|
+|Adjacent|The side next to the reference agnle|
+
+**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
+
+### SOH CAH TOA
+
+**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
+
+**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
+
+**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
+
+## Angle Of Elevation And Depression
+
+| |Angle of Elevation|Angle of Depression|
+|:---------|:-----------------|:------------------|
+|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
+|Diagram| |
| |
+
+
+We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
+
+
|
+
+
+We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
+
+ +
+## Sine Law
+
+In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
+
+We can derive the formula further to get:
+- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
+- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
+- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
+
+Also, for some trigonometry identities:
+- $`\tan x = \dfrac{\sin x}{\cos x}`$
+- $`\sin^2 A + \cos^2 A = 1`$
+
+**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
+
+### Ambiguous Case
+The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
+
+In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
+
+
+|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
+|:---|:---------------------------|:--------|:-----------------------------|
+|1 |
+
+## Sine Law
+
+In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
+
+We can derive the formula further to get:
+- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
+- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
+- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
+
+Also, for some trigonometry identities:
+- $`\tan x = \dfrac{\sin x}{\cos x}`$
+- $`\sin^2 A + \cos^2 A = 1`$
+
+**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
+
+### Ambiguous Case
+The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
+
+In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
+
+
+|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
+|:---|:---------------------------|:--------|:-----------------------------|
+|1 | |$`a = h`$|one triangle exists|
+|3 |
|$`a = h`$|one triangle exists|
+|3 | |$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
+|4 |
|$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
+|4 | |$`a \ge b`$|one triangle exists|
+
+|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
+|:---|:----------------------------|:--------|:-----------------------------|
+|5 |
|$`a \ge b`$|one triangle exists|
+
+|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
+|:---|:----------------------------|:--------|:-----------------------------|
+|5 | |$`a \le b`$|no triangle exists|
+|6 |
|$`a \le b`$|no triangle exists|
+|6 | |$`a \gt b`$|one triangle exists|
+
+
+## Cosine Law
+
+In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
+
+**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
+
+## Directions
+
+`Bearins`: **Always** start from **North**, and goes **clockwise**
+`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
+
+**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
+
+## 2D Problems
+**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
+
+## 3D problems
+**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.
|$`a \gt b`$|one triangle exists|
+
+
+## Cosine Law
+
+In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
+
+**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
+
+## Directions
+
+`Bearins`: **Always** start from **North**, and goes **clockwise**
+`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
+
+**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
+
+## 2D Problems
+**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
+
+## 3D problems
+**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.