diff --git a/Grade 10/Math/MPM2DZ/Unit 1: Analytical Geometry.md b/Grade 10/Math/MPM2DZ/Unit 1: Analytical Geometry.md
index 766c575..338e10b 100644
--- a/Grade 10/Math/MPM2DZ/Unit 1: Analytical Geometry.md
+++ b/Grade 10/Math/MPM2DZ/Unit 1: Analytical Geometry.md
@@ -67,6 +67,8 @@ To get the center, just find a $`x, y`$ such that $`x - x_c = 0`$ and $`y - y_c
## Centroid
The centroid of a triangle is the common intersection of the 3 medians. The centroid is also known as the centre of mass or centre of gravity of an object (where the mass of an object is concentrated).
+ +
### Procedure To Determine The Centroid
1. Find the equation of the two median lines. **The median is the line segment from a vertex from a vertex to the midpoint of the opposite side**.
2. Find the point of intersection using elimnation or substitution.
@@ -77,14 +79,17 @@ centroid is simply at $`(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1+y_2+y_3}{3})`$
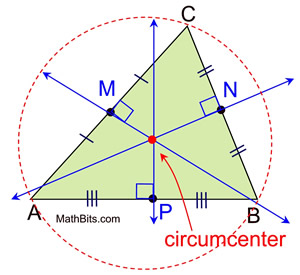
## Circumcentre
The circumcentre ($`O`$) of a triangle is the common intersection of the 3 perpendicular bisectors of the sides of a triangle.
+
+
### Procedure To Determine The Centroid
1. Find the equation of the two median lines. **The median is the line segment from a vertex from a vertex to the midpoint of the opposite side**.
2. Find the point of intersection using elimnation or substitution.
@@ -77,14 +79,17 @@ centroid is simply at $`(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1+y_2+y_3}{3})`$
## Circumcentre
The circumcentre ($`O`$) of a triangle is the common intersection of the 3 perpendicular bisectors of the sides of a triangle.
+ +
### Procedure To Determine The Centroid
1. Find the equation of the perpendicular bisectors of two sides. **A perpendicular (right) bisector is perpendicular to a side of the triangle and passes through the midpoint of that side of the triangle**.
2. Find the point of intersection of the two lines using elimination or substitution.
-
## Orthocentre
The orthocenter of a triangle is the common intersection of the 3 lines containing the altitudes.
+
+
### Procedure To Determine The Centroid
1. Find the equation of the perpendicular bisectors of two sides. **A perpendicular (right) bisector is perpendicular to a side of the triangle and passes through the midpoint of that side of the triangle**.
2. Find the point of intersection of the two lines using elimination or substitution.
-
## Orthocentre
The orthocenter of a triangle is the common intersection of the 3 lines containing the altitudes.
+ +
### Procedure To Determine The Orthocentre
1.Find the equation of two of the altitude lines. **An altitude is a perpendicular line segment from a vertex to the line of the opposite side.**
2. Find the point of intersection of the two lines using elimination or substitution.
+
### Procedure To Determine The Orthocentre
1.Find the equation of two of the altitude lines. **An altitude is a perpendicular line segment from a vertex to the line of the opposite side.**
2. Find the point of intersection of the two lines using elimination or substitution.
 +
### Procedure To Determine The Centroid
1. Find the equation of the two median lines. **The median is the line segment from a vertex from a vertex to the midpoint of the opposite side**.
2. Find the point of intersection using elimnation or substitution.
@@ -77,14 +79,17 @@ centroid is simply at $`(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1+y_2+y_3}{3})`$
## Circumcentre
The circumcentre ($`O`$) of a triangle is the common intersection of the 3 perpendicular bisectors of the sides of a triangle.
+
+
### Procedure To Determine The Centroid
1. Find the equation of the two median lines. **The median is the line segment from a vertex from a vertex to the midpoint of the opposite side**.
2. Find the point of intersection using elimnation or substitution.
@@ -77,14 +79,17 @@ centroid is simply at $`(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1+y_2+y_3}{3})`$
## Circumcentre
The circumcentre ($`O`$) of a triangle is the common intersection of the 3 perpendicular bisectors of the sides of a triangle.
+ +
### Procedure To Determine The Centroid
1. Find the equation of the perpendicular bisectors of two sides. **A perpendicular (right) bisector is perpendicular to a side of the triangle and passes through the midpoint of that side of the triangle**.
2. Find the point of intersection of the two lines using elimination or substitution.
-
## Orthocentre
The orthocenter of a triangle is the common intersection of the 3 lines containing the altitudes.
+
+
### Procedure To Determine The Centroid
1. Find the equation of the perpendicular bisectors of two sides. **A perpendicular (right) bisector is perpendicular to a side of the triangle and passes through the midpoint of that side of the triangle**.
2. Find the point of intersection of the two lines using elimination or substitution.
-
## Orthocentre
The orthocenter of a triangle is the common intersection of the 3 lines containing the altitudes.
+ +
### Procedure To Determine The Orthocentre
1.Find the equation of two of the altitude lines. **An altitude is a perpendicular line segment from a vertex to the line of the opposite side.**
2. Find the point of intersection of the two lines using elimination or substitution.
+
### Procedure To Determine The Orthocentre
1.Find the equation of two of the altitude lines. **An altitude is a perpendicular line segment from a vertex to the line of the opposite side.**
2. Find the point of intersection of the two lines using elimination or substitution.