# Unit 5: Analytical Geometry and Linear Relations
- ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
- ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
## Slope and Equation of Line
- ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```the rate of change```
- ```Slope Formula```: $`m = \dfrac{y_2 - y_1}{x_2 - x_1}`$
- ```Standard Form```: $`ax + by + c = 0, a \isin \mathbb{Z}, b \isin \mathbb{Z}, c \isin \mathbb{Z}`$ (must be integers and $`a`$ must be positive)
- ```Y-intercept Form```: $`y = mx + b`$
- ```Point-slope Form```: $`y_2-y_1 = m(x_2-x_1)`$
- The slope of a vertical lines is undefined
- The slope of a horizontal line is 0
- Parallel lines have the ```same slope```
- Perpendicular slopes are negative reciprocals
## Relations
- A relation can be described using
1. Table of Values (see below)
2. Equations $`(y = 3x + 5)`$
3. Graphs (Graphing the equation)
4. Words
- When digging into the earth, the temperature rises according to the
- following linear equation: $`t = 15 + 0.01 h`$. $`t`$ is the increase in temperature in
- degrees and $`h`$ is the depth in meters.
## Perpendicular Lines
- To find the perpendicular slope, you will need to find the slope point
- Formula: slope1 × slope2 = -1
- Notation: $`m_\perp`$
- 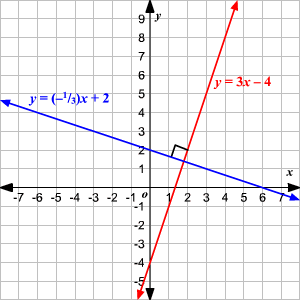 ## Definitions
- ```Parallel```: 2 lines with the same slope
- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
- ```Domain```: The **ordered** set of all possible values of the independent variable $`x`$.
- ```Range```: The **ordered** set of all possible values of the dependent variable $`y`$.
- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
- ```Collinear Points```: points that line on the same straight line
## Variables
- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
## Statistics
- ```Interpolation```: Data **inside** the given data set range.
- ```Extrapolation```: Data **outside** the data set range.
- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
- and it represents the trend of a graph.
- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
## Time - Distance Graph
- Time is the independent variable and distance is the dependent variable
- You can't go backwards on the x-axis, as you can't go back in time
- Plot the points accordingly
- Draw the lines accordingly
-
## Definitions
- ```Parallel```: 2 lines with the same slope
- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
- ```Domain```: The **ordered** set of all possible values of the independent variable $`x`$.
- ```Range```: The **ordered** set of all possible values of the dependent variable $`y`$.
- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
- ```Collinear Points```: points that line on the same straight line
## Variables
- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
## Statistics
- ```Interpolation```: Data **inside** the given data set range.
- ```Extrapolation```: Data **outside** the data set range.
- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
- and it represents the trend of a graph.
- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
## Time - Distance Graph
- Time is the independent variable and distance is the dependent variable
- You can't go backwards on the x-axis, as you can't go back in time
- Plot the points accordingly
- Draw the lines accordingly
- 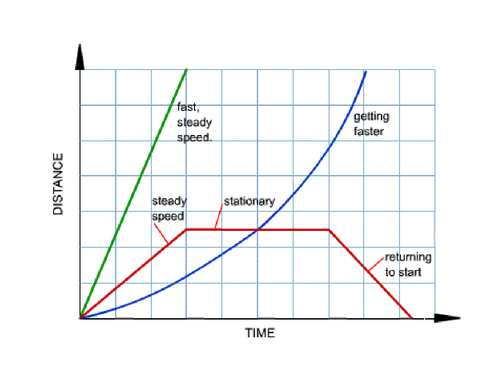 **Direction is always referring to:**
1. ```go towards home```
2. ```going away from home```
3. ```stop```
## Scatterplot and Line of Best Fit
- A scatterplot graph is there to show the relation between two variables in a table of values.
- A line of best fit is a straight line that describes the relation between two variables.
- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
-
**Direction is always referring to:**
1. ```go towards home```
2. ```going away from home```
3. ```stop```
## Scatterplot and Line of Best Fit
- A scatterplot graph is there to show the relation between two variables in a table of values.
- A line of best fit is a straight line that describes the relation between two variables.
- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
-  ### How To Determine the Equation Of a Line of Best Fit
1. Find two points **```ON```** the ```line of best fit```
2. Determine the ```slope``` using the two points
3. Use ```point-slope form``` to find the equation of the ```line of best fit```
## Table of values
- To find first differences or any points on the line, you can use a ```table of values```
| y | x |First Difference|
|:--|:--|:---------------|
|-1|-2|.....|
|0|-1|(-1)-(-2) = 1|
|1|0|0 - (-1) = 1|
|2|1|1 - 0 = 1|
|3|2|2 - 1 = 1|
|4|3|3 - 2 = 1|
## Tips
- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
- Draw your ```Line of Best Fit``` correctly
- Read the word problems carefully, and make sure you understand it when graphing things
- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
- Label your lines
### How To Determine the Equation Of a Line of Best Fit
1. Find two points **```ON```** the ```line of best fit```
2. Determine the ```slope``` using the two points
3. Use ```point-slope form``` to find the equation of the ```line of best fit```
## Table of values
- To find first differences or any points on the line, you can use a ```table of values```
| y | x |First Difference|
|:--|:--|:---------------|
|-1|-2|.....|
|0|-1|(-1)-(-2) = 1|
|1|0|0 - (-1) = 1|
|2|1|1 - 0 = 1|
|3|2|2 - 1 = 1|
|4|3|3 - 2 = 1|
## Tips
- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
- Draw your ```Line of Best Fit``` correctly
- Read the word problems carefully, and make sure you understand it when graphing things
- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
- Label your lines ## Definitions
- ```Parallel```: 2 lines with the same slope
- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
- ```Domain```: The **ordered** set of all possible values of the independent variable $`x`$.
- ```Range```: The **ordered** set of all possible values of the dependent variable $`y`$.
- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
- ```Collinear Points```: points that line on the same straight line
## Variables
- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
## Statistics
- ```Interpolation```: Data **inside** the given data set range.
- ```Extrapolation```: Data **outside** the data set range.
- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
- and it represents the trend of a graph.
- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
## Time - Distance Graph
- Time is the independent variable and distance is the dependent variable
- You can't go backwards on the x-axis, as you can't go back in time
- Plot the points accordingly
- Draw the lines accordingly
-
## Definitions
- ```Parallel```: 2 lines with the same slope
- ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
- ```Domain```: The **ordered** set of all possible values of the independent variable $`x`$.
- ```Range```: The **ordered** set of all possible values of the dependent variable $`y`$.
- ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
- ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
- ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
- ```Collinear Points```: points that line on the same straight line
## Variables
- ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
- ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
## Statistics
- ```Interpolation```: Data **inside** the given data set range.
- ```Extrapolation```: Data **outside** the data set range.
- ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
- and it represents the trend of a graph.
- ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
- ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
## Time - Distance Graph
- Time is the independent variable and distance is the dependent variable
- You can't go backwards on the x-axis, as you can't go back in time
- Plot the points accordingly
- Draw the lines accordingly
-  **Direction is always referring to:**
1. ```go towards home```
2. ```going away from home```
3. ```stop```
## Scatterplot and Line of Best Fit
- A scatterplot graph is there to show the relation between two variables in a table of values.
- A line of best fit is a straight line that describes the relation between two variables.
- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
-
**Direction is always referring to:**
1. ```go towards home```
2. ```going away from home```
3. ```stop```
## Scatterplot and Line of Best Fit
- A scatterplot graph is there to show the relation between two variables in a table of values.
- A line of best fit is a straight line that describes the relation between two variables.
- If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
-  ### How To Determine the Equation Of a Line of Best Fit
1. Find two points **```ON```** the ```line of best fit```
2. Determine the ```slope``` using the two points
3. Use ```point-slope form``` to find the equation of the ```line of best fit```
## Table of values
- To find first differences or any points on the line, you can use a ```table of values```
| y | x |First Difference|
|:--|:--|:---------------|
|-1|-2|.....|
|0|-1|(-1)-(-2) = 1|
|1|0|0 - (-1) = 1|
|2|1|1 - 0 = 1|
|3|2|2 - 1 = 1|
|4|3|3 - 2 = 1|
## Tips
- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
- Draw your ```Line of Best Fit``` correctly
- Read the word problems carefully, and make sure you understand it when graphing things
- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
- Label your lines
### How To Determine the Equation Of a Line of Best Fit
1. Find two points **```ON```** the ```line of best fit```
2. Determine the ```slope``` using the two points
3. Use ```point-slope form``` to find the equation of the ```line of best fit```
## Table of values
- To find first differences or any points on the line, you can use a ```table of values```
| y | x |First Difference|
|:--|:--|:---------------|
|-1|-2|.....|
|0|-1|(-1)-(-2) = 1|
|1|0|0 - (-1) = 1|
|2|1|1 - 0 = 1|
|3|2|2 - 1 = 1|
|4|3|3 - 2 = 1|
## Tips
- Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
- Draw your ```Line of Best Fit``` correctly
- Read the word problems carefully, and make sure you understand it when graphing things
- Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
- Label your lines