# Unit 4: Trigonometry
## Angle Theorems
1. ```Transversal Parallel Line Theorems``` (TPT)
a. Alternate Angles are Equal ```(Z-Pattern)```
b. Corresponding Angles Equal ```(F-Pattern)```
c. Interior Angles add up to 180 ```(C-Pattern)```
-  2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-
2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
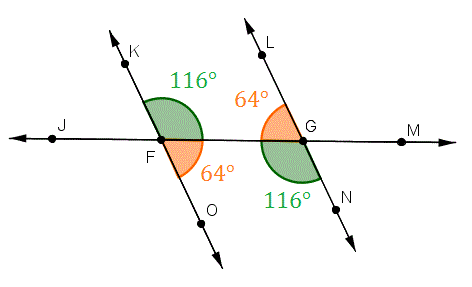
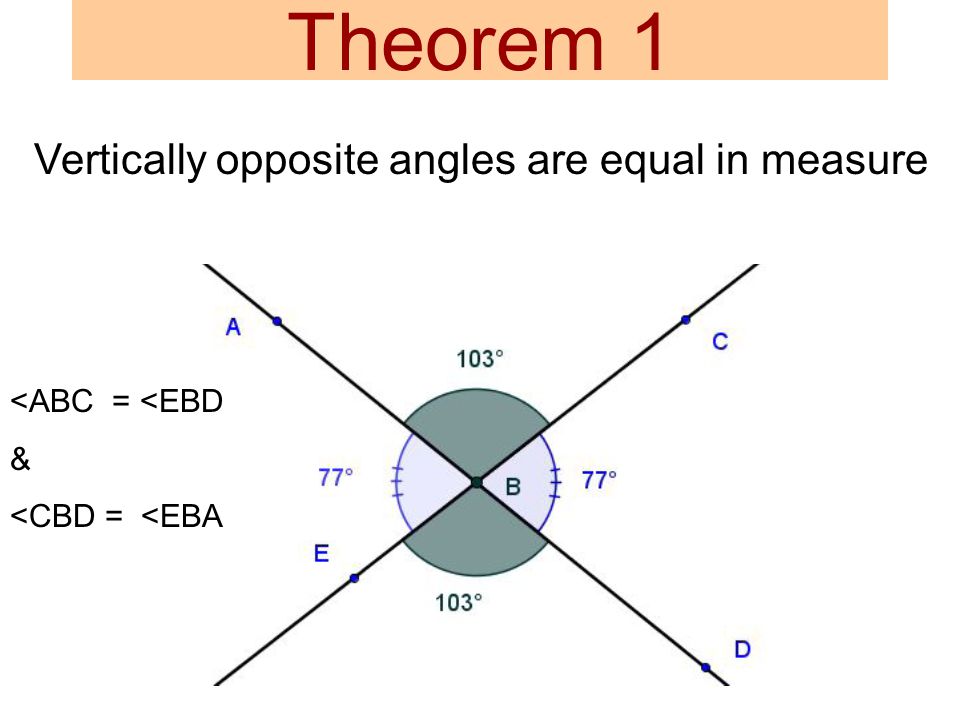
-  3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-
3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-  4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-
4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-  5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-
5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-  6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
- 7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-
7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-  8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-
8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-  9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-
9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-  ## Congruency
`Congruent`: Same size and shape
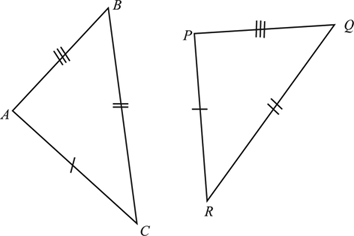
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
 ### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
 ### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
 ## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
 ### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
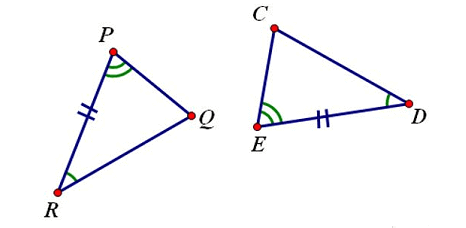
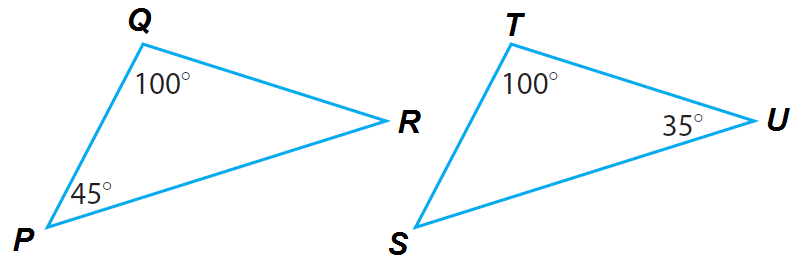
 ### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
 ## Primary Trigonometry Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram|
## Primary Trigonometry Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram| |
| |
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
|
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
 ## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 |
## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 | |$`a \lt h`$|no triangle exists|
|2 |
|$`a \lt h`$|no triangle exists|
|2 | |$`a = h`$|one triangle exists|
|3 |
|$`a = h`$|one triangle exists|
|3 |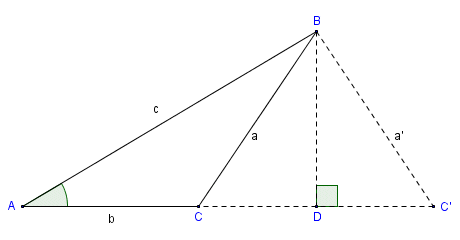 |$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 |
|$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 | |$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 |
|$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 | |$`a \le b`$|no triangle exists|
|6 |
|$`a \le b`$|no triangle exists|
|6 | |$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearins`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.
|$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearins`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.
 2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-
2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-  3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-
3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-  4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-
4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-  5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-
5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-  6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
- 7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-
7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-  8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-
8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-  9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-
9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-  ## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
 ### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
 ### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
 ## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
 ### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
 ## Primary Trigonometry Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram|
## Primary Trigonometry Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary Trigonometry ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram| |
| |
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
|
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
 ## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 |
## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle side side. The sine law calculation may need to 0, 1, or 2 solutions.
In the ambigouous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 | |$`a = h`$|one triangle exists|
|3 |
|$`a = h`$|one triangle exists|
|3 | |$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 |
|$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 | |$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 |
|$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 | |$`a \le b`$|no triangle exists|
|6 |
|$`a \le b`$|no triangle exists|
|6 | |$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearins`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.
|$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearins`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees to the second letter (N, E, S, W)
**Note:** Northeast, Southeast, NorthWest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats etc) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometry ratios whenever necessary.