# Math Study Sheet!!!!
# Essential Skills (1)
> ## Simple Arithmetics
>> ### Addition / Subtraction
>>> | Expression | Equivalent|
>>> |:----------:|:---------:|
>>> | a + b | a + b |
>>> | (-a) + b | b - a |
>>> | a + (-b) | a - b |
>>> | (-a) + (-b) | -(a + b) |
>>> | a - b | a - b|
>>> | a - (-b) | a + b |
>>> | (-a) -(-b) | (-a) + b|
>> ### Multiplication / Division
>>> | Signs | Outcome |
>>> |:-----:|:-------:|
>>> | a * b | Positive |
>>> | (-a) * b | Negative |
>>> | a * (-b) | Negative |
>>> | (-a) * (-b) | Positive |
>> ### BEDMAS / PEMDAS
>>> Follow ```BEDMAS``` for order of operations if there are more than one operation
>>> | Letter | Meaning |
>>> |:------:|:-------:|
>>> | B / P | Bracket / Parentheses |
>>> | E | Exponent |
>>> | D | Divison |
>>> | M | Multiplication |
>>> | A | Addition |
>>> | S | Subtraction |
>>>  > ## Interval Notation
>> A notation that represents an interval as a pair of numbers.
>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
>> ```|``` means ```such that```
>> ```E``` or ∈ means ```element of```
>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
>> | Symbol | Meaning |
>> |:------:|:-------:|
>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
>> | [a, b] | Inclusive |
>> | a ∪ b | Union (or) |
>> | a ∩ b | Intersection (and) |
> ## Pythgorean Theorem
>> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
>> a2 + b2 = c2
>>
> ## Interval Notation
>> A notation that represents an interval as a pair of numbers.
>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
>> ```|``` means ```such that```
>> ```E``` or ∈ means ```element of```
>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
>> | Symbol | Meaning |
>> |:------:|:-------:|
>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
>> | [a, b] | Inclusive |
>> | a ∪ b | Union (or) |
>> | a ∩ b | Intersection (and) |
> ## Pythgorean Theorem
>> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
>> a2 + b2 = c2
>>  > ## Operations with Rationals
>> Q = {
> ## Operations with Rationals
>> Q = {  | a, b ∈ Z, b ≠ 0 }
>>
>> Any operations with rationals, there are 2 sets of rules
>>> 1. ```Rules for operations with integers```
>>> 2. ```Rules for operations with fractions```
>> To Add / subtract rationals, find common denominator and then add / subtract numerator
>> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
>> To Divide rationals, multiply them by the reciprocal
>> ### Example Simplify Fully:
>>>
| a, b ∈ Z, b ≠ 0 }
>>
>> Any operations with rationals, there are 2 sets of rules
>>> 1. ```Rules for operations with integers```
>>> 2. ```Rules for operations with fractions```
>> To Add / subtract rationals, find common denominator and then add / subtract numerator
>> To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
>> To Divide rationals, multiply them by the reciprocal
>> ### Example Simplify Fully:
>>>  [Reduce to lowest terms]
>>>
[Reduce to lowest terms]
>>>  [Multiply by reciprocal]
>>>
[Multiply by reciprocal]
>>> >>>
>>>  [Leave as an improper fraction]
>> ### Shortcut for multiplying fractions
>>> cross divide to keep your numbers small
>>> Example:
>>>
[Leave as an improper fraction]
>> ### Shortcut for multiplying fractions
>>> cross divide to keep your numbers small
>>> Example:
>>>  >>>
>>>  >>>
>>>  >> ## Exponent Laws
>>> | Rule | Description| Example |
>>> |:----:|:----------:|:-------:|
>>> |Product|am × an = an+m|23 × 22 = 25|
>>> |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
>>> |Power of a Power|(am)n = amn|(23)2 = 26|
>>> |Power of a Quotient|
>> ## Exponent Laws
>>> | Rule | Description| Example |
>>> |:----:|:----------:|:-------:|
>>> |Product|am × an = an+m|23 × 22 = 25|
>>> |Quotient|am ÷ an = an-m|34 ÷ 32 = 32|
>>> |Power of a Power|(am)n = amn|(23)2 = 26|
>>> |Power of a Quotient| =
=  |
| =
=  |
>>> |Zero as Exponents|a0 = 1|210 = 1|
>>> |Negative Exponents|a-m =
|
>>> |Zero as Exponents|a0 = 1|210 = 1|
>>> |Negative Exponents|a-m =  |1-10 =
|1-10 =  |
>>> |Rational Exponents|an/m =
|
>>> |Rational Exponents|an/m =  |
| =
=  |
>>> **Note:**
>>> Exponential Form --> Expanded Form
>>> 64 = 6 × 6 × 6 × 6
>> ## Scientific Notation
>>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
>>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
>>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
>>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
>>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
>>>
|
>>> **Note:**
>>> Exponential Form --> Expanded Form
>>> 64 = 6 × 6 × 6 × 6
>> ## Scientific Notation
>>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
>>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
>>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
>>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
>>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
>>>  >> ## Rates, Ratio and Percent
>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
>>> Examples: ```a:b, a:b:c, a/b, a to b ```
>>> ```Rates```: A comparison of quantities expressed in different units.
>>> Example: ```10km/hour```
>>> ```Percent```: A fraction or ratio in which the denominator is 100
>>> Examples: ```50%, 240/100```
> ## Number Lines
>> a line that goes from a point to another point, a way to visualize set notations and the like
>>
>> ## Rates, Ratio and Percent
>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
>>> Examples: ```a:b, a:b:c, a/b, a to b ```
>>> ```Rates```: A comparison of quantities expressed in different units.
>>> Example: ```10km/hour```
>>> ```Percent```: A fraction or ratio in which the denominator is 100
>>> Examples: ```50%, 240/100```
> ## Number Lines
>> a line that goes from a point to another point, a way to visualize set notations and the like
>>  >> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
> ## Tips
>> Watch out for the ```+/-``` signs
>> Make sure to review your knowledge of the exponent laws
>> For scientific notation, watch out for the decimal point
>> Use shortcut when multiplying fractions
# Polyomials (2)
> ## Introduction to Polynomials
>> A ```variable``` is a letter that represents one or more numbers
>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
> ## Methods to solve a polynomial
>> 1. ```Combine like terms```
>> 2. ```Dividing polynomials```
>> 3. ```Multiplying polynomials```
> ## Simplifying Alegebraic Expressions
>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
> ## Factoring
>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
>> (e.g 5x + 10 = 5(x + 2) ).
>> |Type of Polynomial|Definition|
>> |:-----------------|:---------|
>> |Monomial|Polynomial that only has one term|
>> |Binomial|Polynomial that only has 2 terms|
>> |Trinomial|polynomial that only has 3 terms|
>> |Type|Example|
>> |:--:|:-----:|
>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
> ## Shortcuts
>>
>> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
> ## Tips
>> Watch out for the ```+/-``` signs
>> Make sure to review your knowledge of the exponent laws
>> For scientific notation, watch out for the decimal point
>> Use shortcut when multiplying fractions
# Polyomials (2)
> ## Introduction to Polynomials
>> A ```variable``` is a letter that represents one or more numbers
>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
> ## Methods to solve a polynomial
>> 1. ```Combine like terms```
>> 2. ```Dividing polynomials```
>> 3. ```Multiplying polynomials```
> ## Simplifying Alegebraic Expressions
>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
> ## Factoring
>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
>> (e.g 5x + 10 = 5(x + 2) ).
>> |Type of Polynomial|Definition|
>> |:-----------------|:---------|
>> |Monomial|Polynomial that only has one term|
>> |Binomial|Polynomial that only has 2 terms|
>> |Trinomial|polynomial that only has 3 terms|
>> |Type|Example|
>> |:--:|:-----:|
>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
> ## Shortcuts
>>  > ## Foil / Rainbow Method
>>
> ## Foil / Rainbow Method
>> 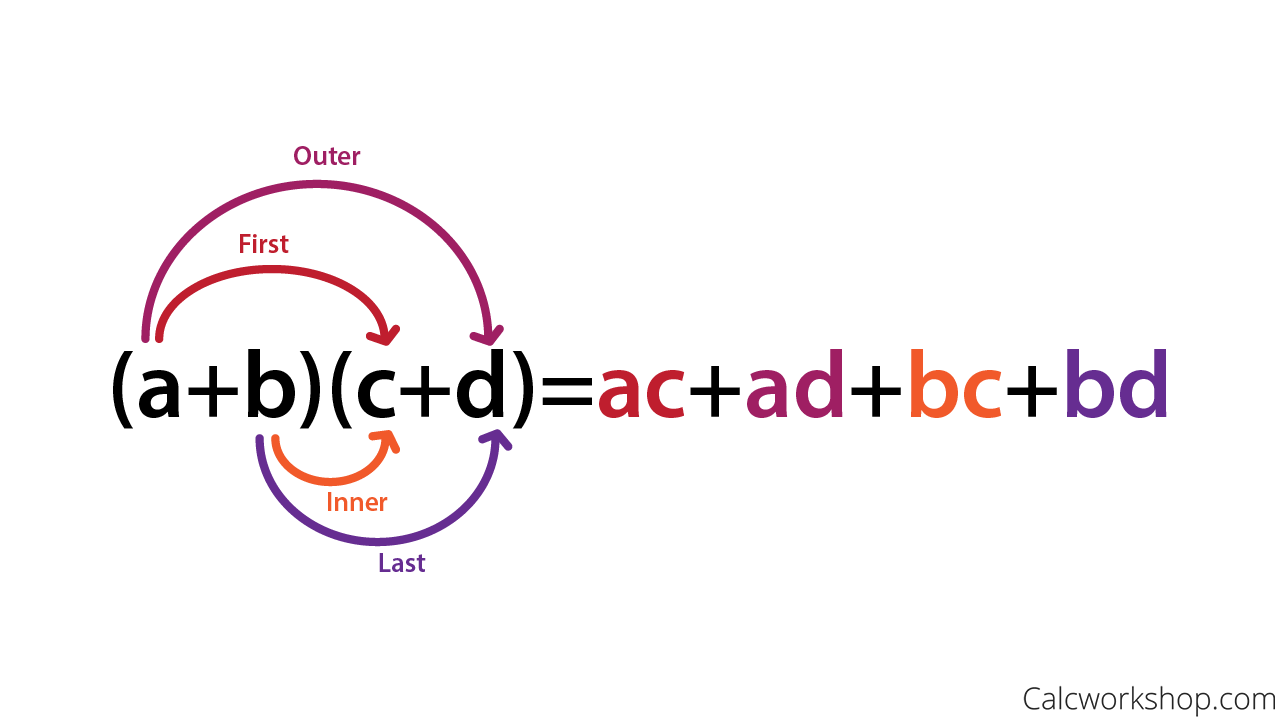 > ## Definitions
>> ```Term``` a variable that may have coefficient(s) or a constant
>> ```Alebraic Expressions```: made up of one or more terms
>> ```Like-terms```: same variables raised to the same exponent
> ## Tips
>> Be sure to factor fully
>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
>> Remember your formulas
>> Simplify first, combine like terms
# Solving Equations and Inequailties (3)
> ## Equations
>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
>> To ```solve``` and equation is to find the variable that makes the statement true
>> ### Methods to solve an equation
>>> 1. Expand and simplify both sides
>>> 2. Isolate using reverse order of operations
>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
>
> ## Absolute Values
>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
>> equations will have the absolute bracket be positive while the other negative.
>> Absolute values are written in the form ```| x |```
>> where
>> if x > 0, | x | = x
>> if x = 0, | x | = 0
>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
>> Solve quadratic equation by:
>> 1. Isolation
>> a(x+b)2 + k = 0
>> 2. Factor using zero-product property
>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
>> (x-a)(x-b)=0
>> x = a, b
>>
> ## Definitions
>> ```Term``` a variable that may have coefficient(s) or a constant
>> ```Alebraic Expressions```: made up of one or more terms
>> ```Like-terms```: same variables raised to the same exponent
> ## Tips
>> Be sure to factor fully
>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
>> Remember your formulas
>> Simplify first, combine like terms
# Solving Equations and Inequailties (3)
> ## Equations
>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
>> To ```solve``` and equation is to find the variable that makes the statement true
>> ### Methods to solve an equation
>>> 1. Expand and simplify both sides
>>> 2. Isolate using reverse order of operations
>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
>
> ## Absolute Values
>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
>> equations will have the absolute bracket be positive while the other negative.
>> Absolute values are written in the form ```| x |```
>> where
>> if x > 0, | x | = x
>> if x = 0, | x | = 0
>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
>> Solve quadratic equation by:
>> 1. Isolation
>> a(x+b)2 + k = 0
>> 2. Factor using zero-product property
>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
>> (x-a)(x-b)=0
>> x = a, b
>>  >> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
> ## Tips
>> ```Absolute Values``` can have 2 solutions
>> ```Quadratics``` can also have 2 solutions
>> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
# Measurement and Geometry (4)
> ## Angle Theorems
> 1. ```Transversal Parallel Line Theorems``` (TPT)
> a. Alternate Angles are Equal ```(Z-Pattern)```
> b. Corresponding Angles Equal ```(F-Pattern)```
> c. Interior Angles add up to 180 ```(C-Pattern)```
>
>> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
> ## Tips
>> ```Absolute Values``` can have 2 solutions
>> ```Quadratics``` can also have 2 solutions
>> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
# Measurement and Geometry (4)
> ## Angle Theorems
> 1. ```Transversal Parallel Line Theorems``` (TPT)
> a. Alternate Angles are Equal ```(Z-Pattern)```
> b. Corresponding Angles Equal ```(F-Pattern)```
> c. Interior Angles add up to 180 ```(C-Pattern)```
>  > 2. ```Supplementary Angle Triangle``` (SAT)
> - When two angles add up to 180 degrees
>
> 2. ```Supplementary Angle Triangle``` (SAT)
> - When two angles add up to 180 degrees
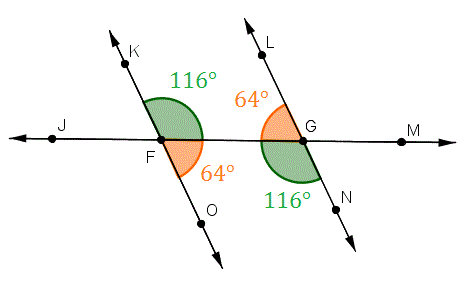
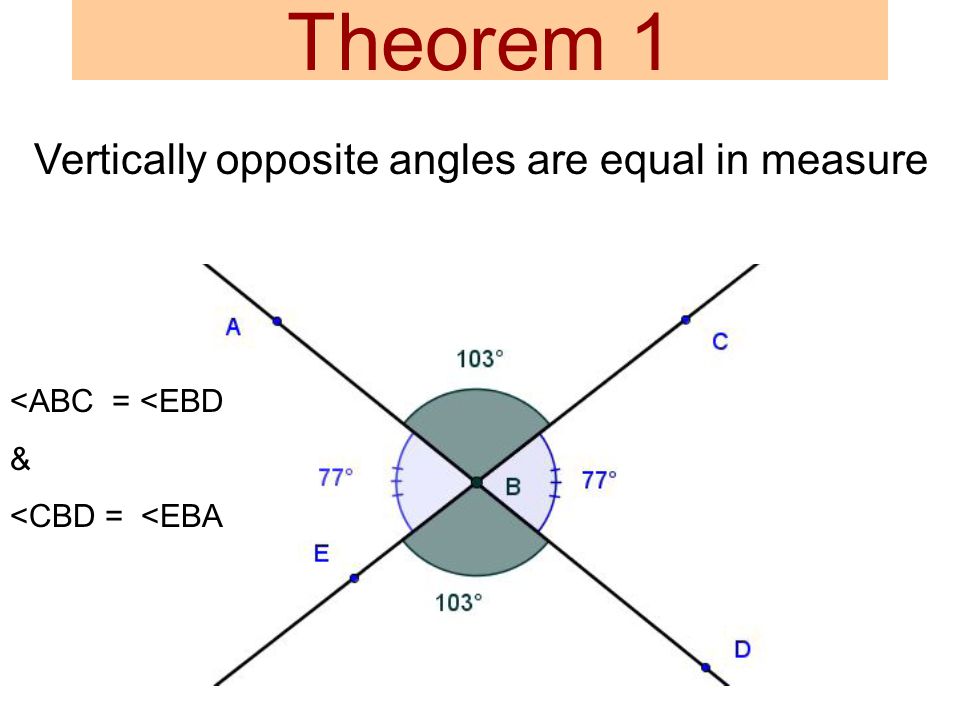
>  > 3. ```Opposite Angle Theorem (OAT)``` (OAT)
> - Two lines intersect, two angles form opposite. They have equal measures
>
> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
> - Two lines intersect, two angles form opposite. They have equal measures
>  > 4. ```Complementary Angle Theorem``` (CAT)
> - The sum of two angles that add up to 90 degrees
>
> 4. ```Complementary Angle Theorem``` (CAT)
> - The sum of two angles that add up to 90 degrees
>  > 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
> - The sum of the three interior angles of any triangle is 180 degrees
>
> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
> - The sum of the three interior angles of any triangle is 180 degrees
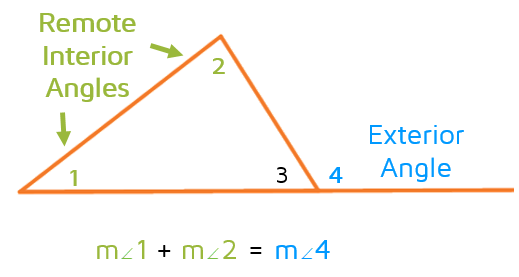
>  > 6. ```Exterior Angle Theorem``` (EAT)
> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
>
> 6. ```Exterior Angle Theorem``` (EAT)
> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
>  > 7. ``` Isosceles Triangle Theorem``` (ITT)
> - The base angles in any isosceles triangle are equal
>
> 7. ``` Isosceles Triangle Theorem``` (ITT)
> - The base angles in any isosceles triangle are equal
> 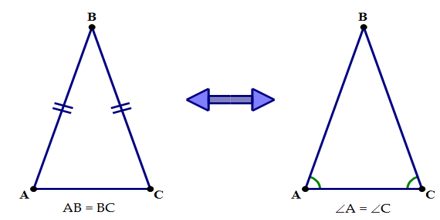 > 8. ```Sum of The Interior Angle of a Polygon```
> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
> 8. ```Sum of The Interior Angle of a Polygon```
> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
 > 9. ```Exterior Angles of a Convex Polygon```
> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
> 9. ```Exterior Angles of a Convex Polygon```
> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
 > ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
>> |Figure|Properties|
>> |:-----|:---------|
>> |Scalene Triangle|no sides equal|Length of line segment|
>> |Isosceles Triangle| two sides equal|Length of line segment|
>> |Equilateral Triangle|All sides equal|Length of line segment|
>> |Right Angle Triangle|Two sides are perpendicular to each other|
>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
>> |Kite|The diagonals are perpendicular|
> ## 2D Geometry Equations
>> |Shape|Formula|Picture|
>> |:----|:------|:------|
>> |Rectangle|```Area```: lw
> ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
>> |Figure|Properties|
>> |:-----|:---------|
>> |Scalene Triangle|no sides equal|Length of line segment|
>> |Isosceles Triangle| two sides equal|Length of line segment|
>> |Equilateral Triangle|All sides equal|Length of line segment|
>> |Right Angle Triangle|Two sides are perpendicular to each other|
>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
>> |Kite|The diagonals are perpendicular|
> ## 2D Geometry Equations
>> |Shape|Formula|Picture|
>> |:----|:------|:------|
>> |Rectangle|```Area```: lw
```Perimeter```: 2(l+w)| |
>> |Triangle|```Area```: bh/2
|
>> |Triangle|```Area```: bh/2
```Perimeter```: a+b+c| |
>> |Circle|```Area```: πr2
|
>> |Circle|```Area```: πr2
```Circumference```: 2πr or πd| |
>> |Trapezoid|```Area```: (a+b)h/2
|
>> |Trapezoid|```Area```: (a+b)h/2
```Perimeter```: a+b+c+d| |
> ## 3D Geometry Equations
>> |3D Object|Formula|Picture|
>> |:----|:------|:------|
>> |Rectangular Prism|```Volume```: lwh
|
> ## 3D Geometry Equations
>> |3D Object|Formula|Picture|
>> |:----|:------|:------|
>> |Rectangular Prism|```Volume```: lwh
```SA```: 2(lw+lh+wh)| |
>> |Square Based Pyramid|```Volume```: 1⁄3b2h
|
>> |Square Based Pyramid|```Volume```: 1⁄3b2h
```SA```: 2bs+b2| |
>> |Sphere|```Volume```: 4⁄3πr3
|
>> |Sphere|```Volume```: 4⁄3πr3
```SA```: 4πr2| |
>> |Cone|```Volume```: 1⁄3πr2h
|
>> |Cone|```Volume```: 1⁄3πr2h
```SA```: πrs+πr2| |
>> |Cylinder|```Volume```: πr2h
|
>> |Cylinder|```Volume```: πr2h
```SA```: 2πr2+2πh| |
>> |Triangular Prism|```Volume```: ah+bh+ch+bl
|
>> |Triangular Prism|```Volume```: ah+bh+ch+bl
```SA```: 1⁄2blh| |
> ## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
>> ### 2D Objects
>> |Shape|Maximum Area|Minimum Perimeter|
>> |:----|:-----------|:----------------|
>> |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
|
> ## Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
>> ### 2D Objects
>> |Shape|Maximum Area|Minimum Perimeter|
>> |:----|:-----------|:----------------|
>> |4-sided rectangle|A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width
A = lw
Amax = (w)(w)
Amax = w2|A rectangle must be a square to minimaze the perimeter for a given area. The length is equal to the width.
P = 2(l+w)
Pmin = 2(w)(w)
Pmin = 2(2w)
Pmin = 4w|
>> |3-sided rectangle|l = 2w
A = lw
Amax = 2w(w)
Amax = 2w2|l = 2w
P = l+w2
Pmin = 2w+2w
Pmin = 4w|
>> ### 3D Objects
>> |3D Object|Maximum Volumne|Minimum Surface Area|
>> |:--------|:--------------|:-------------------|
>> |Cylinder(closed-top)|The cylinder must be similar to a cube where h = 2r
V = πr2h
Vmax = πr2(2r)
Vmax = 2πr2|The cylinder must be similar to a cube where h = 2r
SA = 2πr2+2πrh
SAmin = 2πr2+2πr(2r)
SAmin = 2πr2+4πr2
SAmin = 6πr2|
>> |Rectangular Prism(closed-top)|The prism must be a cube,
where l = w = h
V = lwh
Vmax = (w)(w)(w)
Vmax = w3|The prism must be a cube,
where l = w = h
SA = 2lh+2lw+2wh
SAmin = 2w2+2w2+2w2
SAmin = 6w2|
>> |Cylinder(open-top)|h = r
V = πr2h
Vmax = πr2(r)
Vmax = πr3|h = r
SA = πr2+2πrh
SAmin = πr2+2πr(r)
SAmin = πr2+2πr2
SAmin = 3πr2|
>> |Square-Based Rectangular Prism(open-top)|h = w/2
V = lwh
Vmax = (w)(w)(w⁄2)
Vmax = w3⁄2|h = w/2
SA = w2+4wh
SAmin = w2+4w(w⁄2)
SAmin = w2+2w2
SAmin = 3w2|
> ## Labelling
>> Given any polygons, labelling the vertices must always:
>> 1. use ```CAPITAL LETTERS```
>> 2. they have to be labeled in ```clockwise``` or ```counter-clockwise``` directions
>> For a triangle, the side lengths are labeled in ```LOWERCASE LETTERS``` associated to the opposite side of the vertex
>> 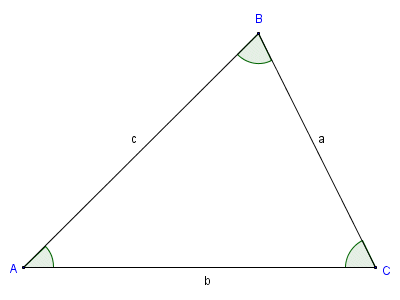 > ## Median
>> Each median divides the triangle into 2 smaller triangles of equal area
>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
>>
> ## Median
>> Each median divides the triangle into 2 smaller triangles of equal area
>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
>>  > ## Terms:
>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
>>>
> ## Terms:
>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
>>> 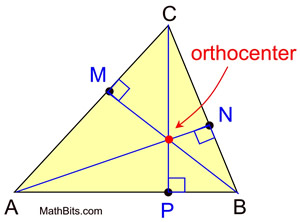 >> ```Midpoint```: A point on a line where the length of either side of the point are equal
>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
>> ```Centroid```: The intersection of the 3 medians of a triangle
>>>
>> ```Midpoint```: A point on a line where the length of either side of the point are equal
>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
>> ```Centroid```: The intersection of the 3 medians of a triangle
>>>  > ## Proportionality theorem:
>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
>>
> ## Proportionality theorem:
>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
>>  > ## Tips
>> Make sure to know your optimization formualas
>> Read the word problems carefully, determine which formual to use
>> Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
>> To find ```missing area```, take what you have, subtract what you don't want
>> Don't be afraid to draw lines to help you solve the problem
# Analytical Geometry and Linear Relations (5)
> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
> ## Slope and Equation of Line
>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```rate of change y / rate of change x```
>> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
>> ```Y-intercept Form```: **y = mx + b**
>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
>> The slope of a vertical lines is undefined
>> The sloope of a horizontal line is 0
>> Parallel lines have the ```same slope```
>> Perpendicular slopes are negative reciprocals
> ## Relations
>> A relation can be described using
>> 1. Table of Values (see below)
>> 2. Equations (y = 3x + 5)
>> 3. Graphs (Graphing the equation)
>> 4. Words
>> When digging into the earth, the temperature rises according to the
>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
>> degrees and **h** is the depth in meters.
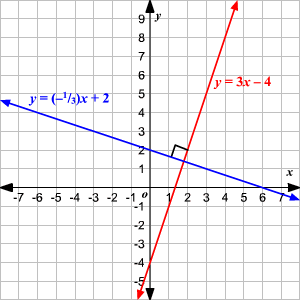
> ## Perpendicular Lines
>> To find the perpendicular slope, you will need to find the slope point
>> Formula: slope1 × slope2 = -1
>> Notation: m⊥
>>
> ## Tips
>> Make sure to know your optimization formualas
>> Read the word problems carefully, determine which formual to use
>> Never **ASSUME**, be sure to **CALCULATE** as most of the time the drawings are **NOT ACCURATE**
>> To find ```missing area```, take what you have, subtract what you don't want
>> Don't be afraid to draw lines to help you solve the problem
# Analytical Geometry and Linear Relations (5)
> ```Linear Relation```: A relation which a single straight line can be drawn through every data point and the first differences are constant
> ```Non - Linear Relation```: A single smooth curve can be drawn through every data point and the first differences are not constant
> ## Slope and Equation of Line
>> ```Slope```: The measure of the steepness of a line - ```rise / run``` or ```rate of change y / rate of change x```
>> ```Slope Formula```: **m = (y2-y1)/(x2-x1)**
>> ```Standard Form```: **ax + by + c = 0**, a∈Z, b∈Z, c∈Z (must be integers and ```a``` must be positive)
>> ```Y-intercept Form```: **y = mx + b**
>> ```Point-slope Form```: **y2-y1 = m(x2-x1)**
>> The slope of a vertical lines is undefined
>> The sloope of a horizontal line is 0
>> Parallel lines have the ```same slope```
>> Perpendicular slopes are negative reciprocals
> ## Relations
>> A relation can be described using
>> 1. Table of Values (see below)
>> 2. Equations (y = 3x + 5)
>> 3. Graphs (Graphing the equation)
>> 4. Words
>> When digging into the earth, the temperature rises according to the
>> following linear equation: t = 15 + 0.01 h. **t** is the increase in temperature in
>> degrees and **h** is the depth in meters.
> ## Perpendicular Lines
>> To find the perpendicular slope, you will need to find the slope point
>> Formula: slope1 × slope2 = -1
>> Notation: m⊥
>>  > ## Definitions
>> ```Parallel```: 2 lines with the same slope
>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
>> ```Collinear Points```: points that line on the same straight line
> ## Variables
>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
> ## Statistics
>> ```Interpolation```: Data **inside** the given data set range.
>> ```Extrapolation```: Data **outside** the data set range.
>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
>> and it represents the trend of a graph.
>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
> ## Time - Distance Graph
>> Time is the independent variable and distance is the dependent variable
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
>>
> ## Definitions
>> ```Parallel```: 2 lines with the same slope
>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
>> ```Collinear Points```: points that line on the same straight line
> ## Variables
>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
> ## Statistics
>> ```Interpolation```: Data **inside** the given data set range.
>> ```Extrapolation```: Data **outside** the data set range.
>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
>> and it represents the trend of a graph.
>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
> ## Time - Distance Graph
>> Time is the independent variable and distance is the dependent variable
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
>> 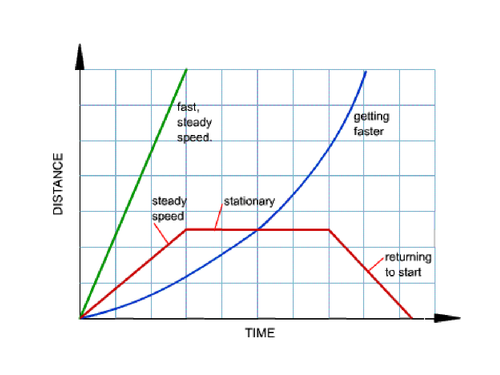 >> **Direction is always referring to:**
>> 1. ```go towards home```
>> 2. ```going away from home```
>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
>>
>> **Direction is always referring to:**
>> 1. ```go towards home```
>> 2. ```going away from home```
>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
>>  >> ### How To Determine the Equation Of a Line of Best Fit
>> 1. Find two points **```ON```** the ```line of best fit```
>> 2. Determine the ```slope``` using the two points
>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
>>| y | x |First Difference|
>>|:--|:--|:---------------|
>>|-1|-2|1|
>>|0|-1|1|
>>|1|0|1|
>>|2|1|1|
>>|3|2|1|
>>|4|3|1|
> ## Tips
>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
>> Draw your ```Line of Best Fit``` correctly
>> Read the word problems carefully, and make sure you understand it when graphing things
>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
>> Label your lines
# System of Equations (6)
> ## Linear System
>> Two or more equation that you are working on all together at once on the same set of axes.
>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
>> when **Profit = 0**. There is no gain or loss.
>> ### Number of Solutions
>>>
>> ### How To Determine the Equation Of a Line of Best Fit
>> 1. Find two points **```ON```** the ```line of best fit```
>> 2. Determine the ```slope``` using the two points
>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
>>| y | x |First Difference|
>>|:--|:--|:---------------|
>>|-1|-2|1|
>>|0|-1|1|
>>|1|0|1|
>>|2|1|1|
>>|3|2|1|
>>|4|3|1|
> ## Tips
>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
>> Draw your ```Line of Best Fit``` correctly
>> Read the word problems carefully, and make sure you understand it when graphing things
>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
>> Label your lines
# System of Equations (6)
> ## Linear System
>> Two or more equation that you are working on all together at once on the same set of axes.
>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
>> when **Profit = 0**. There is no gain or loss.
>> ### Number of Solutions
>>>  > ## Discriminant
>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
>> D = b2 - 4ac
>> D > 0 ```(2 distinct real solutions)```
>> D = 0 ```(1 real solution)```
>> D < 0 ```(no real solutions)```
>>
> ## Discriminant
>> The discriminant determines the number of solutions (roots) there are in a quadratic equation. ```a```, ```b```, ```c``` are the
>> coefficients and constant of a quadratic equation: ```y = ax2 + bx + c```
>> D = b2 - 4ac
>> D > 0 ```(2 distinct real solutions)```
>> D = 0 ```(1 real solution)```
>> D < 0 ```(no real solutions)```
>>  > ## Solving Linear-Quadratic Systems
>> To find the point of intersection, do the following:
>> 1. Isolate both equations for ```y```
>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
>> 3. Simplify and put everything on one side and equal to zero on the other side
>> 4. Factor
>> 5. Use zero-product property to solve for all possible x-values
>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
>> 7. State a conclusion / the solution
>>
> ## Solving Linear-Quadratic Systems
>> To find the point of intersection, do the following:
>> 1. Isolate both equations for ```y```
>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
>> 3. Simplify and put everything on one side and equal to zero on the other side
>> 4. Factor
>> 5. Use zero-product property to solve for all possible x-values
>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
>> 7. State a conclusion / the solution
>>  >> There are 3 possible cases
>> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
> # Ways to solve Systems of Equations
> 1. Subsitution
> Here we eliminate a variable by subbing in another variable from another equation
> We usually do this method if a variable is easily isolated
> Example:
> - ```
> y = x + 10 (1)
> x + y + 34 = 40 (2)
> ```
> We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
> ```x + (x + 10) + 34 = 40```
> ```2x + 44 = 40```
> ```2x = -4```
> ```x = -2```
> Then solve for ```y```
> ```y = -2 + 10```
> ```y = -8```
> 2. Elimination
> Here we eliminate a variable by basically eliminate a variable from an equation
> We usually use this method first when the variables are not easily isolated, then use subsitution to solve
> Example:
> - ```
> 2x + 3y = 10 (1)
> 4x + 3y = 14 (2)
> ```
> We can then use elimination
> ```
> 4x + 3y = 14
> 2x + 3y = 10
> ------------
> 2x + 0 = 4
> x = 2
> ```
> Then sub the value of ```x``` into an original equation and solve for ```y```
> ```2(2) + 3y = 10```
> ```3y = 6```
> ```y = 2```
> 3. Graphing
> we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
> ## Solving Systems of Linear Inequalities
>> Find the intersection region as the ```solution```.
>> ## If:
>> | |Use ```Dash``` line|Use ```Solid line```|
>> |:-|:------------------|:-------------------|
>> |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
>> |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
>> ## If
>> |x > a
>> There are 3 possible cases
>> In addition, to determine the number of solutions, you the Discriminant formula **D = b2 - 4ac**
> # Ways to solve Systems of Equations
> 1. Subsitution
> Here we eliminate a variable by subbing in another variable from another equation
> We usually do this method if a variable is easily isolated
> Example:
> - ```
> y = x + 10 (1)
> x + y + 34 = 40 (2)
> ```
> We can sub (1) into (2) to find ```x```, then you the value of ```x``` we found to solve for ```y```
> ```x + (x + 10) + 34 = 40```
> ```2x + 44 = 40```
> ```2x = -4```
> ```x = -2```
> Then solve for ```y```
> ```y = -2 + 10```
> ```y = -8```
> 2. Elimination
> Here we eliminate a variable by basically eliminate a variable from an equation
> We usually use this method first when the variables are not easily isolated, then use subsitution to solve
> Example:
> - ```
> 2x + 3y = 10 (1)
> 4x + 3y = 14 (2)
> ```
> We can then use elimination
> ```
> 4x + 3y = 14
> 2x + 3y = 10
> ------------
> 2x + 0 = 4
> x = 2
> ```
> Then sub the value of ```x``` into an original equation and solve for ```y```
> ```2(2) + 3y = 10```
> ```3y = 6```
> ```y = 2```
> 3. Graphing
> we can rewrite the equations into ```y-intercept form``` and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution
> ## Solving Systems of Linear Inequalities
>> Find the intersection region as the ```solution```.
>> ## If:
>> | |Use ```Dash``` line|Use ```Solid line```|
>> |:-|:------------------|:-------------------|
>> |Shade the region ```above``` the line|y > mx + b|y ≥ mx + b|
>> |Shade the region ```below``` the line|y < mx + b| y ≤ mx + b|
>> ## If
>> |x > a
x ≥ a|
>> |:------------------|
>> shade the region on the **right**
>> ## If
>> |x < a
x ≤ a|
>> |:------------------|
>> shade the region on the **left**
>> Step 1. change all inequalities to ```y-intercept form```
>> Step 2. graph the line
>> Step 3. shade the region where all the regions overlap
>> 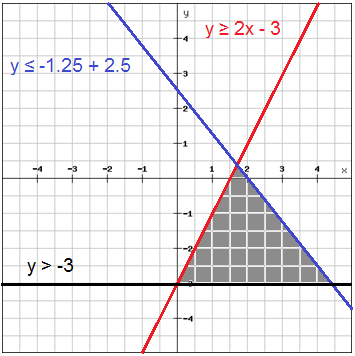 > ## Tips
>> Read the questions carefully and model the system of equations correctly
>> Be sure to name your equations
>> Label your lines
# General Tips
> Be sure to watch out for units, like ```cm``` or ```km```
> Watch out for ```+/-```
> Be sure to reverse the operation when moving things to the other side of the equation
> Make sure to have a proper scale for graphs
> Read question carefully and use the appropriate tools to solve
> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
> ## Word Problems
>> Read carefully
>> model equations correctly
>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
> ## Graph Problems
>> Look up on tips in units (5) and (6)
>> be sure to use a ruler when graphing
> ## System of Equations
>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
> Ryan Mark - He helped provide alot of information for me
> Magicalsoup - ME!
> ## Tips
>> Read the questions carefully and model the system of equations correctly
>> Be sure to name your equations
>> Label your lines
# General Tips
> Be sure to watch out for units, like ```cm``` or ```km```
> Watch out for ```+/-```
> Be sure to reverse the operation when moving things to the other side of the equation
> Make sure to have a proper scale for graphs
> Read question carefully and use the appropriate tools to solve
> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
> ## Word Problems
>> Read carefully
>> model equations correctly
>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
> ## Graph Problems
>> Look up on tips in units (5) and (6)
>> be sure to use a ruler when graphing
> ## System of Equations
>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
> Ryan Mark - He helped provide alot of information for me
> Magicalsoup - ME!
 > ## Interval Notation
>> A notation that represents an interval as a pair of numbers.
>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
>> ```|``` means ```such that```
>> ```E``` or ∈ means ```element of```
>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
>> | Symbol | Meaning |
>> |:------:|:-------:|
>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
>> | [a, b] | Inclusive |
>> | a ∪ b | Union (or) |
>> | a ∩ b | Intersection (and) |
> ## Pythgorean Theorem
>> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
>> a2 + b2 = c2
>>
> ## Interval Notation
>> A notation that represents an interval as a pair of numbers.
>> The numbers in the interval represent the endpoint. E.g. **[x > 3, x ∈ R]**
>> ```|``` means ```such that```
>> ```E``` or ∈ means ```element of```
>> ```W``` represents **Whole Numbers** (W = {x | x > 0, x ∈ Z})
>> ```N``` represents **Natural Numbers** (N = {x | x ≥ 0, x ∈ Z})
>> ```Z``` represents **Integers** (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
>> ```Q``` represents **Rational Numbers (Q = {a⁄b |a, b ∈ Z, b ≠ 0})
>> | Symbol | Meaning |
>> |:------:|:-------:|
>> | (a, b) | Between but not including ```a``` or ```b```, you also use this for ```∞``` |
>> | [a, b] | Inclusive |
>> | a ∪ b | Union (or) |
>> | a ∩ b | Intersection (and) |
> ## Pythgorean Theorem
>> a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
>> a2 + b2 = c2
>>  |
| |
>>> **Note:**
>>> Exponential Form --> Expanded Form
>>> 64 = 6 × 6 × 6 × 6
>> ## Scientific Notation
>>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
>>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
>>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
>>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
>>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
>>>
|
>>> **Note:**
>>> Exponential Form --> Expanded Form
>>> 64 = 6 × 6 × 6 × 6
>> ## Scientific Notation
>>> They convey accuracy and precision. It can either be written as its original number or in scientific notation:
>>> 555 (**Exact**) or 5.55 x 102 (**3 significant figures**).
>>> In scientific notation, values are written in the form **a(10n)**, where ```a``` is a number within 1 and 10 and ```n``` is any integer.
>>> Some examples include the following: 5.4 x 103, 3.0 x 102, and 4.56 x 10-4.
>>> When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used
>>>  >> ## Rates, Ratio and Percent
>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
>>> Examples: ```a:b, a:b:c, a/b, a to b ```
>>> ```Rates```: A comparison of quantities expressed in different units.
>>> Example: ```10km/hour```
>>> ```Percent```: A fraction or ratio in which the denominator is 100
>>> Examples: ```50%, 240/100```
> ## Number Lines
>> a line that goes from a point to another point, a way to visualize set notations and the like
>>
>> ## Rates, Ratio and Percent
>>> ```Ratio```: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
>>> Examples: ```a:b, a:b:c, a/b, a to b ```
>>> ```Rates```: A comparison of quantities expressed in different units.
>>> Example: ```10km/hour```
>>> ```Percent```: A fraction or ratio in which the denominator is 100
>>> Examples: ```50%, 240/100```
> ## Number Lines
>> a line that goes from a point to another point, a way to visualize set notations and the like
>>  >> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
> ## Tips
>> Watch out for the ```+/-``` signs
>> Make sure to review your knowledge of the exponent laws
>> For scientific notation, watch out for the decimal point
>> Use shortcut when multiplying fractions
# Polyomials (2)
> ## Introduction to Polynomials
>> A ```variable``` is a letter that represents one or more numbers
>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
> ## Methods to solve a polynomial
>> 1. ```Combine like terms```
>> 2. ```Dividing polynomials```
>> 3. ```Multiplying polynomials```
> ## Simplifying Alegebraic Expressions
>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
> ## Factoring
>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
>> (e.g 5x + 10 = 5(x + 2) ).
>> |Type of Polynomial|Definition|
>> |:-----------------|:---------|
>> |Monomial|Polynomial that only has one term|
>> |Binomial|Polynomial that only has 2 terms|
>> |Trinomial|polynomial that only has 3 terms|
>> |Type|Example|
>> |:--:|:-----:|
>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
> ## Shortcuts
>>
>> A solid filled dot is used for ```[]``` and a empty dot is used for ```()```
> ## Tips
>> Watch out for the ```+/-``` signs
>> Make sure to review your knowledge of the exponent laws
>> For scientific notation, watch out for the decimal point
>> Use shortcut when multiplying fractions
# Polyomials (2)
> ## Introduction to Polynomials
>> A ```variable``` is a letter that represents one or more numbers
>> An ```algebraic expression``` is a combination of variables and constants ```(e.g. x+y+6 = 5)```
>> When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
> ## Methods to solve a polynomial
>> 1. ```Combine like terms```
>> 2. ```Dividing polynomials```
>> 3. ```Multiplying polynomials```
> ## Simplifying Alegebraic Expressions
>> An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.
> ## Factoring
>>Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic
>> equation (ax2 + bx + c). As well, simplify the polynomial, so that all common factors are outside
>> (e.g 5x + 10 = 5(x + 2) ).
>> |Type of Polynomial|Definition|
>> |:-----------------|:---------|
>> |Monomial|Polynomial that only has one term|
>> |Binomial|Polynomial that only has 2 terms|
>> |Trinomial|polynomial that only has 3 terms|
>> |Type|Example|
>> |:--:|:-----:|
>> |Perfect Square Trinomials| (a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b|
>> |Difference with Squares|a2-b2 = (a+b)(a-b)|
>> |Simple Trinomials|x2+6x-7 = (x+7)(x-1)|
>> |Complex Trinomials|2x2-21x-11 = (2x+1)(x-11)|
>> |Common Factor|2ab+6b+4 = 2(ab+3b+2)|
>> |Factor By Grouping|ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)|
> ## Shortcuts
>>  > ## Foil / Rainbow Method
>>
> ## Foil / Rainbow Method
>>  > ## Definitions
>> ```Term``` a variable that may have coefficient(s) or a constant
>> ```Alebraic Expressions```: made up of one or more terms
>> ```Like-terms```: same variables raised to the same exponent
> ## Tips
>> Be sure to factor fully
>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
>> Remember your formulas
>> Simplify first, combine like terms
# Solving Equations and Inequailties (3)
> ## Equations
>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
>> To ```solve``` and equation is to find the variable that makes the statement true
>> ### Methods to solve an equation
>>> 1. Expand and simplify both sides
>>> 2. Isolate using reverse order of operations
>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
>
> ## Absolute Values
>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
>> equations will have the absolute bracket be positive while the other negative.
>> Absolute values are written in the form ```| x |```
>> where
>> if x > 0, | x | = x
>> if x = 0, | x | = 0
>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
>> Solve quadratic equation by:
>> 1. Isolation
>> a(x+b)2 + k = 0
>> 2. Factor using zero-product property
>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
>> (x-a)(x-b)=0
>> x = a, b
>>
> ## Definitions
>> ```Term``` a variable that may have coefficient(s) or a constant
>> ```Alebraic Expressions```: made up of one or more terms
>> ```Like-terms```: same variables raised to the same exponent
> ## Tips
>> Be sure to factor fully
>> Learn the ```criss-cross``` (not mandatory but its a really good method to factor quadratics)
>> Learn ```long division``` (not mandatory but its a really good method to find factors of an expression)
>> Remember your formulas
>> Simplify first, combine like terms
# Solving Equations and Inequailties (3)
> ## Equations
>> a ```mathematical statement``` in which the value on the ```left side``` equals the value on the ```right side``` of the equal sign
>> To ```solve``` and equation is to find the variable that makes the statement true
>> ### Methods to solve an equation
>>> 1. Expand and simplify both sides
>>> 2. Isolate using reverse order of operations
>>> 3. Check the solution by plugging the variable back into the equation and check if the ```left side``` equals the ```right side```
>
> ## Absolute Values
>> There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the
>> equations will have the absolute bracket be positive while the other negative.
>> Absolute values are written in the form ```| x |```
>> where
>> if x > 0, | x | = x
>> if x = 0, | x | = 0
>> if x < 0, | x | = -x
> ## Quadractic Equations
>> ```Quadratic Function```: A parabolic graph where the axis of symmetry is parallel to the y-axis
>> ```Quadratic Equation```: This function is set equal to ```0```. The solution to the equation are called ```roots```
>> Solve quadratic equation by:
>> 1. Isolation
>> a(x+b)2 + k = 0
>> 2. Factor using zero-product property
>> ```The Zero Factor Property``` refers to when a×b=0, then either a=0 or b=0.
>> (x-a)(x-b)=0
>> x = a, b
>>  >> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
> ## Tips
>> ```Absolute Values``` can have 2 solutions
>> ```Quadratics``` can also have 2 solutions
>> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
# Measurement and Geometry (4)
> ## Angle Theorems
> 1. ```Transversal Parallel Line Theorems``` (TPT)
> a. Alternate Angles are Equal ```(Z-Pattern)```
> b. Corresponding Angles Equal ```(F-Pattern)```
> c. Interior Angles add up to 180 ```(C-Pattern)```
>
>> Note:
>> √x2 = ± x (There are 2 possible solutions)
>> ```Distrubutive Property``` - This is opening the bracket. a(x+y) = ax+ay
> ## Tips
>> ```Absolute Values``` can have 2 solutions
>> ```Quadratics``` can also have 2 solutions
>> Make sure to do the reverse when moving things to the other side, meaning a positive on the ```left side``` becomes a negative on the ```right side```
# Measurement and Geometry (4)
> ## Angle Theorems
> 1. ```Transversal Parallel Line Theorems``` (TPT)
> a. Alternate Angles are Equal ```(Z-Pattern)```
> b. Corresponding Angles Equal ```(F-Pattern)```
> c. Interior Angles add up to 180 ```(C-Pattern)```
>  > 2. ```Supplementary Angle Triangle``` (SAT)
> - When two angles add up to 180 degrees
>
> 2. ```Supplementary Angle Triangle``` (SAT)
> - When two angles add up to 180 degrees
>  > 3. ```Opposite Angle Theorem (OAT)``` (OAT)
> - Two lines intersect, two angles form opposite. They have equal measures
>
> 3. ```Opposite Angle Theorem (OAT)``` (OAT)
> - Two lines intersect, two angles form opposite. They have equal measures
>  > 4. ```Complementary Angle Theorem``` (CAT)
> - The sum of two angles that add up to 90 degrees
>
> 4. ```Complementary Angle Theorem``` (CAT)
> - The sum of two angles that add up to 90 degrees
>  > 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
> - The sum of the three interior angles of any triangle is 180 degrees
>
> 5. ```Angle Sum of a Triangle Theorem``` (ASTT)
> - The sum of the three interior angles of any triangle is 180 degrees
>  > 6. ```Exterior Angle Theorem``` (EAT)
> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
>
> 6. ```Exterior Angle Theorem``` (EAT)
> - The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
>  > 7. ``` Isosceles Triangle Theorem``` (ITT)
> - The base angles in any isosceles triangle are equal
>
> 7. ``` Isosceles Triangle Theorem``` (ITT)
> - The base angles in any isosceles triangle are equal
>  > 8. ```Sum of The Interior Angle of a Polygon```
> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
> 8. ```Sum of The Interior Angle of a Polygon```
> - The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
 > 9. ```Exterior Angles of a Convex Polygon```
> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
> 9. ```Exterior Angles of a Convex Polygon```
> - The sum of the exterior angle of any convex polygon is always ```360 degrees```
 > ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
>> |Figure|Properties|
>> |:-----|:---------|
>> |Scalene Triangle|no sides equal|Length of line segment|
>> |Isosceles Triangle| two sides equal|Length of line segment|
>> |Equilateral Triangle|All sides equal|Length of line segment|
>> |Right Angle Triangle|Two sides are perpendicular to each other|
>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
>> |Kite|The diagonals are perpendicular|
> ## 2D Geometry Equations
>> |Shape|Formula|Picture|
>> |:----|:------|:------|
>> |Rectangle|```Area```: lw
> ## Properties of Quadrilaterals
>> Determine the shape using the properties of it
>> |Figure|Properties|
>> |:-----|:---------|
>> |Scalene Triangle|no sides equal|Length of line segment|
>> |Isosceles Triangle| two sides equal|Length of line segment|
>> |Equilateral Triangle|All sides equal|Length of line segment|
>> |Right Angle Triangle|Two sides are perpendicular to each other|
>> |Parallelogram|Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other|
>> |Rectangle|Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length|
>> |Square|All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals|
>> |Rhombus|Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular|
>> |Trapezoid|There is one pair of opposite sides and they are parallel and unequal in length|
>> |Kite|The diagonals are perpendicular|
> ## 2D Geometry Equations
>> |Shape|Formula|Picture|
>> |:----|:------|:------|
>> |Rectangle|```Area```: lw  > ## Median
>> Each median divides the triangle into 2 smaller triangles of equal area
>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
>>
> ## Median
>> Each median divides the triangle into 2 smaller triangles of equal area
>> The centroid is exactly 2⁄3 they way of each median from the vertex, or 1⁄3 the way from the midpoint of the opposite side, or ```2:1``` ratio
>> The three medians divide the triangle into ```6``` smaller triangles of equal area and ```3 pairs``` of congruent triangles
>>  > ## Terms:
>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
>>>
> ## Terms:
>> ```Altitude``` The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
>> ```Orthocenter```: where all 3 altitudes of the triangle intersect
>>>  >> ```Midpoint```: A point on a line where the length of either side of the point are equal
>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
>> ```Centroid```: The intersection of the 3 medians of a triangle
>>>
>> ```Midpoint```: A point on a line where the length of either side of the point are equal
>> ```Median```: A line segment joining the vertex to the midpoint of the opposite side
>> ```Midsegment```: A line joining 2 midpoints of the 2 sides of a triangle
>> ```Centroid```: The intersection of the 3 medians of a triangle
>>>  > ## Proportionality theorem:
>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
>>
> ## Proportionality theorem:
>> The midsegment of a triangle is ```half``` the length of the opposite side and ```parallel``` to the opposite side
>> Three midsegment of a triangle divide ```4 congruent``` triangles with the same area
>> The Ratio of the outer triangle to the triangle created by the 3 midsegments is ```4 to 1```
>>  > ## Definitions
>> ```Parallel```: 2 lines with the same slope
>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
>> ```Collinear Points```: points that line on the same straight line
> ## Variables
>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
> ## Statistics
>> ```Interpolation```: Data **inside** the given data set range.
>> ```Extrapolation```: Data **outside** the data set range.
>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
>> and it represents the trend of a graph.
>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
> ## Time - Distance Graph
>> Time is the independent variable and distance is the dependent variable
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
>>
> ## Definitions
>> ```Parallel```: 2 lines with the same slope
>> ```Perpendicular```: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
>> ```Domain```: The **ordered** set of all possible values of the independent variable (x).
>> ```Range```: The **ordered** set of all possible values of the dependent variable (y).
>> ```Continous Data```: A data set that can be broken into smaller parts. This is represented by a ```Solid line```.
>> ```Discrete Data```: A data set that **cannot** be broken into smaller parts. This is represented by a ```Dashed line```.
>> ```First Difference```: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
>> ```Collinear Points```: points that line on the same straight line
> ## Variables
>> ```Independent Variable```: A Variable in a relation which the values can be chosen or isn't affected by anything.
>> ```Dependent Varaible```: A Variable in a relation which is **dependent** on the independent variable.
> ## Statistics
>> ```Interpolation```: Data **inside** the given data set range.
>> ```Extrapolation```: Data **outside** the data set range.
>> ```Line of Best Fit```: A line that goes through as many points as possible, and the points are the closest on either side of the line,
>> and it represents the trend of a graph.
>> ```Coefficient of Correlation```: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
>> ```Partial Variation```: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.
> ## Time - Distance Graph
>> Time is the independent variable and distance is the dependent variable
>> You can't go backwards on the x-axis, as you can't go back in time
>> Plot the points accordingly
>> Draw the lines accordingly
>>  >> **Direction is always referring to:**
>> 1. ```go towards home```
>> 2. ```going away from home```
>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
>>
>> **Direction is always referring to:**
>> 1. ```go towards home```
>> 2. ```going away from home```
>> 3. ```stop```
> ## Scatterplot and Line of Best Fit
>> A scatterplot graph is there to show the relation between two variables in a table of values.
>> A line of best fit is a straight line that describes the relation between two variables.
>> If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.
>>  >> ### How To Determine the Equation Of a Line of Best Fit
>> 1. Find two points **```ON```** the ```line of best fit```
>> 2. Determine the ```slope``` using the two points
>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
>>| y | x |First Difference|
>>|:--|:--|:---------------|
>>|-1|-2|1|
>>|0|-1|1|
>>|1|0|1|
>>|2|1|1|
>>|3|2|1|
>>|4|3|1|
> ## Tips
>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
>> Draw your ```Line of Best Fit``` correctly
>> Read the word problems carefully, and make sure you understand it when graphing things
>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
>> Label your lines
# System of Equations (6)
> ## Linear System
>> Two or more equation that you are working on all together at once on the same set of axes.
>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
>> when **Profit = 0**. There is no gain or loss.
>> ### Number of Solutions
>>>
>> ### How To Determine the Equation Of a Line of Best Fit
>> 1. Find two points **```ON```** the ```line of best fit```
>> 2. Determine the ```slope``` using the two points
>> 3. Use ```point-slope form``` to find the equation of the ```line of best fit```
> ## Table of values
>> To find first differences or any points on the line, you can use a ```table of values```
>>| y | x |First Difference|
>>|:--|:--|:---------------|
>>|-1|-2|1|
>>|0|-1|1|
>>|1|0|1|
>>|2|1|1|
>>|3|2|1|
>>|4|3|1|
> ## Tips
>> Label your graph correctly, the scales/scaling and always the ```independent variable``` on the ```x-axis``` and the ```dependent variable``` on ```y-axis```
>> Draw your ```Line of Best Fit``` correctly
>> Read the word problems carefully, and make sure you understand it when graphing things
>> Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
>> Label your lines
# System of Equations (6)
> ## Linear System
>> Two or more equation that you are working on all together at once on the same set of axes.
>> The lines may ```cross``` or ```intersect``` at a point called the ```Point of Intersection (POI)```.
>> The coordinated of the ```POI``` must satisfy the equation of all the lines in a linear equation.
>> In business, the ```Point of Intersection``` is known as the **Break Even Point** where ```Revenue - Cost = Profit```
>> when **Profit = 0**. There is no gain or loss.
>> ### Number of Solutions
>>>  > ## Solving Linear-Quadratic Systems
>> To find the point of intersection, do the following:
>> 1. Isolate both equations for ```y```
>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
>> 3. Simplify and put everything on one side and equal to zero on the other side
>> 4. Factor
>> 5. Use zero-product property to solve for all possible x-values
>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
>> 7. State a conclusion / the solution
>>
> ## Solving Linear-Quadratic Systems
>> To find the point of intersection, do the following:
>> 1. Isolate both equations for ```y```
>> 2. Set the equations equal to each other by ```subsitution``` Equation 1 = Equation 2
>> 3. Simplify and put everything on one side and equal to zero on the other side
>> 4. Factor
>> 5. Use zero-product property to solve for all possible x-values
>> 6. Subsitute the x-values to one of the original equations to solve for all y-values
>> 7. State a conclusion / the solution
>>  > ## Tips
>> Read the questions carefully and model the system of equations correctly
>> Be sure to name your equations
>> Label your lines
# General Tips
> Be sure to watch out for units, like ```cm``` or ```km```
> Watch out for ```+/-```
> Be sure to reverse the operation when moving things to the other side of the equation
> Make sure to have a proper scale for graphs
> Read question carefully and use the appropriate tools to solve
> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
> ## Word Problems
>> Read carefully
>> model equations correctly
>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
> ## Graph Problems
>> Look up on tips in units (5) and (6)
>> be sure to use a ruler when graphing
> ## System of Equations
>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
> Ryan Mark - He helped provide alot of information for me
> Magicalsoup - ME!
> ## Tips
>> Read the questions carefully and model the system of equations correctly
>> Be sure to name your equations
>> Label your lines
# General Tips
> Be sure to watch out for units, like ```cm``` or ```km```
> Watch out for ```+/-```
> Be sure to reverse the operation when moving things to the other side of the equation
> Make sure to have a proper scale for graphs
> Read question carefully and use the appropriate tools to solve
> **WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!**
> ## Word Problems
>> Read carefully
>> model equations correctly
>> ```Reread``` the question over and over again until you fully understand it and made sure there is no tricks. :p
> ## Graph Problems
>> Look up on tips in units (5) and (6)
>> be sure to use a ruler when graphing
> ## System of Equations
>> When in doubt or to check your work, just plug the numbers back in and check if the statement is true
# Credits
> Ryan Mark - He helped provide alot of information for me
> Magicalsoup - ME!