## Angle Theorems
1. ```Transversal Parallel Line Theorems``` (TPT)
a. Alternate Angles are Equal ```(Z-Pattern)```
b. Corresponding Angles Equal ```(F-Pattern)```
c. Interior Angles add up to 180 ```(C-Pattern)```
- 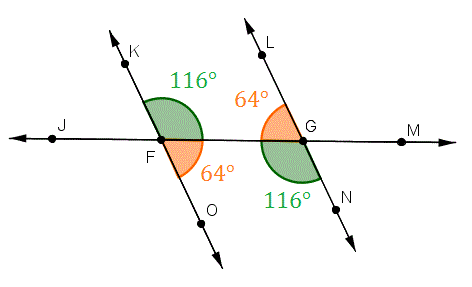 2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-
2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-  3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-
3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
- 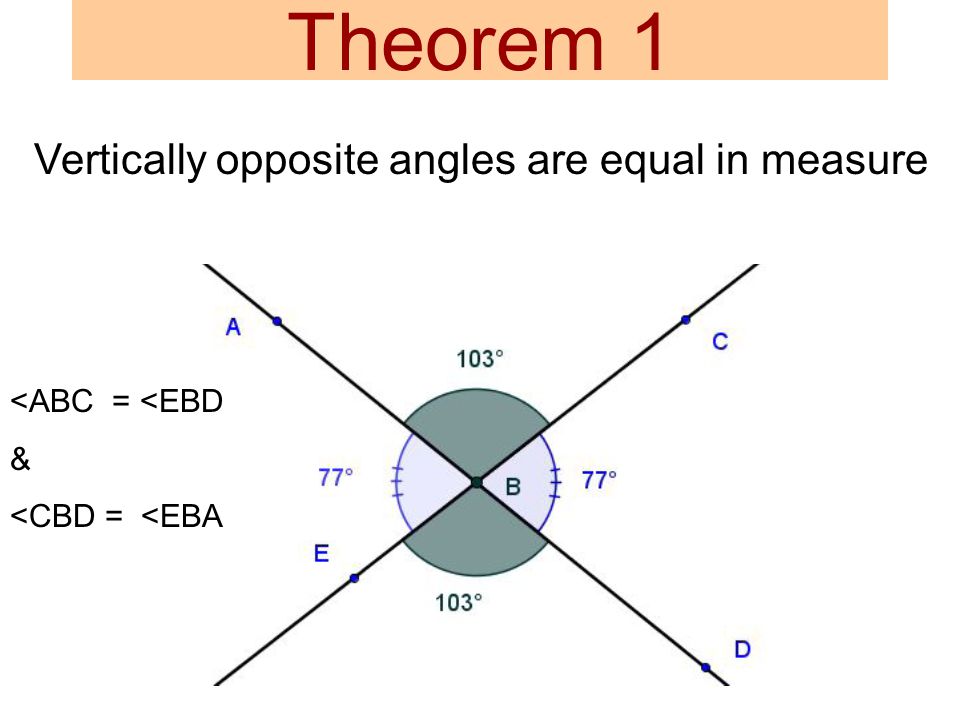 4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-
4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-  5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-
5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-  6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
- 7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-
7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-  8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-
8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-  9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-
9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-  ## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal.
## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal.
 2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-
2. ```Supplementary Angle Triangle``` (SAT)
- When two angles add up to 180 degrees
-  3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-
3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-  4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-
4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-  5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-
5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-  6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
- 7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-
7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-  8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-
8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-  9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-
9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-  ## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal.
## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
## Similary Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
### Side Angle Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal.