# Unit 4: Trigonometry
## Angle Theorems
1. ```Transversal Parallel Line Theorems``` (TPT)
a. Alternate Angles are Equal ```(Z-Pattern)```
b. Corresponding Angles Equal ```(F-Pattern)```
c. Interior Angles add up to 180 ```(C-Pattern)```
-  2. ```Supplementary Angle Theorem``` (SAT)
- When two angles add up to 180 degrees
-
2. ```Supplementary Angle Theorem``` (SAT)
- When two angles add up to 180 degrees
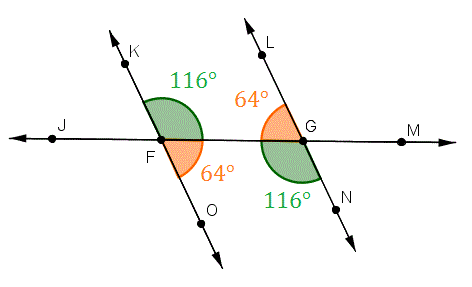
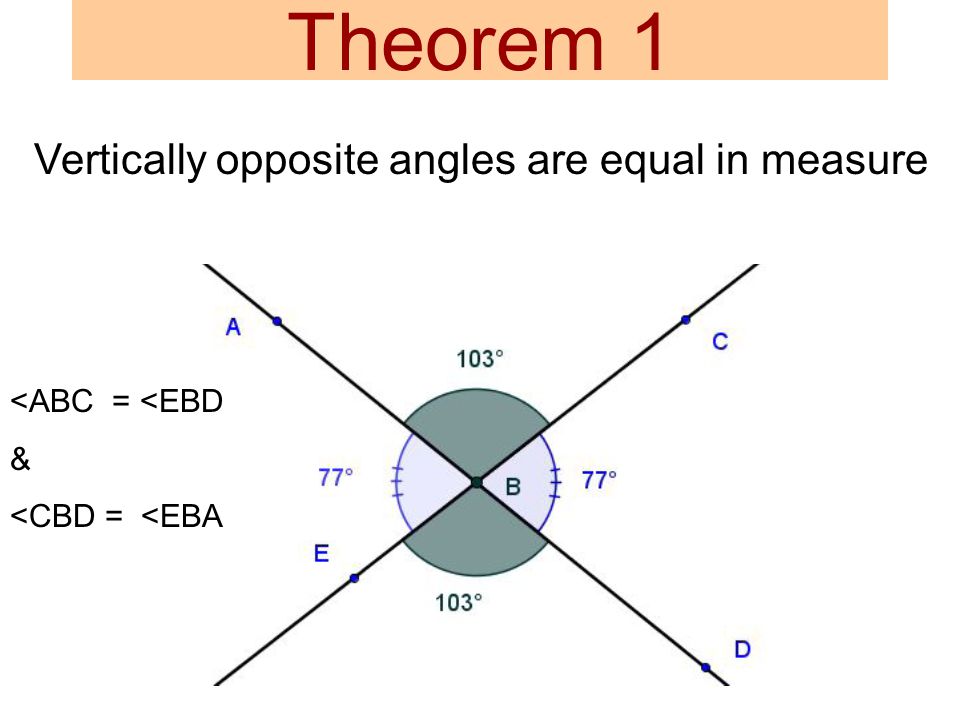
-  3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-
3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-  4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-
4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-  5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-
5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-  6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
- 7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-
7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-  8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-
8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-  9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-
9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-  ## Congruency
`Congruent`: Same size and shape
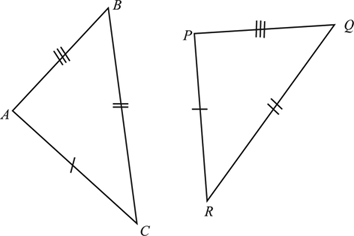
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
 ### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
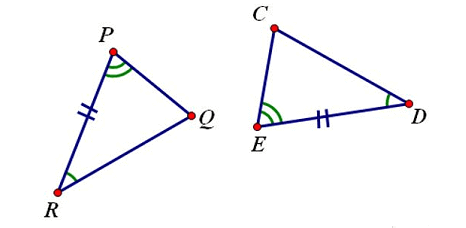
 ### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
 ## Similar Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
## Similar Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
 ### Side-Angle-Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
### Side-Angle-Side similarity (RAR $`\sim`$)
Two pairs of corresponding sides are proportional and the **contained** angle are equal.
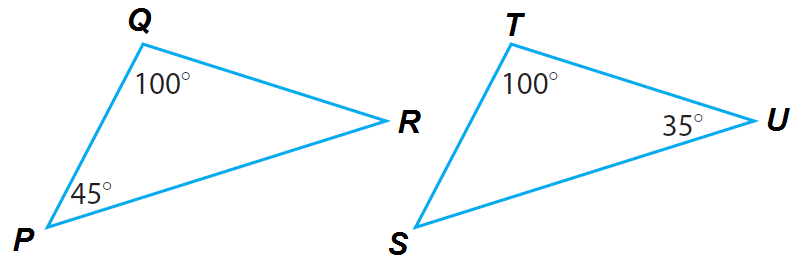
 ### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
 ## Primary Trigonometric Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary trigonometric ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram|
## Primary Trigonometric Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary trigonometric ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram| |
| |
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
|
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
 ## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle-side-side. The sine law calculation may need to give 0, 1, or 2 solutions.
In the ambiguous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 |
## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle-side-side. The sine law calculation may need to give 0, 1, or 2 solutions.
In the ambiguous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 | |$`a \lt h`$|no triangle exists|
|2 |
|$`a \lt h`$|no triangle exists|
|2 | |$`a = h`$|one triangle exists|
|3 |
|$`a = h`$|one triangle exists|
|3 |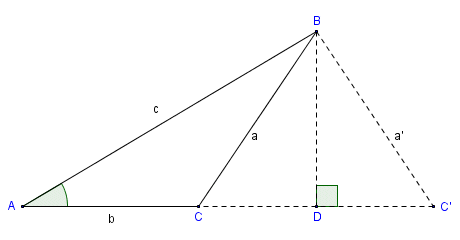 |$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 |
|$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 | |$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 |
|$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 | |$`a \le b`$|no triangles exist|
|6 |
|$`a \le b`$|no triangles exist|
|6 | |$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearings`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees directly to the second letter (N, E, S, W)
**Note:** Northeast, southeast, northwest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats, etc.) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometric ratios whenever necessary.
|$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearings`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees directly to the second letter (N, E, S, W)
**Note:** Northeast, southeast, northwest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats, etc.) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometric ratios whenever necessary.
 2. ```Supplementary Angle Theorem``` (SAT)
- When two angles add up to 180 degrees
-
2. ```Supplementary Angle Theorem``` (SAT)
- When two angles add up to 180 degrees
-  3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-
3. ```Opposite Angle Theorem (OAT)``` (OAT)
- Two lines intersect, two angles form opposite. They have equal measures
-  4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-
4. ```Complementary Angle Theorem``` (CAT)
- The sum of two angles that add up to 90 degrees
-  5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-
5. ```Angle Sum of a Triangle Theorem``` (ASTT)
- The sum of the three interior angles of any triangle is 180 degrees
-  6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
6. ```Exterior Angle Theorem``` (EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
- 7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-
7. ``` Isosceles Triangle Theorem``` (ITT)
- The base angles in any isosceles triangle are equal
-  8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-
8. ```Sum of The Interior Angle of a Polygon```
- The sum of the interioir angles of any polygon is ```180(n-2)``` or ```180n - 360```, where ```n``` is the number of sides of the polygon
-  9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-
9. ```Exterior Angles of a Convex Polygon```
- The sum of the exterior angle of any convex polygon is always ```360 degrees```
-  ## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
## Congruency
`Congruent`: Same size and shape
### Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
 ### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
### Side-Angle-Side (SAS)
If two sides and the **contained** angle of a triangle are respectively equal to two sides and the **contained** angle of another triangle, then the triangles are congruent.
 ### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
### Angle-Side-Angle (ASA)
If two angles and the **contained** side of a triangle are respectively equal to two angles and the **contained** side of another triangle, then the triangles are congruent.
 ## Similar Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
## Similar Triangles
`Similar`: Same shape but different sizes (one is an enlargement of the other)
### Properties
Lets say we have $`\triangle ABC \sim \triangle DEF`$
1. Corresponding angles are **equal**
- $`\angle A = \angle D`$
- $`\angle B = \angle E`$
- $`\angle C = \angle F`$
2. Corresponding side are **proportional**.
- $`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`$
3. Proportional Area
- Let $`k`$ be the **scale factor**, when concerning for triangle area, if the triangle area can be defined as $`\dfrac{bh}{2}`$, then by using the smaller triangles side lengths
our big triangle's area is equal to $`\dfrac{k^2bh}{2}`$. Similar equations and agruments can be dervied from this
### Side-Side-Side similarity (RRR $`\sim`$)
Three pairs of corresponding sides are in the **same ratio**
 ### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
### Angle-Angle similarity (AA $`\sim`$)
Two pairs of corresponding angles are equal. In the diagram below, we can solve for the missing angle using Angle Sum Of A Triangle Theorem (ASTT) and see that those 2 triangle's angles are equal.
 ## Primary Trigonometric Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary trigonometric ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram|
## Primary Trigonometric Ratios
|Part Of Triangle|Property|
|:---------------|:-------|
|Hypotenuse|The longest side of the right triangle. it is across the $`90^o`$ (right angle)|
|Opposite|The side opposite to the reference angle|
|Adjacent|The side next to the reference agnle|
**Remember**: Primary trigonometric ratios are only used to find the **acute** angles or sides of a **right-angled** triangle
### SOH CAH TOA
**SINE** $`\sin \theta = \dfrac{\text{Opposite}}{\text{Hypotenuse}}`$
**COSINE** $`\cos \theta = \dfrac{\text{Adajacent}}{\text{Hypotenuse}}`$
**TANGENT** $`\tan \theta = \dfrac{\text{Opposite}}{\text{Adajacent}}`$
## Angle Of Elevation And Depression
| |Angle of Elevation|Angle of Depression|
|:---------|:-----------------|:------------------|
|Definition|**Angle of Elevation** is the angle from the horizontal looking **up** to some object|**Angle of Depression** is the angle frorm the horizontal looking **down** to some object|
|Diagram| |
| |
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
|
We can see that **Angle of Elevation = Angle of Depression** in the diagram below (Proven using Z-pattern)
 ## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle-side-side. The sine law calculation may need to give 0, 1, or 2 solutions.
In the ambiguous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 |
## Sine Law
In any $`\triangle ABC`$: $`\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}`$ or $`\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}`$
We can derive the formula further to get:
- $`\dfrac{\sin A}{\sin B} = \dfrac{a}{b}`$
- $`\dfrac{\sin A}{\sin C} = \dfrac{a}{c}`$
- $`\dfrac{\sin B}{\sin C} = \dfrac{b}{c}`$
Also, for some trigonometry identities:
- $`\tan x = \dfrac{\sin x}{\cos x}`$
- $`\sin^2 A + \cos^2 A = 1`$
**If you are finding the sides or agnles of an `oblique triangle` given 1 side, its opposite angle and one other side or angle, use the sine law.**
### Ambiguous Case
The ambiguous case arises in the SSA or (ASS) case of an triangle, when you are given angle-side-side. The sine law calculation may need to give 0, 1, or 2 solutions.
In the ambiguous case, if $`\angle A, a, b`$ are given, the height of the triangle is $`h= b\sin A`$
|Case|If $`\angle A`$ is **acute**|Condition|# & Type of triangles possible|
|:---|:---------------------------|:--------|:-----------------------------|
|1 | |$`a = h`$|one triangle exists|
|3 |
|$`a = h`$|one triangle exists|
|3 | |$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 |
|$`h \lt a \lt b`$|two triangle exist (one acute triangle, one obtuse triangle)|
|4 | |$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 |
|$`a \ge b`$|one triangle exists|
|Case|If $`\angle A`$ is **obtuse**|Condition|# & Type of triangles possible|
|:---|:----------------------------|:--------|:-----------------------------|
|5 | |$`a \le b`$|no triangles exist|
|6 |
|$`a \le b`$|no triangles exist|
|6 | |$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearings`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees directly to the second letter (N, E, S, W)
**Note:** Northeast, southeast, northwest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats, etc.) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometric ratios whenever necessary.
|$`a \gt b`$|one triangle exists|
## Cosine Law
In any $`\triangle ABC`$, $`c^2 = a^2 + b^2 - 2ab\cose C`$
**If you are given 3 sides or 2 sides and the contained angle of an `oblique triangle`, then use the consine law**
## Directions
`Bearings`: **Always** start from **North**, and goes **clockwise**
`Direction`: Start from the first letter (N, E, S, W), and go that many degrees directly to the second letter (N, E, S, W)
**Note:** Northeast, southeast, northwest etc. all have 45 degrees to the left or the right from their starting degree (0, 90, 180, 270)
## 2D Problems
**Note:** Watch out for the case where you don't know which side the 2 things (buildings, boats, etc.) are, they can result in 2 answers
## 3D problems
**Note:** Use angle theorems to find bearing/direction angle, and to help with the problem in general. Apply sine law, cosine law, and primary trigonometric ratios whenever necessary.