# MATH 117: Calculus 1
## Functions
A **function** is a rule where each input has exactly one output, which can be determined by the **vertical line test**.
!!! definition
- The **domain** is the set of allowable independent values.
- The **range** is the set of allowable dependent values.
Functions can be **composed** to apply the result of one function to another.
$$
(f\circ g)(x) = f(g(x))
$$
!!! warning
Composition is not commutative: $f\circ g \neq g\circ f$.
## Inverse functions
The inverse of a function swaps the domain and range of the original function: $f^{-1}(x)$ is the inverse of $f(x)$.. It can be determined by solving for the other variable:
$$
\begin{align*}
y&=mx+b \\
y-b&=mx \\
x&=\frac{y-b}{m}
\end{align*}
$$
Because the domain and range are simply swapped, the inverse function is just the original function reflected across the line $y=x$.
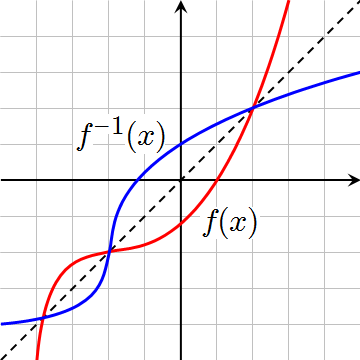 (Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example
(Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example
 (Source: Wikimedia Commons, public domain)
By restricting the domain to $[0,\inf]$, the **multivalued inverse function** $y=\pm\sqrt{x}$ is reduced to just the partial inverse $y=\sqrt{x}$.
## Symmetry
78u7u887878
An **even function** satisfies the property that $f(x)=f(-x)$, indicating that it is unchanged by a reflection across the y-axis.
An **odd function** satisfies the property that $-f(x)=f(-x)$, indicating that it is unchanged by a 180° rotation about the origin.
The following properties are always true for even and odd functions:
- even × even = even
- odd × odd = even
- even × odd = odd
Functions that are symmetric (that is, both $f(x)$ and $f(-x)$ exist) can be split into an even and odd component. Where $g(x)$ is the even component and $h(x)$ is the odd component:
$$
\begin{align*}
f(x) &= g(x) + h(x) \\
g(x) &= \frac{1}{2}(f(x) + f(-x)) \\
h(x) &= \frac{1}{2}(f(x) - f(-x))
\end{align*}
$$
!!! note
The hyperbolic sine and cosine are the even and odd components of $f(x)=e^x$.
$$
\cosh x = \frac{1}{2}(e^x + e^{-x}) \\
\sinh x = \frac{1}{2}(e^x - e^{-x})
$$
## Piecewise functions
A piecewise function is one that changes formulae at certain intervals. To solve piecewise functions, each of one's intervals should be considered.
### Absolute value function
$$
\begin{align*}
|x| = \begin{cases}
x &\text{ if } x\geq 0 \\
-x &\text{ if } x < 0
\end{cases}
\end{align*}
$$
### Signum function
The signum function returns the sign of its argument.
$$
\begin{align*}
\text{sgn}(x)=\begin{cases}
-1 &\text{ if } x < 0 \\
0 &\text{ if } x = 0 \\
1 &\text{ if } x > 0
\end{cases}
\end{align*}
$$
### Ramp function
The ramp function makes a ramp through the origin that suddenly flatlines at 0. Where $c$ is a constant:
$$
\begin{align*}
r(t)=\begin{cases}
0 &\text{ if } x \leq 0 \\
ct &\text{ if } x > 0
\end{cases}
\end{align*}
$$
(Source: Wikimedia Commons, public domain)
By restricting the domain to $[0,\inf]$, the **multivalued inverse function** $y=\pm\sqrt{x}$ is reduced to just the partial inverse $y=\sqrt{x}$.
## Symmetry
78u7u887878
An **even function** satisfies the property that $f(x)=f(-x)$, indicating that it is unchanged by a reflection across the y-axis.
An **odd function** satisfies the property that $-f(x)=f(-x)$, indicating that it is unchanged by a 180° rotation about the origin.
The following properties are always true for even and odd functions:
- even × even = even
- odd × odd = even
- even × odd = odd
Functions that are symmetric (that is, both $f(x)$ and $f(-x)$ exist) can be split into an even and odd component. Where $g(x)$ is the even component and $h(x)$ is the odd component:
$$
\begin{align*}
f(x) &= g(x) + h(x) \\
g(x) &= \frac{1}{2}(f(x) + f(-x)) \\
h(x) &= \frac{1}{2}(f(x) - f(-x))
\end{align*}
$$
!!! note
The hyperbolic sine and cosine are the even and odd components of $f(x)=e^x$.
$$
\cosh x = \frac{1}{2}(e^x + e^{-x}) \\
\sinh x = \frac{1}{2}(e^x - e^{-x})
$$
## Piecewise functions
A piecewise function is one that changes formulae at certain intervals. To solve piecewise functions, each of one's intervals should be considered.
### Absolute value function
$$
\begin{align*}
|x| = \begin{cases}
x &\text{ if } x\geq 0 \\
-x &\text{ if } x < 0
\end{cases}
\end{align*}
$$
### Signum function
The signum function returns the sign of its argument.
$$
\begin{align*}
\text{sgn}(x)=\begin{cases}
-1 &\text{ if } x < 0 \\
0 &\text{ if } x = 0 \\
1 &\text{ if } x > 0
\end{cases}
\end{align*}
$$
### Ramp function
The ramp function makes a ramp through the origin that suddenly flatlines at 0. Where $c$ is a constant:
$$
\begin{align*}
r(t)=\begin{cases}
0 &\text{ if } x \leq 0 \\
ct &\text{ if } x > 0
\end{cases}
\end{align*}
$$
 (Source: Wikimedia Commons, public domain)
### Floor and ceiling functions
The floor function rounds down.
$$\lfloor x\rfloor$$
The ceiling function rounds up.
$$\lceil x \rceil$$
### Fractional part function
In a nutshell, the fractional part function:
- returns the part **after the decimal point** if the number is positive
- returns 1 - **the part after the decimal point** if the number is negative
$$\text{FRACPT}(x) = x-\lfloor x\rfloor$$
Because this function is periodic, it can be used to limit angles to the $[0, 2\pi)$ range with:
$$f(\theta) = 2\pi\cdot\text{FRACPT}\biggr(\frac{\theta}{2\pi}\biggr)$$
### Heaviside function
The Heaviside function effectively returns a boolean whether the number is greater than 0.
$$
\begin{align*}
H(x) = \begin{cases}
0 &\text{ if } t < 0 \\
1 &\text{ if } t \geq 0
\end{cases}
\end{align*}
$$
This can be used to construct other piecewise functions by enabling them with $H(x-a)$ as a factor, where $a$ is the interval.
In a nutshell:
- $1-H(t-a)$ lets you "turn a function off" at at $t=a$
- $H(t-a)$ lets you "turn a function on at $t=a$
- $H(t-a) - H(t-b)$ leaves a function on in the interval $(a, b)$
!!! example
TODO: example for converting piecewise to heaviside via collecting heavisides
and vice versa
## Periodicity
The function $f(t)$ is periodic only if there is a repeating pattern, i.e. such that for every $x$, there is an $f(x) = f(x + nT)$, where $T$ is the period and $n$ is any integer.
### Circular motion
Please see [SL Physics 1#6.1 - Circular motion](/g11/sph3u7/#61-circular-motion) and its subcategory "Angular thingies" for more information.
## Partial function decomposition (PFD)
In order to PFD:
1. Factor the denominator into irreducibly quadratic or linear terms.
2. For each factor, create a term. Where capital letters below are constants:
- A linear factor $Bx+C$ has a term $\frac{A}{Bx+C}$.
- A quadratic factor $Dx^2+Ex+G$ has a term $\frac{H}{Dx^2+Ex+G}$.
3. Set the two equal to each other such that the denominators can be factored out.
4. Create systems of equations to solve for each constant.
!!! example
To decompose $\frac{x}{(x+1)(x^2+x+1)}$:
$$
\begin{align*}
\frac{x}{(x+1)(x^2+x+1)} &= \frac{A}{x+1} + \frac{Bx+C}{x^2+x+1} \\
&= \frac{A(x^2+x+1) + (Bx+C)(x+1)}{(x+1)(x^2+x+1)} \\
x &= A(x^2+x+1) + (Bx+C)(x+1) \\
0x^2 + x + 0 &= (Ax^2 + Bx^2) + (Ax + Bx + Cx) + (A + C) \\
\\
&\begin{cases}
0 = A + B \\
1 = A + B + C \\
0 = A + C
\end{cases}
\\
A &= -1 \\
B &= 1 \\
C &= 1 \\
\\
∴ \frac{x}{(x+1)(x^2+x+1)} &= -\frac{1}{x+1} + \frac{x + 1}{x^2 + x + 1}
\end{align*}
$$
(Source: Wikimedia Commons, public domain)
### Floor and ceiling functions
The floor function rounds down.
$$\lfloor x\rfloor$$
The ceiling function rounds up.
$$\lceil x \rceil$$
### Fractional part function
In a nutshell, the fractional part function:
- returns the part **after the decimal point** if the number is positive
- returns 1 - **the part after the decimal point** if the number is negative
$$\text{FRACPT}(x) = x-\lfloor x\rfloor$$
Because this function is periodic, it can be used to limit angles to the $[0, 2\pi)$ range with:
$$f(\theta) = 2\pi\cdot\text{FRACPT}\biggr(\frac{\theta}{2\pi}\biggr)$$
### Heaviside function
The Heaviside function effectively returns a boolean whether the number is greater than 0.
$$
\begin{align*}
H(x) = \begin{cases}
0 &\text{ if } t < 0 \\
1 &\text{ if } t \geq 0
\end{cases}
\end{align*}
$$
This can be used to construct other piecewise functions by enabling them with $H(x-a)$ as a factor, where $a$ is the interval.
In a nutshell:
- $1-H(t-a)$ lets you "turn a function off" at at $t=a$
- $H(t-a)$ lets you "turn a function on at $t=a$
- $H(t-a) - H(t-b)$ leaves a function on in the interval $(a, b)$
!!! example
TODO: example for converting piecewise to heaviside via collecting heavisides
and vice versa
## Periodicity
The function $f(t)$ is periodic only if there is a repeating pattern, i.e. such that for every $x$, there is an $f(x) = f(x + nT)$, where $T$ is the period and $n$ is any integer.
### Circular motion
Please see [SL Physics 1#6.1 - Circular motion](/g11/sph3u7/#61-circular-motion) and its subcategory "Angular thingies" for more information.
## Partial function decomposition (PFD)
In order to PFD:
1. Factor the denominator into irreducibly quadratic or linear terms.
2. For each factor, create a term. Where capital letters below are constants:
- A linear factor $Bx+C$ has a term $\frac{A}{Bx+C}$.
- A quadratic factor $Dx^2+Ex+G$ has a term $\frac{H}{Dx^2+Ex+G}$.
3. Set the two equal to each other such that the denominators can be factored out.
4. Create systems of equations to solve for each constant.
!!! example
To decompose $\frac{x}{(x+1)(x^2+x+1)}$:
$$
\begin{align*}
\frac{x}{(x+1)(x^2+x+1)} &= \frac{A}{x+1} + \frac{Bx+C}{x^2+x+1} \\
&= \frac{A(x^2+x+1) + (Bx+C)(x+1)}{(x+1)(x^2+x+1)} \\
x &= A(x^2+x+1) + (Bx+C)(x+1) \\
0x^2 + x + 0 &= (Ax^2 + Bx^2) + (Ax + Bx + Cx) + (A + C) \\
\\
&\begin{cases}
0 = A + B \\
1 = A + B + C \\
0 = A + C
\end{cases}
\\
A &= -1 \\
B &= 1 \\
C &= 1 \\
\\
∴ \frac{x}{(x+1)(x^2+x+1)} &= -\frac{1}{x+1} + \frac{x + 1}{x^2 + x + 1}
\end{align*}
$$
 (Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example
(Source: Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned.
$$f^{-1}(f(x)) = x$$
A function is **invertible** only if it is "**one-to-one**": each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a **partial inverse** to be defined.
!!! example