7.9 KiB
ECE 124: Digital Circuits
Base / radix conversion
Please see ECE 150: C++#Non-decimal numbers for more information.
Binary logic
A binary logic variable is a variable that has exactly two states:
- 0, or false (switch open)
- 1, or true (switch closed)
Binary logic functions are any function that satisfies the following type signature:
BoolFunc = Callable[[bool | BoolFunc, ...], bool]In other words:
- it must accept a number of booleans and/or other logic functions, and
- it must return exactly one boolean.
These can be expressed via truth table inputs/outputs, algebraically, or via a logical circuit schematic.
Logical operators
Operator precedence is () > NOT > AND > OR.
The AND operator returns true if and only if all arguments are true.
\[A\cdot B \text{ or }AB\]
(Source:
Wikimedia Commons)
The OR operator returns true if and only if at least one argument is true.
\[A+B\]
(Source:
Wikimedia Commons)
The NOT operator returns the opposite of its singular input.
\[\overline A \text{ or } A'\]
(Source:
Wikimedia Commons)
The NAND operator is equivalent to NOT AND.
\[\overline{A\cdot B}\]
(Source:
Wikimedia Commons)
The NOR operator is equivalent to NOT OR.
\[\overline{A+B}\]
(Source:
Wikimedia Commons)
NAND/NOR completeness
NAND and NOR are universal gates — some combination of them can form any other logic gate. Constructions of other gates using only these gates are called NAND-NAND realisations or NOR-NOR realisations.
This is useful in SOP as if two ANDs feed into an OR, all can be turned into NANDs to achieve the same result.
!!! example NOT can be expressed purely with NAND as \(A\) NAND \(A\):
<img src="https://upload.wikimedia.org/wikipedia/commons/3/3f/NOT_from_NAND.svg" width=150>(Source: Wikimedia Commons)</img>Postulates
In binary algebra, if \(x,y,z\in\mathbb B\) such that \(\mathbb B=\{0, 1\}\):
The identity element for AND \(1\) is such that any \(x\cdot 1 = x\).
The identity element for OR \(0\) is such that any \(x + 0 = x\).
In this space, it can be deduced that \(x+x'=1\) and \(x\cdot x'=0\).
De Morgan’s laws are much easier to express in boolean algebra, and denote distributing a negation by flipping the operator:
\[ (x\cdot y)'=x'+y' \\ (x+y)=x'\cdot y' \]
Please see ECE 108: Discrete Math 1#Operator laws for more information.
AND and OR are commutative.
- \(x\cdot y=y\cdot x\)
- \(x+y=y+x\)
AND and OR are associative.
- \(x\cdot(y\cdot z)=(x\cdot y)\cdot z)\)
- …
AND and OR are distributive with each other.
- \(x\cdot (y+z)=x\cdot y+z\cdot z\)
A term that depends on another term ORed together can be “absorbed”.
- \(x+x\cdot y=x\)
- \(x\cdot(x+y)=x\)
If a term being true also results in other ORed terms being true, it is redundant and can be eliminated via consensus.
- \(x\cdot y+y\cdot z+x'\cdot z=x\cdot
y+x'\cdot z\)
- if y and z are true, at least one of the other two terms must be true
- \((x+y)\cdot (y+z)\cdot(x'+z)=(x+y)\cdot (x'+z)\)
The synthesis of an algebraic formula represents its implementation via logic gates. In this course, its total cost is the sum of all inputs to all gates and the number of gates, excluding initial inputs of “true” or an initial negation.
In order to deduce an algebraic expression from a truth table, OR all of the rows in which the function returns true and simplify.
??? example Prove that \((x+y)\cdot(x+y')=x\):
\begin{align*}
\tag{distributive property}(x+y)\cdot(x+y')&=xx+xy'+yx+yy' \\
\tag{$yy'$ = 0, $xx=x$}&=x + xy' + yx \\
\tag{distributive, commutative properties}&= x(1+y'+y) \\
\tag{1 + ... = 1}&= x(1) \\
&=x
\end{align*}
Prove that $xy+yz+x'z=xy+x'z$:
\begin{align*}
\tag{$x+x'=1$}xy+yz+x'z&=xy+yz(x+x')+x'z \\
\tag{distributive property}&=xy+xyz+x'yz+x'z \\
\tag{distributive property}&=x(y+yz) + x'(yz+z) \\
\tag{distributive property}&=xy(1+z) + x'z(y+1) \\
\tag{$1+k=1$}&=xy(1) + x'z(1) \\
\tag{$1\cdot k=k$}&= xy+x'z
\end{align*}Minterms and maxterms
The minterm \(m\) is a product term where all variables in the function appear once. There are \(2^n\) minterms for each function, where \(n\) is the number of input variables.
To determine the relevant function, the subscript can be converted to binary and each function variable set such that:
- if the digit is \(1\), the complement is used, and
- if the digit is \(0\), the original is used.
\[m_j=x_1+x_2+\dots x_n\]
!!! example For a function that accepts three variables:
- there are eight minterms, from $m_0$ to $m_7$.
- the sixth minterm $m_6=xyz'$ because $6=0b110$.
For a sample function defined by the following minterms:
$$
\begin{align*}
f(x_1,x_2,x_3)&=\sum m(1,2,5) \\
&=m_1+m_2+m_5 \\
&=x_1x_2x_3' + x_1x_2'x_3 + x_1'x_2x_3'
\end{align*}
$$The maxterm \(M\) is a sum term where all variables in the function appear once. It is more or less the same as a minterm, except the condition for each variable is reversed (i.e., \(0\) indicates the complement).
\[M_j=x_1+x_2+\dots +x_n\]
!!! example For a sample function defined by the following maxterms:
\begin{align*}
f(x_1,x_2,x_3,x_4)&=\prod M(1,2,8,12) \\
&=M_1M_2M_8M_{12} \\
\end{align*}??? example Prove that \(\sum m(1,2,3,4,5,6,7)=x_1+x_2+x_3\): (some shortcuts taken for visual clarity)
\begin{align*}
\sum m(1,2,3,4,5,6,7) &=001+011+111+010+110+100+000 \\
\tag{SIMD distribution}&=001+010+100 \\
&=x_1+x_2+x_3
\end{align*}A canonical sum of products (SOP) is a function expressed as a sum of minterms.
\[f(x_1,x_2,\dots)=\sum m(a,b, \dots)\]
A canonical product of sums (POS) is a function expressed as a product of maxterms.
\[f(x_1,x_2,\dots)=\prod M(a,b,\dots)\]
Transistors
Binary is represented in hardware via switches called transistors. Above a certain voltage threshold, its output is \(1\), whlie it is \(0\) if below a threshold instead.
A transistor has three inputs/outputs:
- A ground
- An input source, which has voltage that determines whether the circuit is connected to the ground
- An output drain, which will either be grounded or have a voltage depending on whether the switch is closed.
(Source:
Wikimedia Commons)
A negative logic transistor uses a NOT bubble to represent that it is closed while the voltage is below a threshold.
(Source: Wikimedia Commons)
VHDL
VHDL is a hardware schematic language.
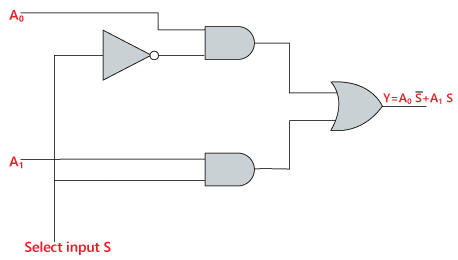
For example, the basic 2-to-1 multiplexer expressed above can be programmed as:
entity two_one_mux is
port (a0, s, a1 : in bit;
f : out bit);
end two_one_mux
architecture LogicFunc of two_one_mux is
begin
y <= (a0 AND s) OR (NOT s AND a1);
end LogicFunc;In this case, the inputs are a0, s, a1 that lead to an
output y. All input/output is of type bit (a
boolean).
The architecture defines how inputs translate to outputs via functions. These all run concurrently.