10 KiB
Unit 4: Measurement and Geometry
Angle Theorems
Transversal Parallel Line Theorems(TPT)- Alternate Angles are Equal
(Z-Pattern)
- Corresponding Angles Equal
(F-Pattern)
- Interior Angles add up to 180
(C-Pattern)
- Alternate Angles are Equal
Supplementary Angle Triangle(SAT)
When two angles add up to 180 degrees

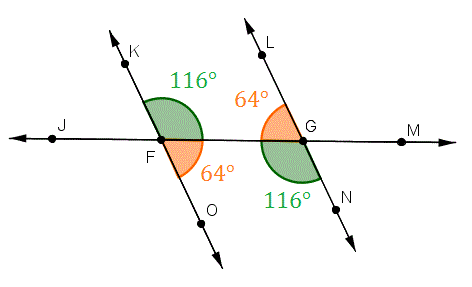
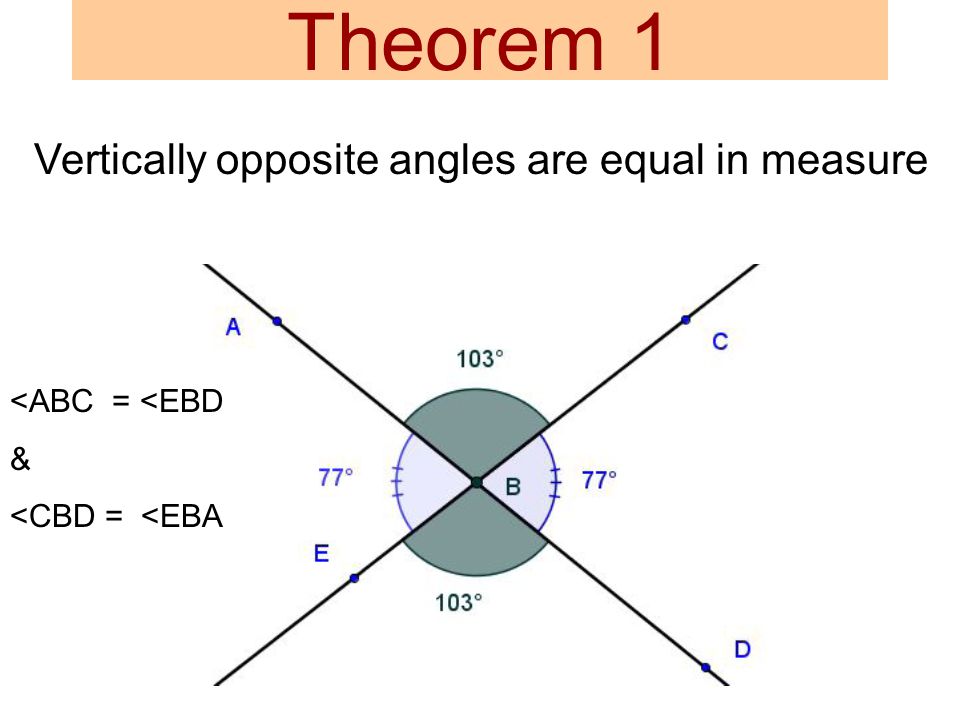
Opposite Angle Theorem (OAT)(OAT)
Two lines intersect, two angles form opposite. They have equal measures
Complementary Angle Theorem(CAT)
The sum of two angles that add up to 90 degrees

Angle Sum of a Triangle Theorem(ASTT)
The sum of the three interior angles of any triangle is 180 degrees

Exterior Angle Theorem(EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
Isosceles Triangle Theorem(ITT)
The base angles in any isosceles triangle are equal

Sum of The Interior Angle of a Polygon
The sum of the interioir angles of any polygon is
180(n-2)or180n - 360, wherenis the number of sides of the polygon
Exterior Angles of a Convex Polygon
The sum of the exterior angle of any convex polygon is always
360 degrees
Properties of Quadrilaterals
- Determine the shape using the properties of it
| Figure | Properties |
|---|---|
| Scalene Triangle | no sides equal |
| Isosceles Triangle | two sides equal |
| Equilateral Triangle | All sides equal |
| Right Angle Triangle | Two sides are perpendicular to each other |
| Parallelogram | Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other |
| Rectangle | Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length |
| Square | All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals |
| Rhombus | Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular |
| Trapezoid | There is one pair of opposite sides and they are parallel and unequal in length |
| Kite | The diagonals are perpendicular |
2D Geometry Equations
| Shape | Formula | Picture |
|---|---|---|
| Rectangle | Area: \(`lw`\) Perimeter: \(`2(l+w)`\) |
|
| Triangle | Area: \(`\frac{bh}{2}`\) Perimeter: \(`a+b+c`\) |
|
| Circle | Area: \(`πr^2`\) Circumference:
\(`2πr`\) or \(`πd`\) |
|
| Trapezoid | Area: \(` \frac{(a+b)h}{2}`\) Perimeter: \(`a+b+c+d`\) |
3D Geometry Equations
| 3D Object | Formula | Picture |
|---|---|---|
| Rectangular Prism | Volume: \(`lwh`\) SA: \(`2(lw+lh+wh)`\) |
|
| Square Based Pyramid | Volume: \(`\frac{1}{3} b^2 h`\) SA:
\(`2bs+b^2`\) |
|
| Sphere | Volume: \(`\frac{4}{3} πr^3`\) SA:
\(`4πr^2`\) |
|
| Cone | Volume: \(` \frac{1}{3} πr^2 h`\) SA: \(`πrs+πr^2`\) |
|
| Cylinder | Volume: \(`πr^2h`\) SA: \(`2πr^2+2πh`\) |
|
| Triangular Prism | Volume: \(`ah+bh+ch+bl`\) SA: \(` \frac{1}{2} blh`\) |
Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)
2D Objects
| Shape | Maximum Area | Minimum Perimeter |
|---|---|---|
| 4-sided rectangle | A rectangle must be a square to maximaze
the area for a given perimeter. The length is equal to the
width \(`A = lw`\) \(`A_{max} = (w)(w)`\) \(`A_{max} = w^2`\) |
A rectangle must be a square to minimaze
the perimeter for a given area. The length is equal to the
width. \(`P = 2(l+w)`\) \(`P_{min} = 2(w + w)`\) \(`P_{min} = 2(2w)`\) \(`P_{min} = 4w`\) |
| 3-sided rectangle | \(`l =
2w`\) \(`A = lw`\) \(`A_{max} = 2w(w)`\) \(`A_{max} = 2w^2`\) |
\(`l =
2w`\) \(`P = l+2w`\) \(`P_{min} = 2w+2w`\) \(`P_{min} = 4w`\) |
3D Objects
| 3D Object | Maximum Volumne | Minimum Surface Area |
|---|---|---|
| Cylinder(closed-top) | The cylinder must be similar to a cube
where \(`h = 2r`\) \(`V = πr^2h`\) \(`V_{max} = πr^2(2r)`\) \(`V_{max} = 2πr^3`\) |
The cylinder must be similar to a cube
where \(`h = 2r`\) \(`SA = 2πr^2+2πrh`\) \(`SA_{min} = 2πr^2+2πr(2r)`\) \(`SA_{min} = 2πr^2+4πr^2`\) \(`SA_{min} = 6πr^2`\) |
| Rectangular Prism(closed-top) | The prism must be a cube, where \(`l = w = h`\) \(`V = lwh`\) \(`V_{max} = (w)(w)(w)`\) \(`V_{max} = w^3`\) |
The prism must be a cube, where \(`l = w = h`\) \(`SA = 2lh+2lw+2wh`\) \(`SA_{min} = 2w^2+2w^2+2w^2`\) \(`SA_{min} = 6w^2`\) |
| Cylinder(open-top) | \(`h =
r`\) \(`V = πr^2h`\) \(`V_{max} = πr^2(r)`\) \(`V_{max} = πr^3`\) |
\(`h =
r`\) \(`SA = πr^2+2πrh`\) \(`SA_{min} = πr^2+2πr(r)`\) \(`SA_{min} = πr^2+2πr^2`\) \(`SA_{min} = 3πr^2`\) |
| Square-Based Rectangular Prism(open-top) | \(`h =
\frac{w}{2}`\) \(`V = lwh`\) \(`V_{max} = (w)(w)(\frac{w}{2})`\) \(`V_{max} = \frac{w^3}{2}`\) |
\(`h =
\frac{w}{2}`\) \(`SA = w^2+4wh`\) \(`SA_{min} = w^2+4w(\frac{w}{2})`\) \(`SA_{min} = w^2+2w^2`\) \(`SA_{min} = 3w^2`\) |
Labelling
Given any polygons, labelling the vertices must always:
- use
CAPITAL LETTERS - they have to be labeled in
clockwiseorcounter-clockwisedirections
- use
For a triangle, the side lengths are labeled in
LOWERCASE LETTERSassociated to the opposite side of the vertex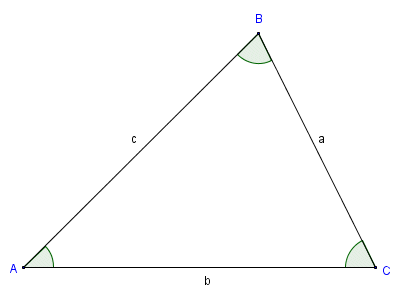
Median
Each median divides the triangle into 2 smaller triangles of equal area
The centroid is exactly \(`\dfrac{2}{3}`\)the way of each median from the vertex, or \(`\dfrac{1}{3}`\) the way from the midpoint of the opposite side, or
2:1ratio
The three medians divide the triangle into
6smaller triangles of equal area and3 pairsof congruent triangles
Terms:
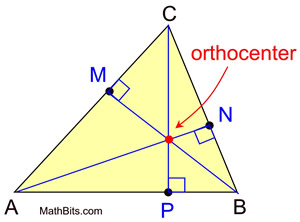
AltitudeThe height of a triangle, a line segment through a vertex and perpendicular to the opposite side
Orthocenter: where all 3 altitudes of the triangle intersectMidpoint: A point on a line where the length of either side of the point are equal
Median: A line segment joining the vertex to the midpoint of the opposite side
Midsegment: A line joining 2 midpoints of the 2 sides of a triangle
Centroid: The intersection of the 3 medians of a triangle
Proportionality theorem:
- The midsegment of a triangle is
halfthe length of the opposite side andparallelto the opposite side
- Three midsegment of a triangle divide
4 congruenttriangles with the same area
- The Ratio of the outer triangle to the triangle created by the 3
midsegments is
4 to 1
Tips
- Make sure to know your optimization formualas
- Read the word problems carefully, determine which formual to
use
- Never ASSUME, be sure to CALCULATE
as most of the time the drawings are NOT ACCURATE
- To find
missing area, take what you have, subtract what you don’t want
- Don’t be afraid to draw lines to help you solve the problem