9.4 KiB
Study Sheet
Unit 1: Functions
Words to know:
linear relationquadratic relationvertex of a parabolaline of best fitaxis of symmetry of a parabolainterceptsLinear Relation: A relation which a single straight line can be drawn through every data point and the first differences are constant
Non - Linear Relation: A single smooth curve can be drawn through every data point and the first differences are not constant
Relations
- A relation can be described using
- Table of Values (see below)
- Equations \(`(y = 3x + 5)`\)
- Graphs (Graphing the equation)
- Words
- Table of Values (see below)
- When digging into the earth, the temperature rises according to the
- following linear equation: \(`t = 15 + 0.01 h`\). \(`t`\) is the increase in temperature in
- degrees and \(`h`\) is the depth in meters.
Definitions
Parallel: 2 lines with the same slope
Perpendicular: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
Domain: The ordered set of all possible values of the independent variable \(`x`\).
Range: The ordered set of all possible values of the dependent variable \(`y`\).
Continous Data: A data set that can be broken into smaller parts. This is represented by aSolid line.
Discrete Data: A data set that cannot be broken into smaller parts. This is represented by aDashed line.
First Difference: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
Collinear Points: points that line on the same straight line
Variables
Independent Variable: A Variable in a relation which the values can be chosen or isn’t affected by anything.
Dependent Varaible: A Variable in a relation which is dependent on the independent variable.
Scatterplot and Line of Best Fit
- A scatterplot graph is there to show the relation between two
variables in a table of values.
- A line of best fit is a straight line that describes the relation
between two variables.
- If you are drawing a line of best fit, try to use as many data
points, have an equal amount of points onto and under the line of best
fit, and keep it as a straight line.

How To Determine the Equation Of a Line of Best Fit
- Find two points
ONtheline of best fit - Determine the
slopeusing the two points - Use
point-slope formto find the equation of theline of best fit
Table of values
To find first differences or any points on the line, you can use a
table of valuesIt shows the relationship between the x and y values.
Use
Finite differencesto figure out if its quadraic or linear:- If the
first differenceis constant, then its linear. (degree of 1) - If the
second differenceis constant, then its quadratic. (degree of 2)
- If the
This is a linear function
x y First difference -3 5 \(`\cdots`\) -2 7 5-7 = 2 -1 9 7-9 = 2 0 11 9-11 = 2 1 13 11-13 = 2 2 15 15-13 =2 - The difference between the first and second y values are the same as
the difference between the third and fourth. The
first differenceis constant.
- The difference between the first and second y values are the same as
the difference between the third and fourth. The
This is a quadractic function
x y First difference Second difference 5 9 \(`\cdots`\) \(`\cdots`\) 7 4 9-4 = 5 \(`\cdots`\) 9 1 4-1 = 3 5-3 = 2 11 0 1-0 = 1 3 - 1 = 2 13 1 0-1 = -1 1 -(-1) = 2 - The difference between the differences of the first and second y
values are the same as the difference of the difference between the
thrid and fourth. The
second differenceis constant.
- The difference between the differences of the first and second y
values are the same as the difference of the difference between the
thrid and fourth. The
Tips
- Label your graph correctly, the scales/scaling and always the
independent variableon thex-axisand thedependent variableony-axis
- Draw your
Line of Best Fitcorrectly
- Read the word problems carefully, and make sure you understand it
when graphing things
- Sometimes its better not to draw the shape, as it might cloud your
judgement (personal exprience)
- Label your lines
Number of Solutions
Discriminant
The discriminant determines the number of solutions (roots) there are in a quadratic equation. \(`a, b , c`\) are the
coefficients and constant of a quadratic equation: \(`y = ax^2 + bx + c`\)
\(` D = b^2 - 4ac \begin{cases} \text{2 distinct real solutions}, & \text{if } D > 0 \\ \text{1 real solution}, & \text{if } D = 0 \\ \text{no real solutions}, & \text{if } D < 0 \end{cases} `\)
Tips
- Read the questions carefully and model the system of equations
correctly
- Be sure to name your equations
- Label your lines
Definitions
Function: a relation which there is only one value of the dependent variable for each value of the independent variable (i.e, for every x-value, there is only one y-value).Vertical-line test: a test to determine whether the graph of a relation is a function. The relation is not a function if at least one vertical line drawn through the graph of the relation passes through two or more points.Real numbers: the set of real numbers is the set of all decimals - positive, negative and 0, terminating and non-terminating. This statement is expressed mathematically with the set notation \(`\{x \in \mathbb{R}\} `\)Degree: the degree of a polynomial with a single varible, say \(`x`\), is the value of the highest exponent of the variable. For example, for the polynomial \(`5x^3-4x^2+7x-8`\), the highest power or exponent is 3; the degree of the polynomial is 3.Function notation: \(`(x, y) = (x f(x))`\). \(`f(x)`\) is called function notation and represents the value of the dependent variable for a given value of the independent variable \(`x`\).Transformations: transformation are operations performed on functions to change the position or shape of the associated curves or lines.
Working with Function Notation
- Given an example of \(`f(x) = 2x^2+3x+5`\), to get \(`f(3)`\), we substitute the 3 as \(`x`\) into the function, so it now becomses \(`f(3) = 2(3)^2+3(3)+5`\).
- We can also represent new functions, the letter inside the brackets
is simply a variable, we can change it.
- Given the example \(`g(x) = 2x^2+3x+x`\), if we want \(`g(m)`\), we simply do \(`g(m) = 2m^2+3m+m`\).
Vertex Form
Vertex from: \(`f(x) = a(x-h)^2 + k`\).- \(`(-h, k)`\) is the coordinates of the vertex
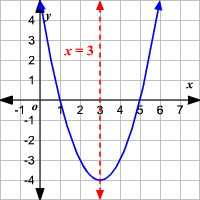
Axis of symmetry
- \(`x = -h`\)
- Example:
- \(`f(x) = 2(x-3)^2+7`\)
- \(`x = +3`\)
Direction of openning \(`\pm a`\)
- Given a quadratic in the from \(`f(x) = ax^2+bx+c`\), if \(`a > 0`\), the curve is a happy face, a smile. If \(`a < 0`\), the curve is a sad face, a sad frown.
- \(` \text{Opening} = \begin{cases} \text{if } a > 0, & \text{opens up} \\ \text{if } a < 0, & \text{opens down} \end{cases} `\)
- Examples
- \(`f(x) = -5x^2`\) opens down, sad face.
- \(`f(x) = 4(x-5)^2+7`\) opens up, happy face.
Vertical Translations \(`\pm k`\)
- \(` \text{Direction} = \begin{cases} \text{if } k > 0, & \text{UP }\uparrow \\ \text{if } k < 0, & \text{DOWN } \downarrow \end{cases} `\)
Horizontal Translations \(`\pm h`\)
\(` \text{Direction} = \begin{cases} \text{if } -h > 0, & \text{shift to the right} \\ \text{if } -h < 0, & \text{shift to the left} \end{cases} `\)
\(`f(x) = 1(x-4)^2`\)
- \(`\uparrow`\) congruent to \(`f(x) = x^2`\)
Vertical Stretch/Compression
\(`|a|\leftarrow`\): absolute bracket.
- simplify and become positive
\(` \text{Stretch/Compression} = \begin{cases} \text{if } |a| > 1, & \text{stretch by a factor of } a \\ \text{if } 0 < |a| < 1, & \text{compress by a factor of } a \end{cases} `\)
- (Multiply all the y-values from \(`y = x^2`\) by a)
- (Not congruent to \(`f(x) = x^2`\))
Example of stretching
- \(`f(x) = 2x^2`\) -Vertically stretch by a factor of 2
x y -3 9 (2)= 18-2 4 (2)= 8-1 1 (2)= 20 0 (2)= 01 1 (2)= 22 4 (2)= 83 9 (2)= 18- All y-values from \(`f(x) =x^2`\) are now multiplied by 2 to create \(`f(x)=2x^2`\)
Example of compression
- \(`f(x) = \frac{1}{2}x^2`\)
- Verticallyc ompressed by a factor of \(`\frac{1}{2}`\)
x y -3 9\(`(\frac{1}{2})`\) = 4.5 -2 4\(`(\frac{1}{2})`\) = 2 -1 1\(`(\frac{1}{2})`\) = \(`\frac{1}{2}`\) 0 0\(`(\frac{1}{2})`\) = 0 1 1\(`(\frac{1}{2})`\) = 1 2 4\(`(\frac{1}{2})`\)= \(`\frac{1}{2}`\) 3 9\(`(\frac{1}{2})`\) = 4.5 - All y-values from \(`f(x) = x^2`\) are now multiplied by \(`\frac{1}{2}`\) to create \(`f(x) = \frac{x^2}{2}`\)
- \(`f(x) = \frac{1}{2}x^2`\)