highschool/Grade 9/Math/MPM1DZ/Unit 2: Polynomials.md

Unit 2: Polyomials

Introduction to Polynomials

• A variable is a letter that represents one or more numbers
  
• An algebraic expression is a combination of variables and constants (e.g. $`x+y+6, y + 8`$)
  
• When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
  ## Methods to solve a polynomial
  1. Combine like terms
  2. Dividing polynomials
  3. Multiplying polynomials

Simplifying Alegebraic Expressions

• An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.

Factoring

• Two methods of solving; decomposition and criss-cross.
• First of all, the polynomial must be in the form of a quadratic equation ($`ax^2 + bx + c`$).
• As well, simplify the polynomial, so that all common factors are outside (e.g $`5x + 10 = 5(x + 2) )`$.

Type of Polynomial	Definition
Monomial	Polynomial that only has one term
Binomial	Polynomial that only has 2 terms
Trinomial	polynomial that only has 3 terms

Type	Example
Perfect Square Trinomials	$`(a+b)^2 = a^2+2ab+b^2 or (a-b)^2 = a^2-2ab+b^2`$
Difference with Squares	$`a^2-b^2 = (a+b)(a-b)`$
Simple Trinomials	$`x^2+6x-7 = (x+7)(x-1)`$
Complex Trinomials	$`2x^2-21x-11 = (2x+1)(x-11)`$
Common Factor	$`2ab+6b+4 = 2(ab+3b+2)`$
Factor By Grouping	$`ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)`$

Shortcuts

• 

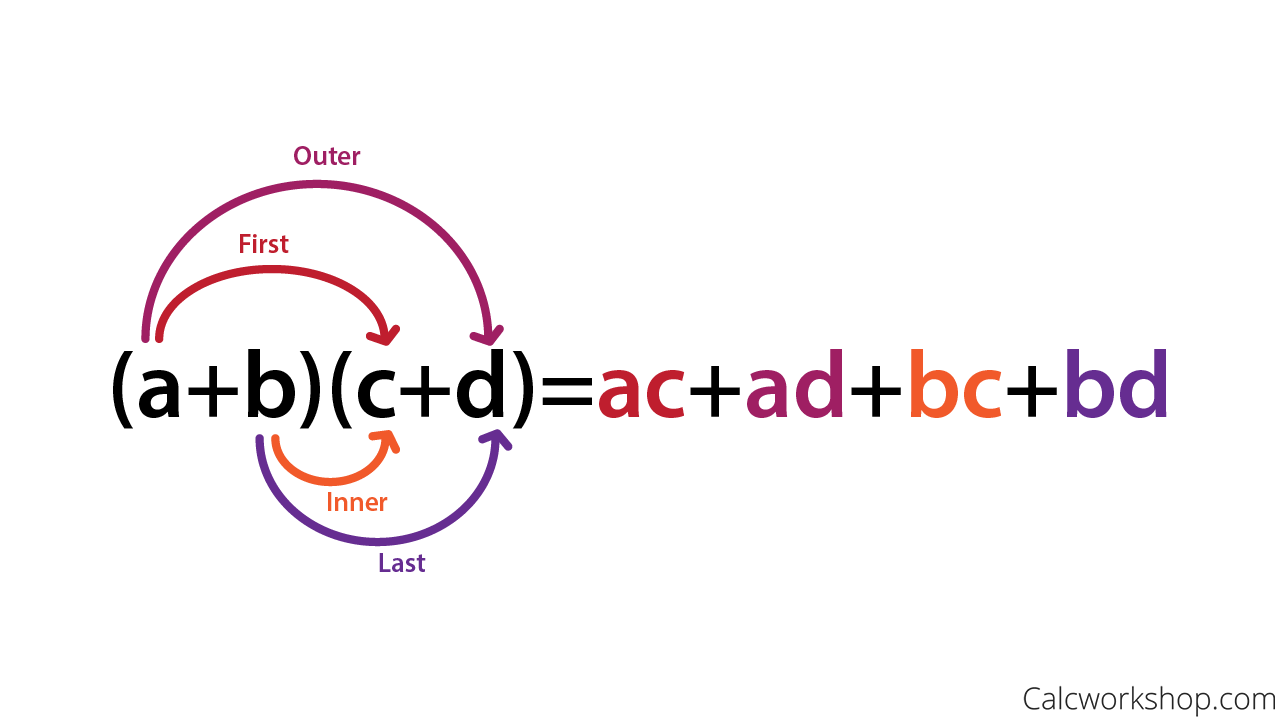
Foil / Rainbow Method

• 

Definitions

• Term a variable that may have coefficient(s) or a constant
  
• Alebraic Expressions: made up of one or more terms
  
• Like-terms: same variables raised to the same exponent

Tips

• Be sure to factor fully
  
• Learn the criss-cross (not mandatory but its a really good method to factor quadratics)
  
• Learn long division (not mandatory but its a really good method to find factors of an expression)
  
• Remember your formulas
  
• Simplify first, combine like terms