5.1 KiB
Unit 1: Analytical Geometry
- The slope of perpedicular lines are
negative reciprocal. - The slopes of parallel lines are
the same - The slope of a vertical line is
undefined - The slope of a horizontal line is
0. - The general equation of a line in standard form is \(`ax+by+c=0`\), where \(`a,b,c \in \mathbb{Z}, a>0`\)
Radius: The distance from the centre of a circle to a point on the circumference of the cricle.Diameter: the distance across a circle measured through the centreChord: a line segment joining two points on a curveCircle: a set of points in the plane which are equidistant (same distance) from the centre
Distance Formula
The distance between points \(`A(x_1, y_1)`\) and \(`B(x_2, y_2)`\) in the cartesian plane is:
\(`d = \sqrt{x^2 + y^2}`\)
\(`d = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}`\)
Identifying Types of Traingles
| Triangle | Property |
|---|---|
| Equilateral | 3 equal sides. Each angle is 60 degrees. Can’t be right angled |
| Isoceles | 2 equal sides, 2 equal angles. May be right angled |
| Scalene | No equal sides. No equal angles. May be right angled |
Pythagorean Theorem Relationships
| Formula | Statement |
|---|---|
| \(`c^2 = a^2+b^2`\) | The triangle must be right angled |
| \(`c^2 < a^2 + b^2`\) | The triangle is acute |
| \(`c^2 > a^2 + b^2`\) | The triangle is obtuse |
Equation Of A Circle With Centre \(`(0, 0)`\)
Let \(`P(x, y)`\) be any point on the circle, and \(`O`\) be the origin \(`(0, 0)`\).
Using Pythagorean Theorem,
\(`x^2+ y^2 = OP^2`\)
But, \(`OP = r`\)
\(`\therefore x^2 + y^2 = r^2`\) is the equation of a circle with centre \(`(0, 0)`\) and radius, \(`r`\).
Note: the coordinates of any point not on the cricle do not satisfy this equation
Semi-Cricle With Radius \(`r`\), And Centre \(`(0, 0)`\)
If we solve for \(`y`\) in the above equation \(`y = \pm \sqrt{r^2-x^2}`\) - \(`y = +\sqrt{r^2-x^2}`\) is the top half of the circle. - \(`y = -\sqrt{r^2-x^2}`\) is the bottom half of the circle
Equation Of A Circle With Centre \(`(x, y)`\)
Let \(`x_c, y_c`\) be the center
\(`(x - x_c)^2 + (y - y_c)^2 = r^2`\)
To get the center, just find a \(`x, y`\) such that \(`x - x_c = 0`\) and \(`y - y_c = 0`\)
Triangle Centers
Centroid
The centroid of a triangle is the common intersection of the 3 medians. The centroid is also known as the centre of mass or centre of gravity of an object (where the mass of an object is concentrated).

Procedure To Determine The Centroid
- Find the equation of the two median lines. The median is the line segment from a vertex to the midpoint of the opposite side.
- Find the point of intersection using elimination or substitution.
- Alternatively, only for checking your work, let the centroid be the point \(`(x, y)`\), and the 3 other points be \(`(x_1, y_1), (x_2, y_2), (x_3, y_3)`\) respectively, then the centroid is simply at \(`(\dfrac{x_1 + x_2 + x_3}{3}, \dfrac{y_1+y_2+y_3}{3})`\)
Circumcentre
The circumcentre (\(`O`\)) of a triangle is the common intersection of the 3 perpendicular bisectors of the sides of a triangle.
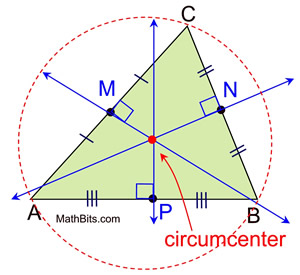
Procedure To Determine The Centroid
- Find the equation of the perpendicular bisectors of two sides. A perpendicular (right) bisector is perpendicular to a side of the triangle and passes through the midpoint of that side of the triangle.
- Find the point of intersection of the two lines using elimination or substitution.
Orthocentre
The orthocenter of a triangle is the common intersection of the 3 lines containing the altitudes.

Procedure To Determine The Orthocentre
- Find the equation of two of the altitude lines. An altitude is a perpendicular line segment from a vertex to the line of the opposite side.
- Find the point of intersection of the two lines using elimination or substitution.
Classifying Shapes

Properties Of Quadrilaterals

Ratios
- To calculate each segment of the line given the ratio, the answer is simply
- \(`(x_1 + \dfrac{p(x_2 - x_1)}{r}, y_1 + \dfrac{p(y_2 - y_1)}{r})`\), where \(`r, (x_1,y_1) (x_2,y_2), p`\) are the total ratio, first point, second point and the amount of steps respectively.
- Note that the above is for moving up a line. When moving down from the upper point, we simply subtract like so:
- \(`(x_2 - \dfrac{p(x_2 - x_1)}{r}, y_2 - \dfrac{p(y_2 - y_1)}{r})`\)
Shortest Distance From Point To a Line
- The shortest distance is always a straightline, thus, the shortest distance from a point to a line must be perpendicular.
- Thus, you can mind the slope of the line, then get the negative reciprocal (perpendicular slope), then find the equation of the perpendicular line.
- After you have the 2 lines, proceed by using subsitution or elimination to find the point of intersection.
- Then apply distance formula to find the shortest distance.