highschool/Grade 9/Math.md

Math Study Sheet!!!!

Exam Detail

Unit	Marks
Unit 1	10
Unit 2	10
Unit 3	9
Unit 4	11
Unit 5	11
Unit 6	8
Forms	4
Total	63

Section	Marks
Knowledge	21
Application	23
Thinking	12
Communication	3
Forms	4

Part	Question
A	9 multiple choice
B	10 Short Answer –> - 7 Knowledge questions - 3 Application Questions
C	10 Open Response –> - 10 Knowledge Questions - 5 Application Questions - 3 Thinking Questions - 1 Communication Question

Essential Skills (1)

Simple Arithmetics

Addition / Subtraction

Expression	Equivalent
a + b	a + b
(-a) + b	b - a
a + (-b)	a - b
(-a) + (-b)	-(a + b)
a - b	a - b
a - (-b)	a + b
(-a) -(-b)	(-a) + b

Multiplication / Division

Signs	Outcome
a * b	Positive
(-a) * b	Negative
a * (-b)	Negative
(-a) * (-b)	Positive

BEDMAS / PEMDAS

Follow BEDMAS for order of operations if there are more than one operation

Letter	Meaning
B / P	Bracket / Parentheses
E	Exponent
D	Divison
M	Multiplication
A	Addition
S	Subtraction

Interval Notation

A notation that represents an interval as a pair of numbers.
The numbers in the interval represent the endpoint. E.g. [x > 3, x ∈ R]
| means such that
E or ∈ means element of
N represents Natural Numbers (N = {x | x > 0, x ∈ Z})
W represents Whole Numbers (W = {x | x ≥ 0, x ∈ Z}) Z represents Integers (Z = {x | -∞ ≤ x ≤ ∞, x ∈ Z})
Q represents Rational Numbers (Q = {^a⁄_b |a, b ∈ Z, b ≠ 0})

Symbol	Meaning
(a, b)	Between but not including a or b, you also use this for ∞
[a, b]	Inclusive
a ∪ b	Union (or)
a ∩ b	Intersection (and)

Pythgorean Theorem

a and b are the two legs of the triangle or two sides that form a 90 degree angle of the triangle, c is the hypotenuse
a² + b² = c²

Operations with Rationals

Q = { | a, b ∈ Z, b ≠ 0 }

Any operations with rationals, there are 2 sets of rules
> 1. Rules for operations with integers > 2. Rules for operations with fractions

To Add / subtract rationals, find common denominator and then add / subtract numerator
To Multiply rationals, first reduce the fraction to their lowest terms, then multiply numerators and denominators
To Divide rationals, multiply them by the reciprocal

Example Simplify Fully:

[Reduce to lowest terms]

[Multiply by reciprocal]

[Leave as an improper fraction]

Shortcut for multiplying fractions

cross divide to keep your numbers small
Example:

Exponent Laws

Rule	Description	Example
Product	am × an = an+m	23 × 22 = 25
Quotient	am ÷ an = an-m	34 ÷ 32 = 32
Power of a Power	(am)n = amn	(23)2 = 26
Power of a Quotient	=	=
Zero as Exponents	a0 = 1	210 = 1
Negative Exponents	a-m =	1-10 =
Rational Exponents	an/m =	=

Note:
Exponential Form –> Expanded Form
6⁴ = 6 × 6 × 6 × 6

Scientific Notation

They convey accuracy and precision. It can either be written as its original number or in scientific notation: 555 (Exact) or 5.55 x 10² (3 significant figures).
In scientific notation, values are written in the form a(10ⁿ), where a is a number within 1 and 10 and n is any integer. Some examples include the following: 5.4 x 10³, 3.0 x 10², and 4.56 x 10^-4.
When the number is smaller than 1, a negative exponent is used, when the number is bigger than 10, a positve exponent is used

Remember: For scientific notation, round to 3 significant digits

Rates, Ratio and Percent

Ratio: A comparison of quantities with the same unit. These are to be reduced to lowest terms.
Examples: a:b, a:b:c, a/b, a to b

Rates: A comparison of quantities expressed in different units.
Example: 10km/hour

Percent: A fraction or ratio in which the denominator is 100
Examples: 50%, 240/100

Number Lines

a line that goes from a point to another point, a way to visualize set notations and the like

A solid filled dot is used for [] and a empty dot is used for ()

Tips

Watch out for the +/- signs
Make sure to review your knowledge of the exponent laws
For scientific notation, watch out for the decimal point Use shortcut when multiplying fractions

Polyomials (2)

Introduction to Polynomials

A variable is a letter that represents one or more numbers
An algebraic expression is a combination of variables and constants (e.g. x+y+6. y + 8)
When a specific value is assigned to a variable in a algebraic expression, this is known as substitution.
## Methods to solve a polynomial 1. Combine like terms 2. Dividing polynomials 3. Multiplying polynomials

Simplifying Alegebraic Expressions

An algebraic expression is an expression with numbers, variables, and operations. You may expand or simplify equations thereon.

Factoring

Two methods of solving; decomposition and criss-cross. First of all, the polynomial must be in the form of a quadratic equation (ax² + bx + c). As well, simplify the polynomial, so that all common factors are outside
(e.g 5x + 10 = 5(x + 2) ).

Type of Polynomial	Definition
Monomial	Polynomial that only has one term
Binomial	Polynomial that only has 2 terms
Trinomial	polynomial that only has 3 terms

Type	Example
Perfect Square Trinomials	(a+b)2 = a2+2ab+b2 or (a-b)2 = a2-2ab+b
Difference with Squares	a2-b2 = (a+b)(a-b)
Simple Trinomials	x2+6x-7 = (x+7)(x-1)
Complex Trinomials	2x2-21x-11 = (2x+1)(x-11)
Common Factor	2ab+6b+4 = 2(ab+3b+2)
Factor By Grouping	ax+ay+bx+by = (ax+ay)+(bx+by) = a(x+y)+b(x+y) = (a+b)(x+y)

Shortcuts

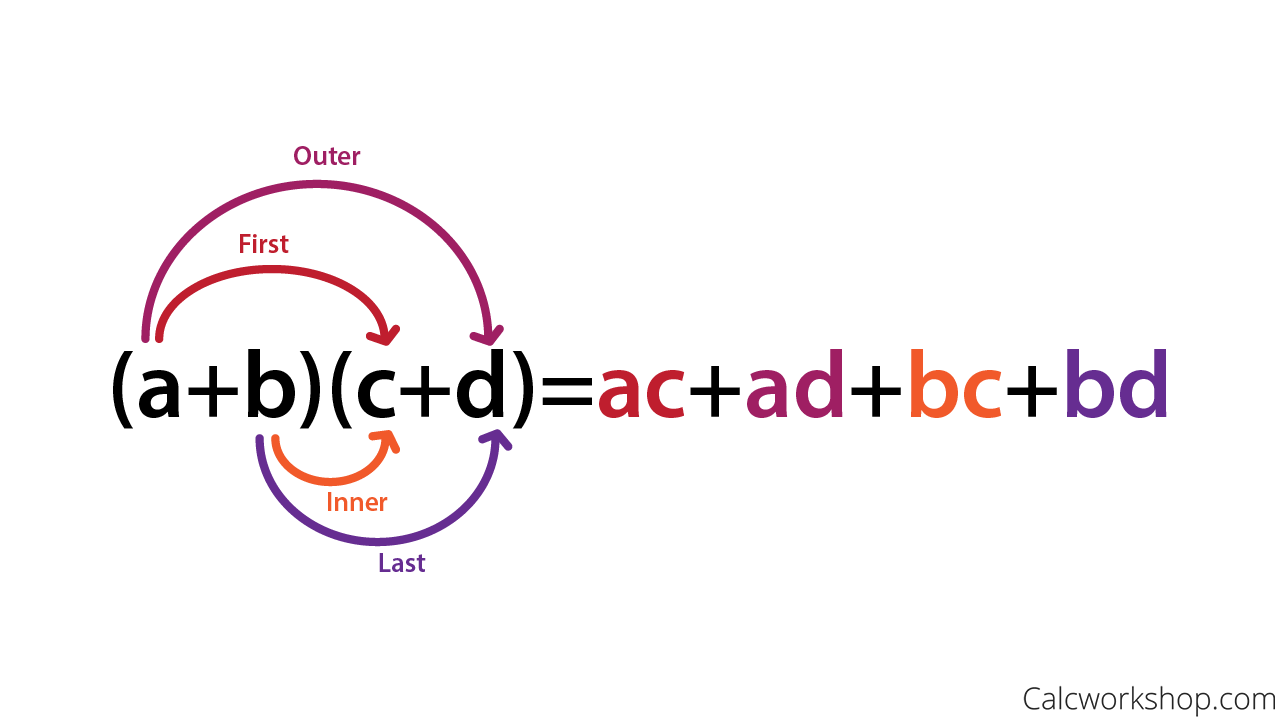
Foil / Rainbow Method

Definitions

Term a variable that may have coefficient(s) or a constant
Alebraic Expressions: made up of one or more terms
Like-terms: same variables raised to the same exponent

Tips

Be sure to factor fully
Learn the criss-cross (not mandatory but its a really good method to factor quadratics)
Learn long division (not mandatory but its a really good method to find factors of an expression)
Remember your formulas
Simplify first, combine like terms

Solving Equations and Inequailties (3)

Equations

a mathematical statement in which the value on the left side equals the value on the right side of the equal sign
To solve and equation is to find the variable that makes the statement true ### Methods to solve an equation > 1. Expand and simplify both sides > 2. Isolate using reverse order of operations > 3. Check the solution by plugging the variable back into the equation and check if the left side equals the right side

Absolute Values

There are 2 cases. For this sort of equation, you must split the equation into 2 separate equations. One of the equations will have the absolute bracket be positive while the other negative.
Absolute values are written in the form | x | where
if x > 0, | x | = x
if x = 0, | x | = 0
if x < 0, | x | = -x

Quadractic Equations

Quadratic Function: A parabolic graph where the axis of symmetry is parallel to the y-axis
Quadratic Equation: This function is set equal to 0. The solution to the equation are called roots
Solve quadratic equation by:
1. Isolation
a(x+b)² + k = 0 2. Factor using zero-product property
The Zero Factor Property refers to when a×b=0, then either a=0 or b=0.
(x-a)(x-b)=0
x = a, b

Note:
√x² = ± x (There are 2 possible solutions) Distrubutive Property - This is opening the bracket. a(x+y) = ax+ay

Tips

Absolute Values can have 2 solutions
Quadratics can also have 2 solutions
Make sure to do the reverse when moving things to the other side, meaning a positive on the left side becomes a negative on the right side

Measurement and Geometry (4)

Angle Theorems

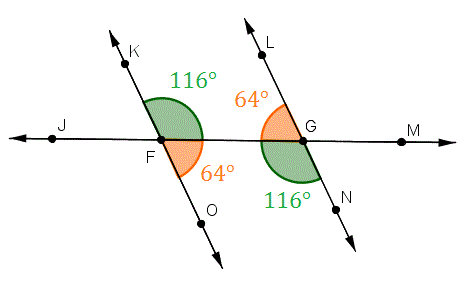
1. Transversal Parallel Line Theorems (TPT)
   

1. Alternate Angles are Equal (Z-Pattern)
   
2. Corresponding Angles Equal (F-Pattern)
   
3. Interior Angles add up to 180 (C-Pattern)

2. Supplementary Angle Triangle (SAT)
   

• When two angles add up to 180 degrees

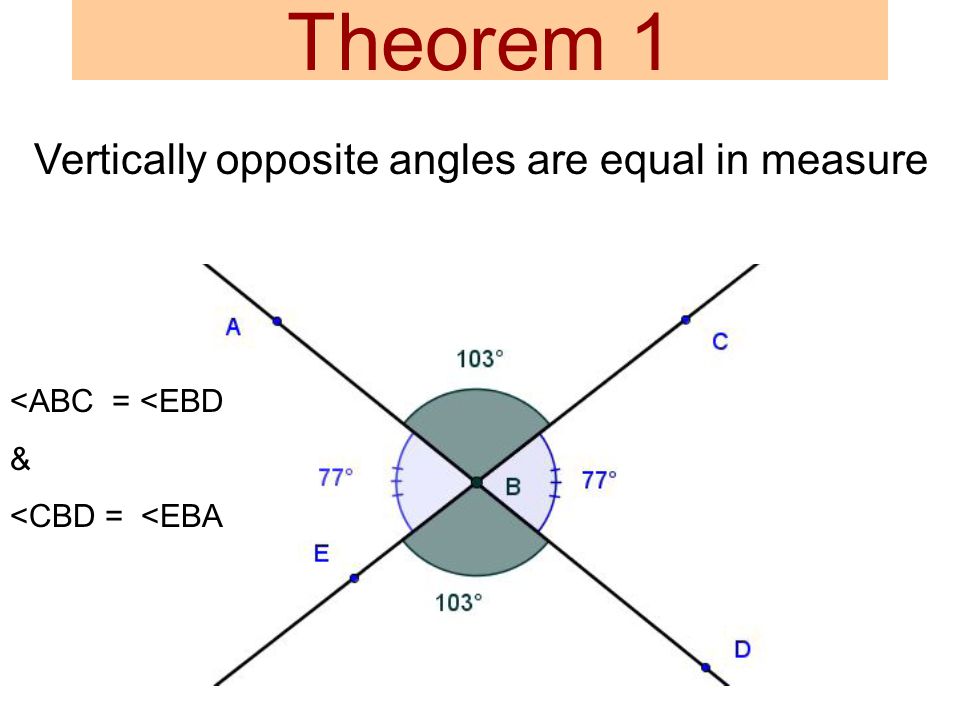
3. Opposite Angle Theorem (OAT) (OAT)
   

• Two lines intersect, two angles form opposite. They have equal measures

4. Complementary Angle Theorem (CAT)
   

• The sum of two angles that add up to 90 degrees

5. Angle Sum of a Triangle Theorem (ASTT)
   

• The sum of the three interior angles of any triangle is 180 degrees

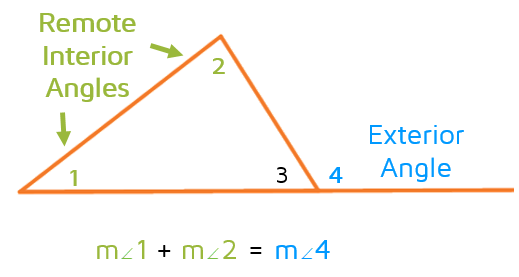
6. Exterior Angle Theorem (EAT)

• The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles

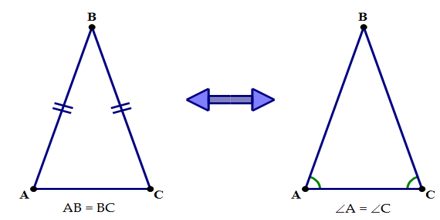
7. Isosceles Triangle Theorem (ITT)
   

• The base angles in any isosceles triangle are equal

8. Sum of The Interior Angle of a Polygon

• The sum of the interioir angles of any polygon is 180(n-2) or 180n - 360, where n is the number of sides of the polygon

9. Exterior Angles of a Convex Polygon

• The sum of the exterior angle of any convex polygon is always 360 degrees

Properties of Quadrilaterals

Determine the shape using the properties of it

Figure	Properties
Scalene Triangle	no sides equal
Isosceles Triangle	two sides equal
Equilateral Triangle	All sides equal
Right Angle Triangle	Two sides are perpendicular to each other
Parallelogram	Opposite sides are parallel and have equal length. Additionally, the diagonals bisect each other
Rectangle	Adjacent sides are perpendicular to each other. Furthermore, the diagonals bisect each other and are equal in length
Square	All sides are equal in length. The adjacent sides and diagonals are perpendicular. The adjacent sides are equal in length, so as the diagonals
Rhombus	Opposite sides are parallel and all sides are equal to each other, the diagonals are perpendicular
Trapezoid	There is one pair of opposite sides and they are parallel and unequal in length
Kite	The diagonals are perpendicular

2D Geometry Equations

Shape	Formula	Picture
Rectangle	Area: lw Perimeter: 2(l+w)
Triangle	Area: bh/2 Perimeter: a+b+c
Circle	Area: πr2 Circumference: 2πr or πd
Trapezoid	Area: (a+b)h/2 Perimeter: a+b+c+d

3D Geometry Equations

3D Object	Formula	Picture
Rectangular Prism	Volume: lwh SA: 2(lw+lh+wh)
Square Based Pyramid	Volume: 1⁄3b2h SA: 2bs+b2
Sphere	Volume: 4⁄3πr3 SA: 4πr2
Cone	Volume: 1⁄3πr2h SA: πrs+πr2
Cylinder	Volume: πr2h SA: 2πr2+2πh
Triangular Prism	Volume: ah+bh+ch+bl SA: 1⁄2blh

Optimization (For Maximimizing Area/Volume, or Minimizing Perimeter/Surface Area)

2D Objects

Shape	Maximum Area	Minimum Perimeter
4-sided rectangle	A rectangle must be a square to maximaze the area for a given perimeter. The length is equal to the width A = lw Amax = (w)(w) Amax = w2	A rectangle must be a square to minimaze the perimeter for a given area. The length is equal to the width. P = 2(l+w) Pmin = 2(w)(w) Pmin = 2(2w) Pmin = 4w
3-sided rectangle	l = 2w A = lw Amax = 2w(w) Amax = 2w2	l = 2w P = l+w2 Pmin = 2w+2w Pmin = 4w

3D Objects

3D Object	Maximum Volumne	Minimum Surface Area
Cylinder(closed-top)	The cylinder must be similar to a cube where h = 2r V = πr2h Vmax = πr2(2r) Vmax = 2πr2	The cylinder must be similar to a cube where h = 2r SA = 2πr2+2πrh SAmin = 2πr2+2πr(2r) SAmin = 2πr2+4πr2 SAmin = 6πr2
Rectangular Prism(closed-top)	The prism must be a cube, where l = w = h V = lwh Vmax = (w)(w)(w) Vmax = w3	The prism must be a cube, where l = w = h SA = 2lh+2lw+2wh SAmin = 2w2+2w2+2w2 SAmin = 6w2
Cylinder(open-top)	h = r V = πr2h Vmax = πr2(r) Vmax = πr3	h = r SA = πr2+2πrh SAmin = πr2+2πr(r) SAmin = πr2+2πr2 SAmin = 3πr2
Square-Based Rectangular Prism(open-top)	h = w/2 V = lwh Vmax = (w)(w)(w⁄2) Vmax = w3⁄2	h = w/2 SA = w2+4wh SAmin = w2+4w(w⁄2) SAmin = w2+2w2 SAmin = 3w2

Labelling

Given any polygons, labelling the vertices must always:
1. use CAPITAL LETTERS 2. they have to be labeled in clockwise or counter-clockwise directions
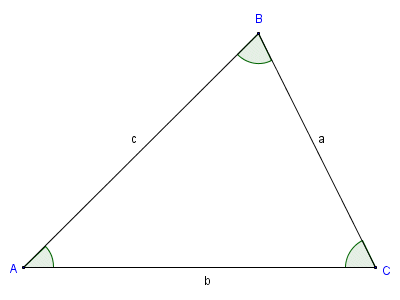
For a triangle, the side lengths are labeled in LOWERCASE LETTERS associated to the opposite side of the vertex

Median

Each median divides the triangle into 2 smaller triangles of equal area
The centroid is exactly the way of each median from the vertex, or the way from the midpoint of the opposite side, or 2:1 ratio
The three medians divide the triangle into 6 smaller triangles of equal area and 3 pairs of congruent triangles

Terms:

Altitude The height of a triangle, a line segment through a vertex and perpendicular to the opposite side
Orthocenter: where all 3 altitudes of the triangle intersect
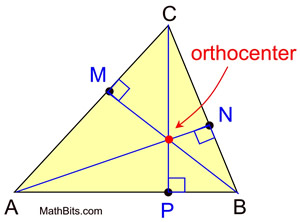
> Midpoint: A point on a line where the length of either side of the point are equal
Median: A line segment joining the vertex to the midpoint of the opposite side
Midsegment: A line joining 2 midpoints of the 2 sides of a triangle
Centroid: The intersection of the 3 medians of a triangle
>

Proportionality theorem:

The midsegment of a triangle is half the length of the opposite side and parallel to the opposite side
Three midsegment of a triangle divide 4 congruent triangles with the same area
The Ratio of the outer triangle to the triangle created by the 3 midsegments is 4 to 1

Tips

Make sure to know your optimization formualas
Read the word problems carefully, determine which formual to use
Never ASSUME, be sure to CALCULATE as most of the time the drawings are NOT ACCURATE
To find missing area, take what you have, subtract what you don’t want
Don’t be afraid to draw lines to help you solve the problem

Analytical Geometry and Linear Relations (5)

Linear Relation: A relation which a single straight line can be drawn through every data point and the first differences are constant
Non - Linear Relation: A single smooth curve can be drawn through every data point and the first differences are not constant
## Slope and Equation of Line
> Slope: The measure of the steepness of a line - rise / run or the rate of change
> Slope Formula: m = (y₂-y₁)/(x₂-x₁)
> Standard Form: ax + by + c = 0, a∈Z, b∈Z, c∈Z (must be integers and a must be positive)
> Y-intercept Form: y = mx + b
> Point-slope Form: y₂-y₁ = m(x₂-x₁)
> The slope of a vertical lines is undefined
> The slope of a horizontal line is 0 > Parallel lines have the same slope
> Perpendicular slopes are negative reciprocals

Relations

A relation can be described using
1. Table of Values (see below)
2. Equations (y = 3x + 5)
3. Graphs (Graphing the equation)
4. Words When digging into the earth, the temperature rises according to the following linear equation: t = 15 + 0.01 h. t is the increase in temperature in degrees and h is the depth in meters.

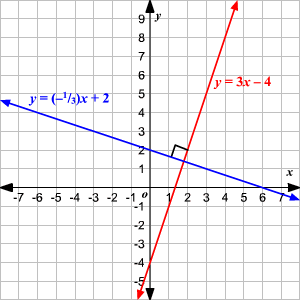
Perpendicular Lines

To find the perpendicular slope, you will need to find the slope point
Formula: slope1 × slope2 = -1
Notation: m_⊥

Definitions

Parallel: 2 lines with the same slope
Perpendicular: 2 lines with slopes that are the negative reciprocal to the other. They form a 90 degree angle where they meet.
Domain: The ordered set of all possible values of the independent variable (x).
Range: The ordered set of all possible values of the dependent variable (y).
Continous Data: A data set that can be broken into smaller parts. This is represented by a Solid line.
Discrete Data: A data set that cannot be broken into smaller parts. This is represented by a Dashed line.
First Difference: the difference between 2 consecutive y values in a table of values which the difference between the x-values are constant.
Collinear Points: points that line on the same straight line

Variables

Independent Variable: A Variable in a relation which the values can be chosen or isn’t affected by anything.
Dependent Varaible: A Variable in a relation which is dependent on the independent variable.

Statistics

Interpolation: Data inside the given data set range.
Extrapolation: Data outside the data set range.
Line of Best Fit: A line that goes through as many points as possible, and the points are the closest on either side of the line, and it represents the trend of a graph.
Coefficient of Correlation: The value that indicates the strength of two variables in a relation. 1 is the strongest and 0 is the weakest.
Partial Variation: A Variation that represents a relation in which one variable is a multiple of the other plus a costant term.

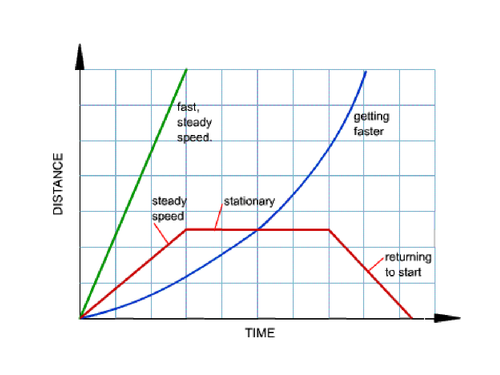
Time - Distance Graph

Time is the independent variable and distance is the dependent variable
You can’t go backwards on the x-axis, as you can’t go back in time
Plot the points accordingly
Draw the lines accordingly

Direction is always referring to:

1. go towards home
   
2. going away from home
   
3. stop

Scatterplot and Line of Best Fit

A scatterplot graph is there to show the relation between two variables in a table of values.
A line of best fit is a straight line that describes the relation between two variables.
If you are drawing a line of best fit, try to use as many data points, have an equal amount of points onto and under the line of best fit, and keep it as a straight line.

How To Determine the Equation Of a Line of Best Fit

1. Find two points ON the line of best fit
2. Determine the slope using the two points
3. Use point-slope form to find the equation of the line of best fit

Table of values

To find first differences or any points on the line, you can use a table of values

y	x	First Difference
-1	-2	…..
0	-1	(-1)-(-2) = 1
1	0	0 - (-1) = 1
2	1	1 - 0 = 1
3	2	2 - 1 = 1
4	3	3 - 2 = 1

Tips

Label your graph correctly, the scales/scaling and always the independent variable on the x-axis and the dependent variable on y-axis
Draw your Line of Best Fit correctly
Read the word problems carefully, and make sure you understand it when graphing things
Sometimes its better not to draw the shape, as it might cloud your judgement (personal exprience)
Label your lines

System of Equations (6)

Linear System

Two or more equation that you are working on all together at once on the same set of axes.
The lines may cross or intersect at a point called the Point of Intersection (POI).
The coordinated of the POI must satisfy the equation of all the lines in a linear equation.

In business, the Point of Intersection is known as the Break Even Point where Revenue - Cost = Profit
when Profit = 0. There is no gain or loss.

Number of Solutions

Discriminant

The discriminant determines the number of solutions (roots) there are in a quadratic equation. a, b, c are the coefficients and constant of a quadratic equation: y = ax<sup>2</sup> + bx + c
D = b² - 4ac
D > 0 (2 distinct real solutions)
D = 0 (1 real solution)
D < 0 (no real solutions)

Solving Linear-Quadratic Systems

To find the point of intersection, do the following:
1. Isolate both equations for y 2. Set the equations equal to each other by subsitution Equation 1 = Equation 2 3. Simplify and put everything on one side and equal to zero on the other side 4. Factor 5. Use zero-product property to solve for all possible x-values 6. Subsitute the x-values to one of the original equations to solve for all y-values 7. State a conclusion / the solution

There are 3 possible cases
In addition, to determine the number of solutions, you the Discriminant formula D = b² - 4ac

Ways to solve Systems of Equations

1. Subsitution
   Here we eliminate a variable by subbing in another variable from another equation
   We usually do this method if a variable is easily isolated
   Example:

• y = x + 10 (1) x + y + 34 = 40 (2) We can sub (1) into (2) to find x, then you the value of x we found to solve for y x + (x + 10) + 34 = 40
2x + 44 = 40
2x = -4
x = -2
  Then solve for y
y = -2 + 10
y = -8

2. Elimination Here we eliminate a variable by basically eliminate a variable from an equation
   We usually use this method first when the variables are not easily isolated, then use subsitution to solve
   Example:

•     2x + 3y = 10 (1)
      4x + 3y = 14 (2)
      ```
  We can then use elimination

  4x + 3y = 14
  2x + 3y = 10
  ------------
  2x + 0 = 4
  x = 2
  ```

  Then sub the value of x into an original equation and solve for y
2(2) + 3y = 10
3y = 6
y = 2

3. Graphing we can rewrite the equations into y-intercept form and then graph the lines, and see where the lines intersect (P.O.I), and the P.O.I is the solution

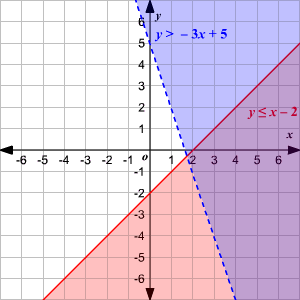
Solving Systems of Linear Inequalities

Find the intersection region as the solution.
## If:

	Use Dash line	Use Solid line
Shade the region above the line	y > mx + b	y ≥ mx + b
Shade the region below the line	y < mx + b	y ≤ mx + b

If

x > a x ≥ a

shade the region on the right

If

x < a x ≤ a

shade the region on the left

Step 1. change all inequalities to y-intercept form
Step 2. graph the line
Step 3. shade the region where all the regions overlap

Tips

Read the questions carefully and model the system of equations correctly
Be sure to name your equations
Label your lines

General Tips

Be sure to watch out for units, like cm or km
Watch out for +/-
Be sure to reverse the operation when moving things to the other side of the equation
Make sure to have a proper scale for graphs
Read question carefully and use the appropriate tools to solve
WATCH OUT FOR CARELESS MISTAKES!!!!!!!!!!!

Word Problems

Read carefully
model equations correctly
Reread the question over and over again until you fully understand it and made sure there is no tricks. :p
Lets Statement
Conclusion

Graph Problems

Look up on tips in units (5) and (6)
be sure to use a ruler when graphing

System of Equations

When in doubt or to check your work, just plug the numbers back in and check if the statement is true

Credits

Ryan Mark - He helped provide alot of information for me
Ms Hung(Katie) - She helped me check over my study sheet, an amazing teacher!
Magicalsoup - ME!