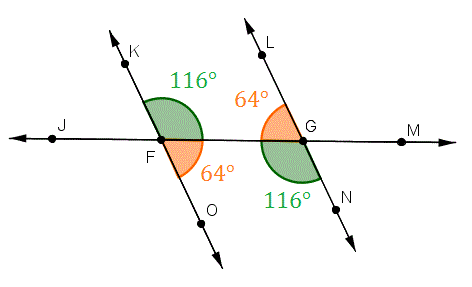
3.9 KiB
Angle Theorems
Transversal Parallel Line Theorems(TPT)- Alternate Angles are Equal
(Z-Pattern)
- Corresponding Angles Equal
(F-Pattern)
- Interior Angles add up to 180
(C-Pattern)
- Alternate Angles are Equal
Supplementary Angle Triangle(SAT)
When two angles add up to 180 degrees

Opposite Angle Theorem (OAT)(OAT)
Two lines intersect, two angles form opposite. They have equal measures
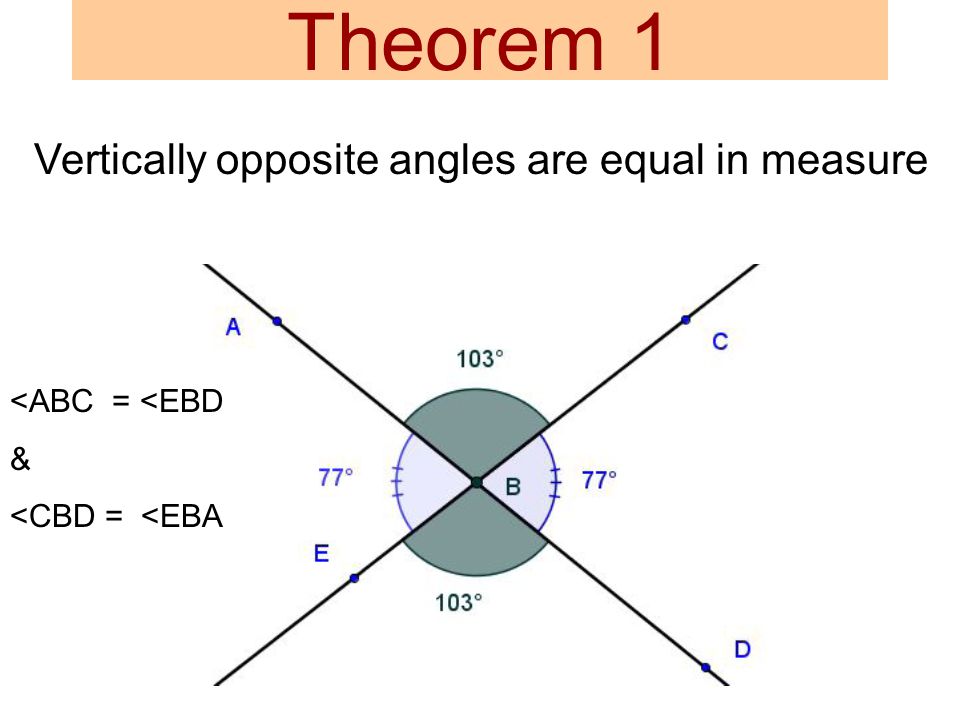
Complementary Angle Theorem(CAT)
The sum of two angles that add up to 90 degrees

Angle Sum of a Triangle Theorem(ASTT)
The sum of the three interior angles of any triangle is 180 degrees

Exterior Angle Theorem(EAT)
- The measure of an exterior angle is equal to the sum of the measures of the opposite interior angles
-
Isosceles Triangle Theorem(ITT)
The base angles in any isosceles triangle are equal

Sum of The Interior Angle of a Polygon
The sum of the interioir angles of any polygon is
180(n-2)or180n - 360, wherenis the number of sides of the polygon
Exterior Angles of a Convex Polygon
The sum of the exterior angle of any convex polygon is always
360 degrees
Congruency
Congruent: Same size and shape
Side-Side-Side (SSS)
If three sides of a triangle are respectively equal to the three sides of another triangle, then the triangles are congruent
Side-Angle-Side (SAS)
If two sides and the contained angle of a triangle are respectively equal to two sides and the contained angle of another triangle, then the triangles are congruent.
Angle-Side-Angle (ASA)
If two angles and the contained side of a triangle are respectively equal to two angles and the contained side of another triangle, then the triangles are congruent.
Similary Triangles
Similar: Same shape but different sizes (one is an
enlargement of the other)
Properties
Lets say we have \(`\triangle ABC \sim \triangle DEF`\) 1. Corresponding angles are equal - \(`\angle A = \angle D`\) - \(`\angle B = \angle E`\) - \(`\angle C = \angle F`\)
- Corresponding side are proportional.
- \(`\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF}`\)
- Proportional Area
- Let \(`k`\) be the scale factor, when concerning for triangle area, if the triangle area can be defined as \(`\dfrac{bh}{2}`\), then by using the smaller triangles side lengths our big triangle’s area is equal to \(`\dfrac{k^2bh}{2}`\). Similar equations and agruments can be dervied from this
Side-Side-Side similarity (RRR \(`\sim`\))
Three pairs of corresponding sides are in the same ratio
Side Angle Side similarity (RAR \(`\sim`\))
Two pairs of corresponding sides are proportional and the contained angle are equal.
Angle-Angle similarity (AA \(`\sim`\))
Two pairs of corresponding angles are equal.