6.1 KiB
MATH 117: Calculus 1
Functions
A function is a rule where each input has exactly one output, which can be determined by the vertical line test.
!!! definition - The domain is the set of allowable independent values. - The range is the set of allowable dependent values.
Functions can be composed to apply the result of one function to another. \[ (f\circ g)(x) = f(g(x)) \]
!!! warning Composition is not commutative: \(f\circ g \neq g\circ f\).
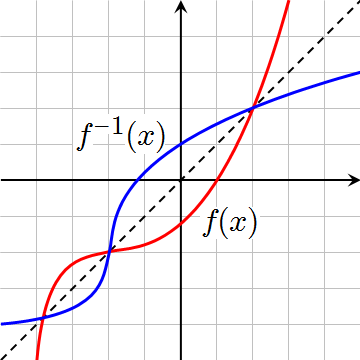
Inverse functions
The inverse of a function swaps the domain and range of the original function: \(f^{-1}(x)\) is the inverse of \(f(x)\).. It can be determined by solving for the other variable: \[ \begin{align*} y&=mx+b \\ y-b&=mx \\ x&=\frac{y-b}{m} \end{align*} \]
Because the domain and range are simply swapped, the inverse function is just the original function reflected across the line \(y=x\).
 (Source:
Wikimedia Commons, public domain)
(Source:
Wikimedia Commons, public domain)
If the inverse of a function is applied to the original function, the original value is returned. \[f^{-1}(f(x)) = x\]
A function is invertible only if it is “one-to-one”: each output must have exactly one input. This can be tested via a horizontal line test of the original function.
If a function is not invertible, restricting the domain may allow a partial inverse to be defined.
!!! example
(Source:
Wikimedia Commons, public domain) By restricting the domain to
\([0,\inf]\), the multivalued
inverse function \(y=\pm\sqrt{x}\) is reduced to just the
partial inverse \(y=\sqrt{x}\).
Symmetry
78u7u887878 An even function satisfies the property that \(f(x)=f(-x)\), indicating that it is unchanged by a reflection across the y-axis.
An odd function satisfies the property that \(-f(x)=f(-x)\), indicating that it is unchanged by a 180° rotation about the origin.
The following properties are always true for even and odd functions:
- even × even = even
- odd × odd = even
- even × odd = odd
Functions that are symmetric (that is, both \(f(x)\) and \(f(-x)\) exist) can be split into an even and odd component. Where \(g(x)\) is the even component and \(h(x)\) is the odd component: \[ \begin{align*} f(x) &= g(x) + h(x) \\ g(x) &= \frac{1}{2}(f(x) + f(-x)) \\ h(x) &= \frac{1}{2}(f(x) - f(-x)) \end{align*} \]
!!! note The hyperbolic sine and cosine are the even and odd components of \(f(x)=e^x\). \[ \cosh x = \frac{1}{2}(e^x + e^{-x}) \\ \sinh x = \frac{1}{2}(e^x - e^{-x}) \]
Piecewise functions
A piecewise function is one that changes formulae at certain intervals. To solve piecewise functions, each of one’s intervals should be considered.
Absolute value function
\[ \begin{align*} |x| = \begin{cases} x &\text{ if } x\geq 0 \\ -x &\text{ if } x < 0 \end{cases} \end{align*} \]
Signum function
The signum function returns the sign of its argument.
\[ \begin{align*} \text{sgn}(x)=\begin{cases} -1 &\text{ if } x < 0 \\ 0 &\text{ if } x = 0 \\ 1 &\text{ if } x > 0 \end{cases} \end{align*} \]
Ramp function
The ramp function makes a ramp through the origin that suddenly flatlines at 0. Where \(c\) is a constant:
\[ \begin{align*} r(t)=\begin{cases} 0 &\text{ if } x \leq 0 \\ ct &\text{ if } x > 0 \end{cases} \end{align*} \]
(Source:
Wikimedia Commons, public domain)
Floor and ceiling functions
The floor function rounds down. \[\lfloor x\rfloor\]
The ceiling function rounds up. \[\lceil x \rceil\]
Fractional part function
In a nutshell, the fractional part function:
- returns the part after the decimal point if the number is positive
- returns 1 - the part after the decimal point if the number is negative
\[\text{FRACPT}(x) = x-\lfloor x\rfloor\]
Because this function is periodic, it can be used to limit angles to the \([0, 2\pi)\) range with: \[f(\theta) = 2\pi\cdot\text{FRACPT}\biggr(\frac{\theta}{2\pi}\biggr)\]
Heaviside function
The Heaviside function effectively returns a boolean whether the number is greater than 0. \[ \begin{align*} H(x) = \begin{cases} 0 &\text{ if } t < 0 \\ 1 &\text{ if } t \geq 0 \end{cases} \end{align*} \]
This can be used to construct other piecewise functions by enabling them with \(H(x-a)\) as a factor, where \(a\) is the interval.
In a nutshell:
- \(1-H(t-a)\) lets you “turn a function off” at at \(t=a\)
- \(H(t-a)\) lets you “turn a function on at \(t=a\)
- \(H(t-a) - H(t-b)\) leaves a function on in the interval \((a, b)\)
!!! example TODO: example for converting piecewise to heaviside via collecting heavisides
and vice versaPeriodicity
The function \(f(t)\) is periodic only if there is a repeating pattern, i.e. such that for every \(x\), there is an \(f(x) = f(x + nT)\), where \(T\) is the period and \(n\) is any integer.
Circular motion
Please see SL Physics 1#6.1 - Circular motion and its subcategory “Angular thingies” for more information.
Partial function decomposition (PFD)
In order to PFD:
- Factor the denominator into irreducibly quadratic or linear terms.
- For each factor, create a term. Where capital letters below are constants:
- A linear factor \(Bx+C\) has a term \(\frac{A}{Bx+C}\).
- A quadratic factor \(Dx^2+Ex+G\) has a term \(\frac{H}{Dx^2+Ex+G}\).
- Set the two equal to each other such that the denominators can be factored out.
- Create systems of equations to solve for each constant.
!!! example To decompose \(\frac{x}{(x+1)(x^2+x+1)}\): \[ \begin{align*} \frac{x}{(x+1)(x^2+x+1)} &= \frac{A}{x+1} + \frac{Bx+C}{x^2+x+1} \\ &= \frac{A(x^2+x+1) + (Bx+C)(x+1)}{(x+1)(x^2+x+1)} \\ x &= A(x^2+x+1) + (Bx+C)(x+1) \\ 0x^2 + x + 0 &= (Ax^2 + Bx^2) + (Ax + Bx + Cx) + (A + C) \\ \\ &\begin{cases} 0 = A + B \\ 1 = A + B + C \\ 0 = A + C \end{cases} \\ A &= -1 \\ B &= 1 \\ C &= 1 \\ \\ ∴ \frac{x}{(x+1)(x^2+x+1)} &= -\frac{1}{x+1} + \frac{x + 1}{x^2 + x + 1} \end{align*} \]